平衡二叉树(AVL树)的实现
2014-05-13 15:37
288 查看
一棵AVL树是其每个节点的左子树和右子树的高度最多差1的二叉查找树(空树的高度定义为-1)。AVL树是对二叉查找树的一种改进,虽然二叉查找树平均情况下比链表的查找速度要快,但是二叉查找树也可能出现所有结点都没有左孩子(或右孩子)的情况,此时树的高度为n,这就和链表可以等价为一种数据结构,为了避免这种情况的发生,AVL树就应运而生。

第一步:结点信息
与二叉搜索树的结点信息类似,只需要添加一个树高的参数,用于插入和删除操作过程的旋转。
主要包括树的插入删除,以及保持树平衡的各种旋转操作。
辅助函数有四个:两个用于旋转操作,一个是求树高,一个是求两个值的最大值;两个是用于删除操作,分别是求某一子树的最大值和最小值的结点。
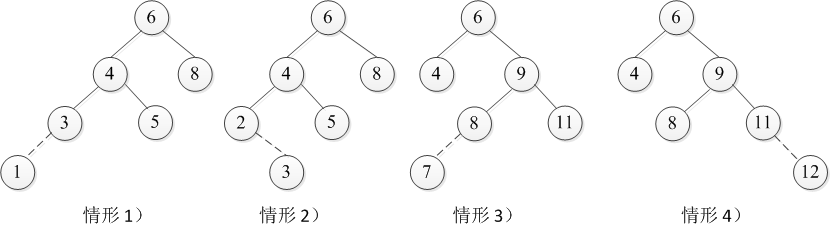
如果把必须重新平衡的结点叫k。由于任意结点最多有两个孩子,因此高度不平衡时,k点的两棵子树的高度差为2。容易看出,这种不平衡可能出现在下面四种情况中:
1)对k的左孩子的左子树进行一次插入。
2)对k的左孩子的右子树进行一次插入。
3)对k的右孩子的左子树进行一次插入。
4)对k的右孩子的右子树进行一次插入。
情形1和4是关于k点的镜像对称,而2和3是关于k点的镜像对称。因此,理论上只有两种情况,当然从编程的角度来看还是四种情况。
单旋转
对于情形1)和情形4),只需要进行一次旋转就可以恢复AVL树的平衡,以情形1)为例,阐述单旋转操作:
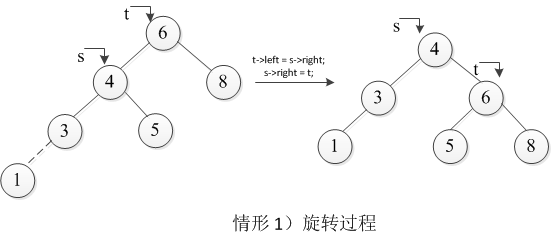
一次旋转就能恢复AVL树的平衡,不过还需要调整相应结点的height属性,并将结点s置为当前结点。这种旋转操作,就好像人为的把s结点向右旋转一次,所以该操作也叫做右旋转。
左孩子的左子树插入结点失衡——右旋转
右孩子的右子树插入结点失衡——左旋转
单旋转实现代码如下所示:
情形2)和3)稍微复杂一点,需要进行两次旋转才能恢复AVL树的平衡。以情形2)为例,阐述双旋转操作:

同样,旋转操作之后,还要修改结点的height属性值,并将q设置为当前结点。从上图可以看出,双旋转实际上就是两次简单的单旋转,所以上述操作可以通过两次单旋转函数的调用来实现。
左孩子的右子树插入结点导致不平衡——先左旋转,再右旋转
右孩子的左子树插入结点导致不平衡——先右旋转,再左旋转
双旋转的代码实现如下所示:
插入和删除操作与普通二叉搜索树一样,只是需要在插入和删除操作之后,为了保持树的平衡性,进行相应的旋转操作。
插入和删除操作的代码实现如下所示:

第一步:结点信息
与二叉搜索树的结点信息类似,只需要添加一个树高的参数,用于插入和删除操作过程的旋转。
struct AVLnode
{
T data;//结点的元素值
AVLnode *left;//指向左孩子
AVLnode *right;//指向右孩子
int height;//树高
//构造函数
AVLnode(T elem, AVLnode *l, AVLnode *r, int h=0):data(elem),left(l),right(r),height(h){}
};第二步:平衡二叉树类的声明主要包括树的插入删除,以及保持树平衡的各种旋转操作。
public://对外的接口函数
AVLTree():root(NULL){}
void insert(const T &x)//结点插入
{
insert(x, root);
}
void remove(const T &x)//结点删除
{
remove(x, root);
}
private:
AVLnode *root;//根结点
//结点插入和删除
void insert(const T &x, AVLnode * &t);
void remove(const T &x, AVLnode * &t);
//树的旋转操作
void SingleRotateLeft(AVLnode * &t);
void SingleRotateRight(AVLnode * &t);
void DoubleRotateLR(AVLnode * &t);
void DoubleRotateRL(AVLnode * &t);第三步:辅助函数辅助函数有四个:两个用于旋转操作,一个是求树高,一个是求两个值的最大值;两个是用于删除操作,分别是求某一子树的最大值和最小值的结点。
//辅助函数
int height(AVLnode * &t)
{
//结点高度,空结点的高度为-1
return t==NULL?-1:t->height;
}
int max(int a, int b)
{
return a<b?b:a;
}
AVLnode * max_node(AVLnode *t)
{
if(t)
while(t->right)
t = t->right;
return pCur;
}
AVLTree * min_node(AVLnode *t)
{
if(t)
while(t->left)
t = t->left;
return t;
}第四步:旋转如果把必须重新平衡的结点叫k。由于任意结点最多有两个孩子,因此高度不平衡时,k点的两棵子树的高度差为2。容易看出,这种不平衡可能出现在下面四种情况中:
1)对k的左孩子的左子树进行一次插入。
2)对k的左孩子的右子树进行一次插入。
3)对k的右孩子的左子树进行一次插入。
4)对k的右孩子的右子树进行一次插入。
情形1和4是关于k点的镜像对称,而2和3是关于k点的镜像对称。因此,理论上只有两种情况,当然从编程的角度来看还是四种情况。

单旋转
对于情形1)和情形4),只需要进行一次旋转就可以恢复AVL树的平衡,以情形1)为例,阐述单旋转操作:

一次旋转就能恢复AVL树的平衡,不过还需要调整相应结点的height属性,并将结点s置为当前结点。这种旋转操作,就好像人为的把s结点向右旋转一次,所以该操作也叫做右旋转。
左孩子的左子树插入结点失衡——右旋转
右孩子的右子树插入结点失衡——左旋转
单旋转实现代码如下所示:
template <typename T>
void AVLTree<T>::SingleRotateLeft(AVLnode * &t)
{
AVLnode *s = t->right;
t->right = s->left
s->left = t;
t->height = max(height(t->left), height(t->right)) + 1;
s->height = max(t->height, height(s->right)) + 1;
t = s;
}
template <typename T>
void AVLTree<T>::SingleRotateRight(AVLnode * &t)
{
AVLnode *s = t->left;
t->left = s->right;
s->right = t;
t->height = max(height(t->left), height(t->right)) + 1;
s->height = max(height(s->left), t->height);
t = s;
}双旋转情形2)和3)稍微复杂一点,需要进行两次旋转才能恢复AVL树的平衡。以情形2)为例,阐述双旋转操作:

同样,旋转操作之后,还要修改结点的height属性值,并将q设置为当前结点。从上图可以看出,双旋转实际上就是两次简单的单旋转,所以上述操作可以通过两次单旋转函数的调用来实现。
t->left = SingleRotateLeft(t->left); return SingleRotateRight(t);
左孩子的右子树插入结点导致不平衡——先左旋转,再右旋转
右孩子的左子树插入结点导致不平衡——先右旋转,再左旋转
双旋转的代码实现如下所示:
template <typename T>
void AVLTree<T>::DoubleRotateLR(AVLnode* &t)
{
AVLnode *p = t->left;
AVLnode *q = p->right;
t->left = q->right;
p->right = q->left;
q->left = p;
q->right = t;
t->height = max(height(t->left), height(t->right)) + 1;
p->height = max(height(p->left), height(p->right)) + 1;
q->height = max(p->height, t->height) + 1;
t = q;
}
template <typename T>
void AVLTree<T>::DoubleRotateRL(AVLnode* &t)
{
AVLnode *p = t->right;
AVLnode *q = p->left;
t->right = q->left;
p->left = q->right;
q->left = t;
q->right = p;
t->height = max(height(t->left), height(t->right)) + 1;
p->height = max(height(p->left), height(p->right)) + 1;
q->height = max(t->height, p->height) + 1;
t = q;
}第五步:插入和删除操作插入和删除操作与普通二叉搜索树一样,只是需要在插入和删除操作之后,为了保持树的平衡性,进行相应的旋转操作。
插入和删除操作的代码实现如下所示:
template <typename T>
void AVLTree<T>::insert(const T &x, AVLnode * &t)
{
if(!t)//找到插入点
t = new AVLnode(x, NULL, NULL);
else if(x < t->data)
{
insert(x, t->left);
if(height(t->left) - height(t->right) == 2)
{
if(x < t->left->data)//结点插在当前结点左孩子的左子树
SingleRotateRight(t);//右单旋转
else//结点插在当前结点左孩子的右子树
DoubleRotateLR(t);//先左旋再右旋
}
else//不需要调整,只需要重新计算树的高度
t->height = max(height(t->left), height(t->right)) + 1;
}
else if(x > t->data)
{
insert(x, t->right);
if(height(t->right) - height(t->left) == 2)
{
if(x > t->right->data)//结点插在当前结点右孩子的右子树
SingleRotateLeft(t);//左单旋转
else//结点插在当前结点左孩子的右子树
DoubleRotateRL(t);//先右旋再左旋
}
else//不需要调整,只需要重新计算树的高度
t->height = max(height(t->left), height(t->right)) + 1;
}
else;//不考虑重复的值
}
template <typename T>
void AVLTree<T>::remove(const T &x, AVLnode * &t)
{
if(!t)return;//找到叶结点以下,即没有要删除的结点,啥也不做
if(x < t->data)
{
remove(x, t->left);
if(height(t->right) - height(t->left) == 2)
{
AVLnode * temp = t->right;
if(height(temp->right) > height(temp->left))//类似于结点插在当前结点右孩子的右子树上
SingleRotateLeft(t);//左单旋转
else//类似结点插在当前结点右孩子的左子树
DoubleRotateRL(t);//先右旋再左旋
}
else//不需要调整,只需要重新计算树的高度
t->height = max(height(t->left), height(t->right)) + 1;
}
else if(x > t->data)
{
remove(x, t->right);
if(height(t->left) - height(t->right) == 2)
{
AVLnode * temp = t->left;
if(height(temp->left) > height(temp->right))//类似于结点插在当前结点左孩子的左子树上
SingleRotateRight(t);//右单旋转
else//类似结点插在当前结点左孩子的右子树
DoubleRotateLR(t);//先左旋再右旋
}
else//不需要调整,只需要重新计算树的高度
t->height = max(height(t->left), height(t->right)) + 1;
}
else//要删除结点等于当前结点
{
if(t->left && t->right)
//t的左右子树都非空,把remove操作转移到只有一个非空子树的结点或者叶子结点上
{
if(height(t->left) > height(t->right))
{
t->data = max_node(t->left)->data;
remove(t->data, t->left);
}
else
{
t->data = min_node(t->right)->data;
remove(t->data, t->right);
}
}
else
{
AVLnode *oldnode = t;
t = t->left?t->left:t->right;
delete oldnode;
oldnode = NULL;
}
}
}
相关文章推荐
- 数据结构——AVL树(平衡二叉树)的详细实现
- 平衡二叉树——AVL树的原理和实现
- AVL树(平衡二叉树)及其实现
- 数据结构之---C语言实现平衡二叉树(AVL树)
- java数据结构与算法之平衡二叉树(AVL树)的设计与实现
- java数据结构与算法之平衡二叉树(AVL树)的设计与实现
- 平衡二叉树(AVL树)一图一步骤代码实现左旋右旋,左右平衡操作
- PHP实现平衡二叉树(AVL树)
- AVL树 平衡二叉树 简介及实现原理
- golang实现高度平衡二叉树(AVL树)
- 平衡二叉树---AVL树的实现
- java实现AVL树(一种自平衡二叉树)数据结构
- 平衡二叉树(AVL树)的简单实现
- 平衡二叉树——AVL树的实现
- Java实现平衡二叉树(AVL树)
- 数据结构之 AVL树(平衡二叉树)(C语言实现)
- 平衡二叉树(AVL树)的简单实现
- 平衡二叉树——AVL树的实现
- 平衡二叉树(AVL树)算法 Java实现
- 平衡二叉树的实现,AVL树的实现
