POJ 3164 Command Network

链接：http://poj.org/problem?id=3164

题意：有向图的最小生成树——最小树形图。

思路：

朱刘算法

========================== 分割线之下摘自Sasuke_SCUT的blog==================================================

最 小树形图，就是给有向带权图中指定一个特殊的点root，求一棵以root为根的有向生成树T，并且T中所有边的总权值最小。最小树形图的第一个算法是 1965年朱永津和刘振宏提出的复杂度为O(VE)的算法。

判断是否存在树形图的方法很简单，只需要以v为根作一次图的遍历就可以了，所以下面的 算法中不再考虑树形图不存在的情况。

在所有操作开始之前，我们需要把图中所有的自环全都清除。很明显，自环是不可能在任何一个树形图上的。只有进 行了这步操作，总算法复杂度才真正能保证是O(VE)。

首先为除根之外的每个点选定一条入边，这条入边一定要是所有入边中最小的。现在所有的最小 入边都选择出来了，如果这个入边集不存在有向环的话，我们可以证明这个集合就是该图的最小树形图。这个证明并不是很难。如果存在有向环的话，我们就要将这 个有向环所称一个人工顶点，同时改变图中边的权。假设某点u在该环上，并设这个环中指向u的边权是in[u]，那么对于每条从u出发的边(u, i, w)，在新图中连接(new, i, w)的边，其中new为新加的人工顶点; 对于每条进入u的边(i, u, w)，在新图中建立边(i, new, w-in[u])的边。为什么入边的权要减去in[u]，这个后面会解释，在这里先给出算法的步骤。然后可以证明，新图中最小树形图的权加上旧图中被收缩 的那个环的权和，就是原图中最小树形图的权。

上面结论也不做证明了。现在依据上面的结论，说明一下为什么出边的权不变，入边的权要减去in [u]。对于新图中的最小树形图T，设指向人工节点的边为e。将人工节点展开以后，e指向了一个环。假设原先e是指向u的，这个时候我们将环上指向u的边 in[u]删除，这样就得到了原图中的一个树形图。我们会发现，如果新图中e的权w'(e)是原图中e的权w(e)减去in[u]权的话，那么在我们删除 掉in[u]，并且将e恢复为原图状态的时候，这个树形图的权仍然是新图树形图的权加环的权，而这个权值正是最小树形图的权值。所以在展开节点之后，我们 得到的仍然是最小树形图。逐步展开所有的人工节点，就会得到初始图的最小树形图了。

如果实现得很聪明的话，可以达到找最小入边O(E)，找环 O(V)，收缩O(E)，其中在找环O(V)这里需要一点技巧。这样每次收缩的复杂度是O(E)，然后最多会收缩几次呢？由于我们一开始已经拿掉了所有的 自环，我门可以知道每个环至少包含2个点，收缩成1个点之后，总点数减少了至少1。当整个图收缩到只有1个点的时候，最小树形图就不不用求了。所以我们最 多只会进行V-1次的收缩，所以总得复杂度自然是O(VE)了。由此可见，如果一开始不除去自环的话，理论复杂度会和自环的数目有关。

======================== 分割线之上摘自Sasuke_SCUT的blog=====================================================

下 面是朱刘算法的构造图



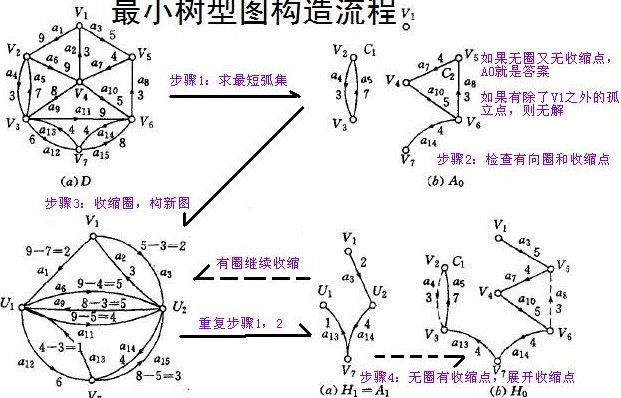
模板：http://blog.csdn.net/wsniyufang/article/details/6747406

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<queue>
#include<stack>
#include<vector>
#include<ctype.h>
#include<algorithm>
#include<string>
#define PI acos(-1.0)
#define maxn 105
#define maxm 10005
#define INF 1<<25
#define MAX 0x7fffffff
#define M 109
#define type double
typedef long long ll;
using namespace std;
const type inf=(1)<<30;
struct Node
{
int u , v;
type cost;
} E[M*M+5];
int pre[M],ID[M],vis[M],pp[M][2];
type In[M];
int n,m;
type Directed_MST(int root,int NV,int NE)
{
type ret = 0;
while(true)
{
//1.找最小入边
for(int i=0; i<NV; i++) In[i] = inf;
for(int i=0; i<NE; i++)
{
int u = E[i].u;
int v = E[i].v;
if(E[i].cost < In[v] && u != v)
{
pre[v] = u;
In[v] = E[i].cost;
}
}
for(int i=0; i<NV; i++)
{
if(i == root) continue;
if(In[i] == inf) return -1;//除了跟以外有点没有入边,则根无法到达它
}
//2.找环
int cntnode = 0;
memset(ID,-1,sizeof(ID));
memset(vis,-1,sizeof(vis));
In[root] = 0;
for(int i=0; i<NV; i++) //标记每个环
{
ret += In[i];
int v = i;
while(vis[v] != i && ID[v] == -1 && v != root)
{
vis[v] = i;
v = pre[v];
}
if(v != root && ID[v] == -1)
{
for(int u = pre[v] ; u != v ; u = pre[u])
{
ID[u] = cntnode;
}
ID[v] = cntnode ++;
}
}
if(cntnode == 0) break;//无环
for(int i=0; i<NV; i++) if(ID[i] == -1)
{
ID[i] = cntnode ++;
}
//3.缩点,重新标记
for(int i=0; i<NE; i++)
{
int v = E[i].v;
E[i].u = ID[E[i].u];
E[i].v = ID[E[i].v];
if(E[i].u != E[i].v)
{
E[i].cost -= In[v];
}
}
NV = cntnode;
root = ID[root];
}
return ret;
}
double dis(int x,int y)
{
return (pp[x][0]-pp[y][0])*(pp[x][0]-pp[y][0])+(pp[x][1]-pp[y][1])*(pp[x][1]-pp[y][1]);
}
int main()
{
int tot,tt;
while(scanf("%d%d",&tot,&tt)!=EOF)
{
for(int i=0;i<tot;i++)
scanf("%d%d",&pp[i][0],&pp[i][1]);
for(int i=0;i<tt;i++)
{
scanf("%d%d",&E[i].u,&E[i].v);
E[i].u--;
E[i].v--;
E[i].cost=sqrt(dis(E[i].u,E[i].v));
}
double ss=Directed_MST(0,tot,tt);
if(ss==-1)
printf("poor snoopy\n");
else printf("%.2lf\n",ss);
}
}