搜索与优化2优化方法总结
2013-11-17 15:10
239 查看
针对特定的模型,发现其最佳参数值的过程通常被称为优化问题。
1爬山法 (局部贪婪找到最值,局部最优解)
爬山法是一种局部搜索算法,也属一种启发式方法。但它一般只能得到局部最优,并且这种解还依赖于起始点的选取。现在有各种版本的爬山法,下面给出的是一种简单迭代爬山法。
开始时,当前解的所有可能邻域都被考虑,并且将且有最好评估值eval_r(vn)的串vn与当前串vc作比较。如果eval_r(vc)比eval_r(vn)差,则新串vn就成为当前串;否则,则没有可能再进行局部改进:该算法已经达到局部最优或者全局最优(变量local=TRUE).
在这种情况下,算法的下一次迭代(t←t+1)随机选取一个新的当前串来执行.
2梯度下降 (找最值的方法)
最陡峭下降(Steepest-Descend)
条件:函数能求导
适用范围:


我们知道,函数的曲线如下:

编程实现:c++ code
[cpp] view
plaincopy
/*
* @author:郑海波
* blog.csdn.net/nuptboyzhb/
* 2012-12-11
*/
#include <iostream>
#include <math.h>
using namespace std;
int main()
{
double e=0.00001;//定义迭代精度
double alpha=0.5;//定义迭代步长
double x=0;//初始化x
double y0=x*x-3*x+2;//与初始化x对应的y值
double y1=0;//定义变量,用于保存当前值
while (true)
{
x=x-alpha*(2.0*x-3.0);
y1=x*x-3*x+2;
if (abs(y1-y0)<e)//如果2次迭代的结果变化很小,结束迭代
{
break;
}
y0=y1;//更新迭代的结果
}
cout<<"Min(f(x))="<<y0<<endl;
cout<<"minx="<<x<<endl;
return 0;
}
//运行结果
//Min(f(x))=-0.25
//minx=1.5
3EM期望最大化 (找最值)
条件:对于一般的模型,EM算法需要经过若干次迭代才能收敛,因为在M-Step依然是采用求导函数的方法,所以它找到的是极值点,即局部最优解,而非全局最优解。也正是因为EM算法具有局部性,所以它找到的最终解跟初始值θ(0)的选取有很大关系。
在统计学中,“似然性”和“或然性”或“概率”又有明确的区分。概率用于在已知一些参数的情况下,预测接下来的观测所得到的结果,而似然性则是用于在已知某些观测所得到的结果时,对有关事物的性质的参数进行估计。
在这种意义上,似然函数可以理解为条件概率的逆反。在已知某个参数B时,事件A会发生的概率写作:

利用贝叶斯定理,

因此,我们可以反过来构造表示似然性的方法:已知有事件A发生,运用似然函数
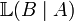
,我们估计参数B的可能性。形式上,似然函数也是一种条件概率函数,但我们关注的变量改变了:
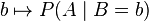
注意到这里并不要求似然函数满足归一性:

。一个似然函数乘以一个正的常数之后仍然是似然函数。对所有
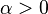
,都可以有似然函数:

主条目:最大似然估计
最大似然估计是似然函数最初也是最自然的应用。上文已经提到,似然函数取得最大值表示相应的参数能够使得统计模型最为合理。从这样一个想法出发,最大似然估计的做法是:首先选取似然函数(一般是概率密度函数或概率质量函数),整理之后求最大值。实际应用中一般会取似然函数的对数作为求最大值的函数,这样求出的最大值和直接求最大值得到的结果是相同的。似然函数的最大值不一定唯一,也不一定存在。与矩法估计比较,最大似然估计的精确度较高,信息损失较少,但计算量较大。
一个自然的想法是从这个分布中抽出一个具有

个值的采样
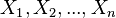
,然后用这些采样数据来估计

.
一旦我们获得

,我们就能从中找到一个关于

的估计。最大似然估计会寻找关于

的最可能的值(即,在所有可能的

取值中,寻找一个值使这个采样的“可能性”最大化)。这种方法正好同一些其他的估计方法不同,如

的非偏估计,非偏估计未必会输出一个最可能的值,而是会输出一个既不高估也不低估的

值。
要在数学上实现最大似然估计法,我们首先要定义似然函数:

并且在

的所有取值上,使这个函数最大化(一阶导数)。这个使可能性最大的

值即被称为

的最大似然估计
考虑一个抛硬币的例子。假设这个硬币正面跟反面轻重不同。我们把这个硬币抛80次(即,我们获取一个采样
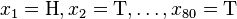
并把正面的次数记下来,正面记为H,反面记为T)。并把抛出一个正面的概率记为

,抛出一个反面的概率记为
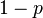
(因此,这里的

即相当于上边的

)。假设我们抛出了49个正面,31个反面,即49次H,31次T。假设这个硬币是我们从一个装了三个硬币的盒子里头取出的。这三个硬币抛出正面的概率分别为
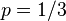
,
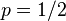
,

.这些硬币没有标记,所以我们无法知道哪个是哪个。使用最大似然估计,通过这些试验数据(即采样数据),我们可以计算出哪个硬币的可能性最大。这个似然函数取以下三个值中的一个:
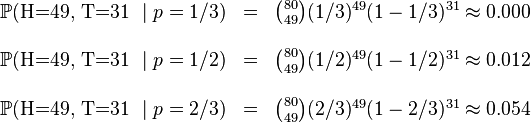
我们可以看到当

时,似然函数取得最大值。这就是

的最大似然估计。
此博客解释比较好
http://www.cnblogs.com/zhangchaoyang/articles/2623364.html
EM是一种迭代算法,它试图找到一系列的估计参数θ(0),θ(1),θ(2),....使得训练数据的marginal likelihood是不断增加的,即:

算法刚开始的时候θ(0)赋予随机的值,每次迭代经历一个E-Step和一个M-Step,迭代终止条件是θ(i+1)与θ(i)相等或十分相近。
E-Step是在θ(i)已知的情况下计算X=x时Y=y的后验概率:

f(x|X)是一个权值,它表示观测值x在所有观察结果X中出现的频率。
M-Step:

其中

在E-Step已经求出来了。这时候可以用“令一阶导数等于0”的方法求出θ'。
EM算法收敛性的证明需要用到Jensen不等式,这里略去不讲。
EM是一种迭代算法,它试图找到一系列的估计参数θ(0),θ(1),θ(2),....使得训练数据的marginal likelihood是不断增加的,即:

算法刚开始的时候θ(0)赋予随机的值,每次迭代经历一个E-Step和一个M-Step,迭代终止条件是θ(i+1)与θ(i)相等或十分相近。
E-Step是在θ(i)已知的情况下计算X=x时Y=y的后验概率:

f(x|X)是一个权值,它表示观测值x在所有观察结果X中出现的频率。
M-Step:

其中

在E-Step已经求出来了。这时候可以用“令一阶导数等于0”的方法求出θ'。
EM算法收敛性的证明需要用到Jensen不等式,这里略去不讲。
4最小二乘法(最小化误差的平方和 利用样本通过求导解方程组的方法求出评价函数平方和最小值进而确定模型参数)
条件:在研究两个变量之间的关系时,可以用回归分析的方法进行分析。当确定了描述两个变量之间的回归模型后,就可以使用最小二乘法估计模型中的参数,进而建立经验方程.
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
最小二乘法原理
在我们研究两个变量(x, y)之间的相互关系时,通常可以得到一系列成对的数据( x1, y1. x2, y2. … xm ,
ym );将这些数据描绘在x -y直角坐标系中,若发现这些点在一条直线附近,可以令这条直线方程如(式1-1)。
Y计= a0 + a1 X (式1-1)
其中:a0、a1 是任意实数
为建立这直线方程就要确定a0和a1,应用 最小二乘法原理 ,将实测值Yi与利用(式1-1)计算值(Y计=a0+a1X)的离差(Yi-Y计)的平方和〔∑(Yi -
Y计)2〕最小为“优化判据”。
令: φ = ∑(Yi - Y计)2 (式1-2)
把(式1-1)代入(式1-2)中得:
φ = ∑(Yi - a0 - a1 Xi)2 (式1-3)
当∑(Yi-Y计)平方最小时,可用函数 φ 对a0、a1求偏导数,令这两个偏导数等于零。

亦即:
m a0 + (∑Xi ) a1 = ∑Yi (式1-6)
(∑Xi ) a0 + (∑Xi2 ) a1 = ∑(Xi,
Yi) (式1-7)
得到的两个关于a0、 a1为未知数的两个方程组,解这两个方程组得出:
a0 = (∑Yi) / m - a1(∑Xi) / m (式1-8)
a1 = [m∑Xi Yi - (∑Xi ∑Yi)] / [m∑Xi2 -
(∑Xi)2 )] (式1-9)
这时把a0、a1代入(式1-1)中, 此时的(式1-1)就是我们回归的元线性方程即:数学模型。
在回归过程中,回归的关联式是不可能全部通过每个回归数据点( x1, y1. x2, y2. … xm ,
ym ),为了判断关联式的好坏,可借助相关系数“R”,统计量“F”,剩余标准偏差“S”进行判断;“R”越趋近于 1 越好;“F”的绝对值越大越好;“S”越趋近于 0 越好。
R = [∑XiYi - m (∑Xi / m)(∑Yi / m)]/ SQR{[∑Xi2 -
m (∑Xi / m)2][∑Yi2 - m (∑Yi / m)2]}
(式1-10) *
在(式1-1)中,m为样本容量,即实验次数;Xi、Yi分别任意一组实验X、Y的数值。
1爬山法 (局部贪婪找到最值,局部最优解)
爬山法是一种局部搜索算法,也属一种启发式方法。但它一般只能得到局部最优,并且这种解还依赖于起始点的选取。现在有各种版本的爬山法,下面给出的是一种简单迭代爬山法。
开始时,当前解的所有可能邻域都被考虑,并且将且有最好评估值eval_r(vn)的串vn与当前串vc作比较。如果eval_r(vc)比eval_r(vn)差,则新串vn就成为当前串;否则,则没有可能再进行局部改进:该算法已经达到局部最优或者全局最优(变量local=TRUE).
在这种情况下,算法的下一次迭代(t←t+1)随机选取一个新的当前串来执行.
| procedure 迭代爬山法 begin t ← 0 初始化 best repeat local ← FALSE 随机选取一个当前点vc 评估vc repeat 在vc的邻域中选择所有新点 从这个新点的集合中找到使评估函数eval的值最优的点vn if eval(vn) 好于 eval(vc) then vc ← vn else local ← TRUE until local t ← t+1 if vc 好于 best then best ← vc until t = MAX end |
最陡峭下降(Steepest-Descend)
条件:函数能求导
适用范围:


我们知道,函数的曲线如下:

编程实现:c++ code
[cpp] view
plaincopy
/*
* @author:郑海波
* blog.csdn.net/nuptboyzhb/
* 2012-12-11
*/
#include <iostream>
#include <math.h>
using namespace std;
int main()
{
double e=0.00001;//定义迭代精度
double alpha=0.5;//定义迭代步长
double x=0;//初始化x
double y0=x*x-3*x+2;//与初始化x对应的y值
double y1=0;//定义变量,用于保存当前值
while (true)
{
x=x-alpha*(2.0*x-3.0);
y1=x*x-3*x+2;
if (abs(y1-y0)<e)//如果2次迭代的结果变化很小,结束迭代
{
break;
}
y0=y1;//更新迭代的结果
}
cout<<"Min(f(x))="<<y0<<endl;
cout<<"minx="<<x<<endl;
return 0;
}
//运行结果
//Min(f(x))=-0.25
//minx=1.5
3EM期望最大化 (找最值)
条件:对于一般的模型,EM算法需要经过若干次迭代才能收敛,因为在M-Step依然是采用求导函数的方法,所以它找到的是极值点,即局部最优解,而非全局最优解。也正是因为EM算法具有局部性,所以它找到的最终解跟初始值θ(0)的选取有很大关系。
在统计学中,“似然性”和“或然性”或“概率”又有明确的区分。概率用于在已知一些参数的情况下,预测接下来的观测所得到的结果,而似然性则是用于在已知某些观测所得到的结果时,对有关事物的性质的参数进行估计。
在这种意义上,似然函数可以理解为条件概率的逆反。在已知某个参数B时,事件A会发生的概率写作:

利用贝叶斯定理,

因此,我们可以反过来构造表示似然性的方法:已知有事件A发生,运用似然函数
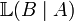
,我们估计参数B的可能性。形式上,似然函数也是一种条件概率函数,但我们关注的变量改变了:
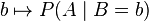
注意到这里并不要求似然函数满足归一性:

。一个似然函数乘以一个正的常数之后仍然是似然函数。对所有
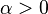
,都可以有似然函数:

最大似然估计[编辑]
主条目:最大似然估计最大似然估计是似然函数最初也是最自然的应用。上文已经提到,似然函数取得最大值表示相应的参数能够使得统计模型最为合理。从这样一个想法出发,最大似然估计的做法是:首先选取似然函数(一般是概率密度函数或概率质量函数),整理之后求最大值。实际应用中一般会取似然函数的对数作为求最大值的函数,这样求出的最大值和直接求最大值得到的结果是相同的。似然函数的最大值不一定唯一,也不一定存在。与矩法估计比较,最大似然估计的精确度较高,信息损失较少,但计算量较大。
一个自然的想法是从这个分布中抽出一个具有

个值的采样
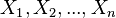
,然后用这些采样数据来估计

.
一旦我们获得

,我们就能从中找到一个关于

的估计。最大似然估计会寻找关于

的最可能的值(即,在所有可能的

取值中,寻找一个值使这个采样的“可能性”最大化)。这种方法正好同一些其他的估计方法不同,如

的非偏估计,非偏估计未必会输出一个最可能的值,而是会输出一个既不高估也不低估的

值。
要在数学上实现最大似然估计法,我们首先要定义似然函数:

并且在

的所有取值上,使这个函数最大化(一阶导数)。这个使可能性最大的

值即被称为

的最大似然估计
离散分布,离散有限参数空间[编辑]
考虑一个抛硬币的例子。假设这个硬币正面跟反面轻重不同。我们把这个硬币抛80次(即,我们获取一个采样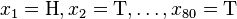
并把正面的次数记下来,正面记为H,反面记为T)。并把抛出一个正面的概率记为

,抛出一个反面的概率记为
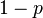
(因此,这里的

即相当于上边的

)。假设我们抛出了49个正面,31个反面,即49次H,31次T。假设这个硬币是我们从一个装了三个硬币的盒子里头取出的。这三个硬币抛出正面的概率分别为
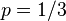
,
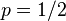
,

.这些硬币没有标记,所以我们无法知道哪个是哪个。使用最大似然估计,通过这些试验数据(即采样数据),我们可以计算出哪个硬币的可能性最大。这个似然函数取以下三个值中的一个:
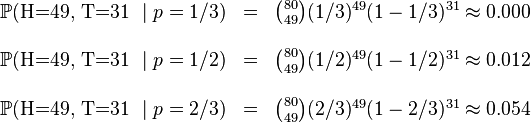
我们可以看到当

时,似然函数取得最大值。这就是

的最大似然估计。
此博客解释比较好
http://www.cnblogs.com/zhangchaoyang/articles/2623364.html
Expectation Maximization
EM是一种迭代算法,它试图找到一系列的估计参数θ(0),θ(1),θ(2),....使得训练数据的marginal likelihood是不断增加的,即:
算法刚开始的时候θ(0)赋予随机的值,每次迭代经历一个E-Step和一个M-Step,迭代终止条件是θ(i+1)与θ(i)相等或十分相近。
E-Step是在θ(i)已知的情况下计算X=x时Y=y的后验概率:

f(x|X)是一个权值,它表示观测值x在所有观察结果X中出现的频率。
M-Step:

其中

在E-Step已经求出来了。这时候可以用“令一阶导数等于0”的方法求出θ'。
EM算法收敛性的证明需要用到Jensen不等式,这里略去不讲。
Expectation Maximization
EM是一种迭代算法,它试图找到一系列的估计参数θ(0),θ(1),θ(2),....使得训练数据的marginal likelihood是不断增加的,即:
算法刚开始的时候θ(0)赋予随机的值,每次迭代经历一个E-Step和一个M-Step,迭代终止条件是θ(i+1)与θ(i)相等或十分相近。
E-Step是在θ(i)已知的情况下计算X=x时Y=y的后验概率:

f(x|X)是一个权值,它表示观测值x在所有观察结果X中出现的频率。
M-Step:

其中

在E-Step已经求出来了。这时候可以用“令一阶导数等于0”的方法求出θ'。
EM算法收敛性的证明需要用到Jensen不等式,这里略去不讲。
4最小二乘法(最小化误差的平方和 利用样本通过求导解方程组的方法求出评价函数平方和最小值进而确定模型参数)
条件:在研究两个变量之间的关系时,可以用回归分析的方法进行分析。当确定了描述两个变量之间的回归模型后,就可以使用最小二乘法估计模型中的参数,进而建立经验方程.
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
最小二乘法原理
在我们研究两个变量(x, y)之间的相互关系时,通常可以得到一系列成对的数据( x1, y1. x2, y2. … xm ,
ym );将这些数据描绘在x -y直角坐标系中,若发现这些点在一条直线附近,可以令这条直线方程如(式1-1)。
Y计= a0 + a1 X (式1-1)
其中:a0、a1 是任意实数
为建立这直线方程就要确定a0和a1,应用 最小二乘法原理 ,将实测值Yi与利用(式1-1)计算值(Y计=a0+a1X)的离差(Yi-Y计)的平方和〔∑(Yi -
Y计)2〕最小为“优化判据”。
令: φ = ∑(Yi - Y计)2 (式1-2)
把(式1-1)代入(式1-2)中得:
φ = ∑(Yi - a0 - a1 Xi)2 (式1-3)
当∑(Yi-Y计)平方最小时,可用函数 φ 对a0、a1求偏导数,令这两个偏导数等于零。

亦即:
m a0 + (∑Xi ) a1 = ∑Yi (式1-6)
(∑Xi ) a0 + (∑Xi2 ) a1 = ∑(Xi,
Yi) (式1-7)
得到的两个关于a0、 a1为未知数的两个方程组,解这两个方程组得出:
a0 = (∑Yi) / m - a1(∑Xi) / m (式1-8)
a1 = [m∑Xi Yi - (∑Xi ∑Yi)] / [m∑Xi2 -
(∑Xi)2 )] (式1-9)
这时把a0、a1代入(式1-1)中, 此时的(式1-1)就是我们回归的元线性方程即:数学模型。
在回归过程中,回归的关联式是不可能全部通过每个回归数据点( x1, y1. x2, y2. … xm ,
ym ),为了判断关联式的好坏,可借助相关系数“R”,统计量“F”,剩余标准偏差“S”进行判断;“R”越趋近于 1 越好;“F”的绝对值越大越好;“S”越趋近于 0 越好。
R = [∑XiYi - m (∑Xi / m)(∑Yi / m)]/ SQR{[∑Xi2 -
m (∑Xi / m)2][∑Yi2 - m (∑Yi / m)2]}
(式1-10) *
在(式1-1)中,m为样本容量,即实验次数;Xi、Yi分别任意一组实验X、Y的数值。
相关文章推荐
- 搜索与优化1搜索方法总结
- Deep Learning 优化方法总结
- NGUI优化方法总结
- Unity+NGUI性能优化方法总结
- Oracle数据库优化方法总结
- KERAS各种优化方法总结
- [PY3]——字符串的分割、匹配、搜索方法总结
- LBFGS优化算法以及线性搜索中zoom步长选择方法
- C++代码优化方法总结
- C++代码优化方法总结
- 组合优化问题求解方法GA-交叉算子的总结
- 各种优化方法总结比较(sgd/momentum/Nesterov/adagrad/adadelta)
- HBase性能优化方法总结
- 视图搜索排序方法总结(NotesView.FTSearchSorted)
- HBase性能优化方法总结(1):配置优化
- 优化方法(总结)
- 百度公布图文搜索结果优化方法预示着图文时代已经到来
- SEO优化之网站优化的方法总结和策略
- HBase性能优化方法总结(一):表的设计
- Spark面对OOM问题的解决方法及优化总结
