统计学习方法-Logistic（逻辑斯蒂）回归

reference： http://f.dataguru.cn/thread-128261-1-1.html http://blog.tomtung.com/2011/10/logistic-regression http://www.cnblogs.com/jerrylead/archive/2011/03/05/1971867.html http://chen.yi.bo.blog.163.com/blog/#m=0
我们在做线性回归分析时，其实是用y=mx+b直线去拟合我们的样本点，如果样本点和直线拟合很好，我们就可以得出样本点的线性相关性很强，通常用决定系数R2来表示。在寻找拟合直线的方法是最小二乘法，其实质就是找样本点离直线距离的最小平方和。这个我在白话线性回归中已经讲到。前面我都参考KHAN的统计学视频，可惜的是logistic回归里面没有讲了，今天这篇文章主要参考的是《Logistic回归模型:方法与应用》王济川，郭志刚。
为什么要用logistic回归？
我们在线性回归分析时，有时会遇到因变量y不是连续值，而是离散的，很多情况是0-1变量。如分析顾客对于商品行为的导致的结果是买（1）还是不买（0），分析股票的各种数据，因变量也是买（1）、不买（0）…。这种因变量如果我们还是使用线性回归，得到的直线一定与样本拟合得不好。举个例子，我们考察选民年收入和给某个候选人投票的相关性，如果我用线性回归来做。设回归方程为y=mx+b+e（为了严谨e为方程的干扰值，与x无关，服从正态分布，平均值为0）。显然，y=0，表示未投票；y=1表示投票。一定要记住由于e的存在，yi的值只能是一个统计值，也许每次的yi都不一样（夸张了点）。我们可以得到任意yi期望E(yi|xi)=E(mxi+b+e)=
E(mxi+b)+E(e)= E(mxi+b)+0= mxi+b。
而yi 的值取（0，1），yi期望E(yi|xi)=
P(yi=1|xi)，其实就是yi=1的条件概率（比如有5个取值0,1,1,0,1，平均值为0.6，也就是y取1的概率为0.6）。因此因变量为二分类的线性规划模型又叫线性概率模型（linear
probability model）。如果模型是线性的，很显然，如果xi是一个很大的值（如年收入1亿），那么我们得到的yi很可能大于1，相反如果年收入是一个很小的值（如-100000）,那yi的值很可能得到一个小于0的值。实际上，这很可能是个分段函数模型，这对于线性回归就不方便计算了。
什么是Logistic回归模型
但是，有一点可以确定，yi=1的概率P(yi=1|xi)与xi的应该是一个单调递增关系，用非线性模型来描述也许更加准确。这个单调关系应该是这样，xi增加时P(yi=1|xi)随之增加，到达一定的区域，这种增加时很小的，比如xi=1000000后，xi再继续增加，p的增加就不那么明显了，从统计的角度，P只能无限接近1，不能等于1。这种单调关系用S形状的曲线描述也许很合适（拟合得更好），这就是logitic函数的曲线。我们可以将事件发生的概率写成：
P(yi=1|xi)=1/（1+exp(-mx-b)） （1）
这是一个非线性函数，我们可以将其转化为一个线性函数
事件不发生的概率为P(yi=0|xi)=1-P(yi=1|xi)=1 - 1/（1+exp(-mx-b)）
事件发生概率和不发生概率之比为
p/(1-p) =exp(mx+b)两边去对数得到
ln(p/(1+p))=mx+b （2）
（1）（2）都是Logistic回归模型。
我们求解该模型，实际上就是求参数m,b。
设pi= P(yi=1|xi)是给定xi条件下y=1的概率，同样条件下得到y=0的概率为1-pi，那么，得到一个观测值（Pi=0或者1）概率为Pi=pi^yi*(1-pi)^(1-yi)。取n个观测值（n个不同xi）的分布概率为n个pi^yi*(1-pi)^(1-yi)相乘，表示为ln(θ)=Π(pi^yi*(1-pi)^(1-yi))，这就是n个观测值的似然分布函数。我们求解模型就是求解该函数最大值的参数估计值（m，b）。

————————————————————————————————————————————————————
Logistic 回归解决的并不是回归问题，而是分类问题，即目标变量（target variable）的值是离散而非连续的。这时目标变量也可称为标签（label）。如果仍用线性回归硬搞，得到的结果会非常不靠谱。

我们先考虑简单的情况：数据点只有 0 和 1 两个标签（binary classification），即[Math Processing
Error] ，且大致上是线性可分的（linearly separable）。如图：



那么现在问题就是要找到一个[Math Processing Error] ，使得直线[Math
Processing Error] 1 能够将上面图中的 positive 和 negative 两类数据点“分开”；这样的一条直线称为决策边界（decision boundary）。 ——但具体什么叫“分开”？或者说，如果已知[Math
Processing Error] ，对于一个标签未知的数据点[Math Processing
Error] ，怎么判断它是 positive 还是 negative？

直观上看，在给定[Math Processing Error] 和[Math
Processing Error] 的情况下，[Math Processing Error]
应该满足一个0-1 分布，即

[Math Processing Error]

其中[Math Processing Error] 应该满足：

首先[Math Processing Error]

若[Math Processing Error] ，我们可以认为[Math
Processing Error] 的可能性相对更大，即[Math Processing Error]
，且如果数据点离边界越远，即[Math Processing Error] 越大，[Math
Processing Error] 也应该越大。
反之，若[Math Processing Error] ，则[Math
Processing Error] ，且随[Math Processing Error]
减小而减小。
当[Math Processing Error] 时，点落在决策边界上，我们无从判断它的标签[Math
Processing Error] ，因此[Math Processing Error]
。

那[Math Processing Error] 应该取什么样的函数呢？我们知道
logistic 函数 恰巧满足上述条件，不妨就取它（“logistic 回归”也因此得名）2。即：

[Math Processing Error]

logistic 函数的图像是：



可以直观地看到它确实是满足我们要求的。这样我们就得到了：

[Math Processing Error]

我们记[Math Processing Error] ，表示这是我们希望预测的量，也就是模型的假设（hypothesis）3。在实际分类应用中，[Math
Processing Error] 时我们可以给出判断[Math Processing Error]
，[Math Processing Error] 时[Math
Processing Error] ，[Math Processing Error]
的话就蒙一个吧。

接下来[Math Processing Error] 该怎么求呢？根据log极大似然法，可知[Math
Processing Error] 的最优值就是[Math Processing Error]
，其中

[Math Processing Error]

其中第二步有点小 tricky。注意到[Math Processing Error] 在[Math
Processing Error] 时值为[Math Processing Error]
，在[Math Processing Error] 时值为[Math
Processing Error] 。这样就把[Math Processing Error]
两种取值的情况合并写在一个式子里了。

接下来我们可以求出梯度[Math Processing Error] 。如果我们像上篇笔记中一样定义：

[Math Processing Error]

可以推导得到：

[Math Processing Error]

接下来，根据梯度上升算法 4，我们就可以迭代计算下式来逼近[Math
Processing Error] ：

[Math Processing Error]

注意到这个更新式的形式和之前线性规划+最小二乘法+梯度下降得到是一样的，只是[Math Processing Error]
变了。

以上就是用梯度上升做 Logistic 回归的算法了。课上还谈到了另外 3 个问题：

如果要把 Logistic 回归推广到多个分类的情况，可以利用一种叫“1 vs all”的方法。具体地说，即每次取一个分类为 positive，其它分类都为 negative。这样针对每一个分类都学习得到一个 Logistic 回归模型。要判断一个新数据点的标签，用每一个模型都测一下，取对应[Math
Processing Error] 最大的分类为预测结果。
如果数据点不是线性可分的，类似线性回归到多项式回归（polynomial regression）的推广，可以将同一属性次数不同的项看成是彼此独立的，再和普通 Logistic 回归问题一样处理。

属性过多可能会造成模型过分复杂，导致过拟合问题。关于 overfit 和 underfit 的问题可以参见这篇文章的 3~6 段，这位学长讲得非常深入浅出了。课上提到的一种解决方法叫 regularization，即对[Math
Processing Error] 中希望加以限制的各项[Math Processing Error]
，在[Math Processing Error] 后加上[Math
Processing Error] ，使这些值过大时“惩罚”目标函数。这里[Math Processing
Error] 的取值也要注意，如果取得太小解决不了过拟合问题，但取得太大又会造成 underfit。

p.s. 今天早睡的目标又达成失败了……………………

和上节线性规划中一样，每个[Math Processing Error] 是一个[Math
Processing Error] 维向量，为书写简便我们在[Math Processing
Error] 个属性前再加一维[Math Processing Error]
。↩

这里说“不妨”似乎有点太随意了。事实上，如果假设在给定[Math Processing Error]
的情况下[Math Processing Error] 服从 0-1 分布，那么[Math
Processing Error] 取 logistic 函数实际上可以由广义线性模式（Generalized linear model）的假设推导得出。↩

注意到和上节课讲的线性回归一样，我们要预测的[Math Processing Error] 其实都是期望[Math Processing Error] 。

↩

由于这里要求的是[Math Processing Error] 的最大值，因此是梯度上升而非梯度下降。课程视频中取要最小化的目标函数[Math
Processing Error] ，因此是梯度下降。实际是一回事。↩

---------------------------------------------------------------------------------------------------------------------------------------------

1 摘要

本报告是在学习斯坦福大学机器学习课程前四节加上配套的讲义后的总结与认识。前四节主要讲述了回归问题，回归属于有监督学习中的一种方法。该方法的核心思想是从连续型统计数据中得到数学模型，然后将该数学模型用于预测或者分类。该方法处理的数据可以是多维的。

讲义最初介绍了一个基本问题，然后引出了线性回归的解决方法，然后针对误差问题做了概率解释。之后介绍了logistic回归。最后上升到理论层次，提出了一般回归。

2 问题引入

这个例子来自/article/5178345.html

假设有一个房屋销售的数据如下：

面积(m^2)	销售价钱（万元）
123	250
150	320
87	160
102	220
…	…

这个表类似于北京5环左右的房屋价钱，我们可以做出一个图，x轴是房屋的面积。y轴是房屋的售价，如下：



如果来了一个新的面积，假设在销售价钱的记录中没有的，我们怎么办呢？

我们可以用一条曲线去尽量准的拟合这些数据，然后如果有新的输入过来，我们可以在将曲线上这个点对应的值返回。如果用一条直线去拟合，可能是下面的样子：



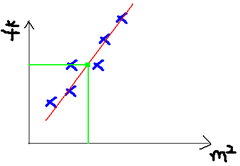
绿色的点就是我们想要预测的点。

首先给出一些概念和常用的符号。

房屋销售记录表：训练集(training set)或者训练数据(training data), 是我们流程中的输入数据，一般称为x

房屋销售价钱：输出数据，一般称为y

拟合的函数（或者称为假设或者模型）：一般写做 y = h(x)

训练数据的条目数(#training set),：一条训练数据是由一对输入数据和输出数据组成的输入数据的维度n (特征的个数，#features)

这个例子的特征是两维的，结果是一维的。然而回归方法能够解决特征多维，结果是一维多离散值或一维连续值的问题。

3 学习过程

下面是一个典型的机器学习的过程，首先给出一个输入数据，我们的算法会通过一系列的过程得到一个估计的函数，这个函数有能力对没有见过的新数据给出一个新的估计，也被称为构建一个模型。就如同上面的线性回归函数。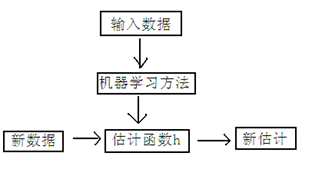

4 线性回归

线性回归假设特征和结果满足线性关系。其实线性关系的表达能力非常强大，每个特征对结果的影响强弱可以由前面的参数体现，而且每个特征变量可以首先映射到一个函数，然后再参与线性计算。这样就可以表达特征与结果之间的非线性关系。

我们用X1，X2..Xn 去描述feature里面的分量，比如x1=房间的面积，x2=房间的朝向，等等，我们可以做出一个估计函数：



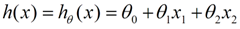
θ在这儿称为参数，在这的意思是调整feature中每个分量的影响力，就是到底是房屋的面积更重要还是房屋的地段更重要。为了如果我们令X0 = 1，就可以用向量的方式来表示了：



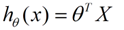
我们程序也需要一个机制去评估我们θ是否比较好，所以说需要对我们做出的h函数进行评估，一般这个函数称为损失函数（loss function）或者错误函数(error function)，描述h函数不好的程度，在下面，我们称这个函数为J函数

在这儿我们可以认为错误函数如下：



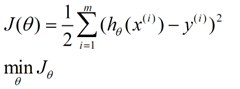
这个错误估计函数是去对x(i)的估计值与真实值y(i)差的平方和作为错误估计函数，前面乘上的1/2是为了在求导的时候，这个系数就不见了。

至于为何选择平方和作为错误估计函数，讲义后面从概率分布的角度讲解了该公式的来源。

如何调整θ以使得J(θ)取得最小值有很多方法，其中有最小二乘法(min square)，是一种完全是数学描述的方法，和梯度下降法。

5 梯度下降法

在选定线性回归模型后，只需要确定参数θ，就可以将模型用来预测。然而θ需要在J(θ)最小的情况下才能确定。因此问题归结为求极小值问题，使用梯度下降法。梯度下降法最大的问题是求得有可能是全局极小值，这与初始点的选取有关。

梯度下降法是按下面的流程进行的：

1）首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。

2）改变θ的值，使得J(θ)按梯度下降的方向进行减少。

梯度方向由J(θ)对θ的偏导数确定，由于求的是极小值，因此梯度方向是偏导数的反方向。结果为



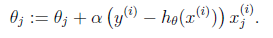
迭代更新的方式有两种，一种是批梯度下降，也就是对全部的训练数据求得误差后再对θ进行更新，另外一种是增量梯度下降，每扫描一步都要对θ进行更新。前一种方法能够不断收敛，后一种方法结果可能不断在收敛处徘徊。

一般来说，梯度下降法收敛速度还是比较慢的。

另一种直接计算结果的方法是最小二乘法。

6 最小二乘法

将训练特征表示为X矩阵，结果表示成y向量，仍然是线性回归模型，误差函数不变。那么θ可以直接由下面公式得出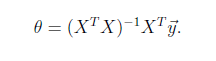





但此方法要求X是列满秩的，而且求矩阵的逆比较慢。

7 选用误差函数为平方和的概率解释

假设根据特征的预测结果与实际结果有误差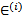

，那么预测结果

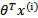
和真实结果

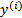
满足下式：





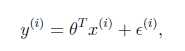
一般来讲，误差满足平均值为0的高斯分布，也就是正态分布。那么x和y的条件概率也就是





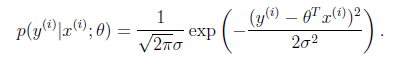
这样就估计了一条样本的结果概率，然而我们期待的是模型能够在全部样本上预测最准，也就是概率积最大。注意这里的概率积是概率密度函数积，连续函数的概率密度函数与离散值的概率函数不同。这个概率积成为最大似然估计。我们希望在最大似然估计得到最大值时确定θ。那么需要对最大似然估计公式求导，求导结果既是



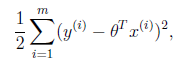
这就解释了为何误差函数要使用平方和。

当然推导过程中也做了一些假定，但这个假定符合客观规律。

8 带权重的线性回归

上面提到的线性回归的误差函数里系统都是1，没有权重。带权重的线性回归加入了权重信息。

基本假设是



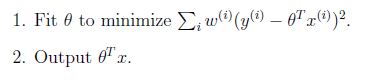
其中假设

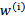
符合公式



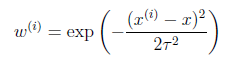
其中x是要预测的特征，这样假设的道理是离x越近的样本权重越大，越远的影响越小。这个公式与高斯分布类似，但不一样，因为

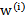
不是随机变量。

此方法成为非参数学习算法，因为误差函数随着预测值的不同而不同，这样θ无法事先确定，预测一次需要临时计算，感觉类似KNN。

9 分类和logistic回归

一般来说，回归不用在分类问题上，因为回归是连续型模型，而且受噪声影响比较大。如果非要应用进入，可以使用logistic回归。

logistic回归本质上是线性回归，只是在特征到结果的映射中加入了一层函数映射，即先把特征线性求和，然后使用函数g(z)将最为假设函数来预测。g(z)可以将连续值映射到0和1上。

logistic回归的假设函数如下，线性回归假设函数只是

。





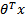
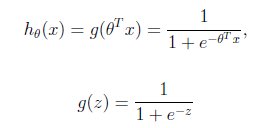
logistic回归用来分类0/1问题，也就是预测结果属于0或者1的二值分类问题。这里假设了二值满足伯努利分布，也就是





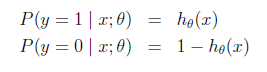
当然假设它满足泊松分布、指数分布等等也可以，只是比较复杂，后面会提到线性回归的一般形式。

与第7节一样，仍然求的是最大似然估计，然后求导，得到迭代公式结果为



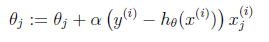
可以看到与线性回归类似，只是

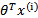
换成了

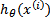
，而

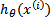
实际上就是

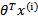
经过g(z)映射过来的。

10 牛顿法来解最大似然估计

第7和第9节使用的解最大似然估计的方法都是求导迭代的方法，这里介绍了牛顿下降法，使结果能够快速的收敛。

当要求解

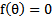
时，如果f可导，那么可以通过迭代公式





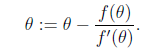
来迭代求解最小值。

当应用于求解最大似然估计的最大值时，变成求解最大似然估计概率导数

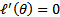
的问题。

那么迭代公式写作



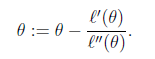
当θ是向量时，牛顿法可以使用下面式子表示



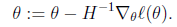
其中

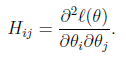
是n×n的Hessian矩阵。

牛顿法收敛速度虽然很快，但求Hessian矩阵的逆的时候比较耗费时间。

当初始点X0靠近极小值X时，牛顿法的收敛速度是最快的。但是当X0远离极小值时，牛顿法可能不收敛，甚至连下降都保证不了。原因是迭代点Xk+1不一定是目标函数f在牛顿方向上的极小点。

11 一般线性模型

之所以在logistic回归时使用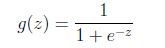



的公式是由一套理论作支持的。

这个理论便是一般线性模型。

首先，如果一个概率分布可以表示成



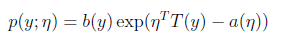
时，那么这个概率分布可以称作是指数分布。

伯努利分布，高斯分布，泊松分布，贝塔分布，狄特里特分布都属于指数分布。

在logistic回归时采用的是伯努利分布，伯努利分布的概率可以表示成



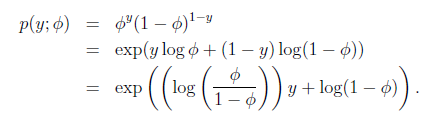
其中



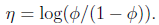
得到



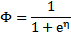
这就解释了logistic回归时为了要用这个函数。

一般线性模型的要点是

1）



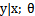
满足一个以

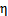
为参数的指数分布，那么可以求得

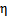
的表达式。

2） 给定x，我们的目标是要确定

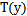
，大多数情况下

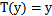
，那么我们实际上要确定的是

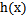
，而

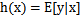
。（在logistic回归中期望值是

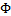
，因此h是

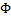
；在线性回归中期望值是

，而高斯分布中

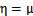
，因此线性回归中h=

）。

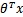
3）

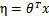
12 Softmax回归

最后举了一个利用一般线性模型的例子。

假设预测值y有k种可能，即y∈{1,2,…,k}

比如k=3时，可以看作是要将一封未知邮件分为垃圾邮件、个人邮件还是工作邮件这三类。

定义



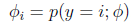
那么



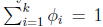
这样



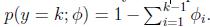
即式子左边可以有其他的概率表示，因此可以当作是k-1维的问题。

为了表示多项式分布表述成指数分布，我们引入T(y)，它是一组k-1维的向量，这里的T(y)不是y，T(y)i表示T(y)的第i个分量。



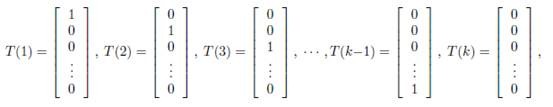
应用于一般线性模型，结果y必然是k中的一种。1{y=k}表示当y=k的时候，1{y=k}=1。那么p(y)可以表示为



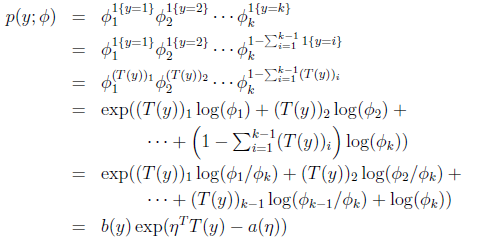
其实很好理解，就是当y是一个值m（m从1到k）的时候，p(y)=

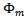
，然后形式化了一下。

那么



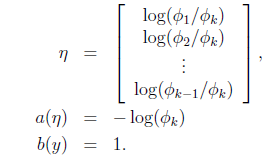
最后求得



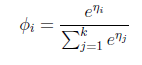
而y=i时



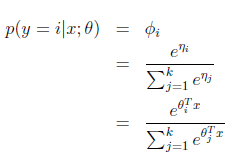
求得期望值





那么就建立了假设函数，最后就获得了最大似然估计





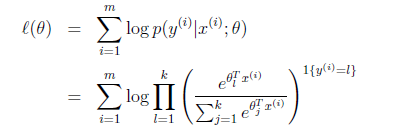
对该公式可以使用梯度下降或者牛顿法迭代求解。

解决了多值模型建立与预测问题。

学习总结

该讲义组织结构清晰，思路独特，讲原因，也讲推导。可贵的是讲出了问题的基本解决思路和扩展思路，更重要的是讲出了为什么要使用相关方法以及问题根源。在看似具体的解题思路中能引出更为抽象的一般解题思路，理论化水平很高。

该方法可以用在对数据多维分析和多值预测上，更适用于数据背后蕴含某种概率模型的情景。

几个问题

一是采用迭代法的时候，步长怎么确定比较好

而是最小二乘法的矩阵形式是否一般都可用

——————————————————————————————————————————————————————————————————————————

前面写了一些读书笔记是关于用logit回归做二分类问题后的效果评价，基本上已经可以告一段落。然后打算回过头来整理一下logit回归本身的一些思路。很惭愧，我不是统计学出身，当年概率论差点考挂，数理统计也是一门选修课（唯一印象深刻的是老师的口音），所以大概很难从理论上进行严格的阐述，主要还是写一点直观的理解。

限制一下问题的范围吧，基本上用到logistic回归的，很多是二分类问题，也就是因变量是0-1类型的情况。我们想要研究的是因变量与自变量之间的关系，跟线性回归是完全类似的问题。但是由于因变量形式比较特殊，所以造成了处理方式的不同，也就引出了我的第一个困惑：为什么要引进广义回归方法呢？

首先，假设我们从线性回归的思路出发，遇到的第一个问题就是，我们问题的因变量是什么？这个因变量是一个分类的变量，看一下散点图就能知道因变量与自变量之间不是那种直线的关系，这就导致我们没办法写出传统的那种比较容易理解的线性回归公式 y = a + b*x 。我们想到的一个解决办法是，将这个因变量抽象成它的期望值（这应该是广义线性回归的核心内容之一）。在0-1变量的情形下，这个期望值就等于因变量取1的概率，一般就写成P了。这个P貌似是可以涵盖了0-1因变量的信息，同时也能够用来比较直观地理解我们的问题：当自变量发生变化时，我们的目标变量取1的概率是怎样变化的。

然后，我们继续试图用线性回归的思路，把问题写成 P = a + b*x ，也就是说，我们假设因变量取1的概率跟自变量是线性关系。这个假设挺自然也挺合理的，但是却导致了另外三个问题：参数估计，因变量P的取值范围，以及非正态的误差。由于这里的P是我们抽象出来的一个变量，我们没办法从观测数据中得到这个值，所以也就没办法用我们熟悉的最小二乘法，而如果不用最小二乘法，说实话，我还真不知道应该用什么方法来估计参数（知识太有限了）。另一方面，等式右边是自变量x的线性函数，于是他的取值范围是负无穷到正无穷，这显然与等式左边的概率P的取值范围相矛盾，是不合理的。同时，非正态的误差也与线性回归的基本假设相违背。

于是，我们就得想办法对上面的这个回归公式 P = a + b*x 做一些调整，这里就涉及到了广义线性回归的另一个核心内容，连接函数。连接函数可以认为是对等式左边的概率P做一点变换，使得我们能够有办法进行参数估计，并且让变化之后的取值范围变得合理。参数估计这块，我不是非常明白，因为可能涉及分布族的一些理论，貌似是为了能够方便地进行极大似然估计。而对取值范围进行缩放变换似乎稍微容易理解一点，就是努力地将P的[0,1]限制取消。这里常用的连接函数就是logit()与probit()。经过变换后，回归公式变成了：
logit(P) = log(P / (1-P)) = a + b*x 以及 probit(P) = a + b*x
这两个连接函数的性质使得P的取值被放大到整个实数轴上。
事实上可以把上面的公式改写一下：
P = exp(a + b*x) / (1 + exp(a + b*x)) 或者 P = pnorm(a + b*x)（这个是标准正态分布的分布函数）
可以看出，公式右边的取值被限制到[0,1]上了，从而使得公式变得合理。
但是，能够实现这种[0,1]限制的函数应该也蛮多的，为啥会推荐这两个变换呢？这个应该跟业务理解有关。
可以先看一下经过变换后，自变量和P的关系是个什么样子。





上半部分图形显示了概率P随着自变量变化而变化的情况，下半部分图形显示了这种变化的速度的变化（没记错的话，分布函数求导应该就是密度函数）。可以看得出来，概率P与自变量仍然存在或多或少的线性关系，主要是在头尾两端被连接函数扭曲了，从而实现了[0,1]限制。同时，自变量取值靠近中间的时候，概率P变化比较快，自变量取值靠近两端的时候，概率P基本不再变化。这就跟我们的直观理解相符合了，似乎是某种边际效用递减的特点，不恰当的例子就是我们青春期的时候狂长个子而当青春期过去我们的个头就基本稳定了。（确实是个不恰当的例子，恰当的例子暂时没想到。）这就基本解释了我们选择这两个变化作为连接函数的一部分原因。

同时也可以看出来，logit跟probit的形式虽然不同，外观还是蛮相似的。前几天我还跟老段讨论这个来着，我当时以为probit回归是跟logit回归完全不同的假设，看来是理解不够的缘故。

顺便来画一下不同系数的效果。





到这里，logit回归就基本成型了，里面用到比较重要的内容是”求期望“和”连接函数“，最后的回归公式就是



有这个形式，就比较容易用似然函数的方法进行参数估计了。

先到这里，打完收工。