2013年ACM网络赛杭州赛区
2013-09-16 08:27
369 查看
点击打开链接
Total Submission(s): 446 Accepted Submission(s): 193
[align=left]Problem Description[/align]
Caocao was defeated by Zhuge Liang and Zhou Yu in the battle of Chibi. But he wouldn't give up. Caocao's army still was not good at water battles, so he came up with another idea. He built many islands in the Changjiang river, and
based on those islands, Caocao's army could easily attack Zhou Yu's troop. Caocao also built bridges connecting islands. If all islands were connected by bridges, Caocao's army could be deployed very conveniently among those islands. Zhou Yu couldn't stand
with that, so he wanted to destroy some Caocao's bridges so one or more islands would be seperated from other islands. But Zhou Yu had only one bomb which was left by Zhuge Liang, so he could only destroy one bridge. Zhou Yu must send someone carrying the
bomb to destroy the bridge. There might be guards on bridges. The soldier number of the bombing team couldn't be less than the guard number of a bridge, or the mission would fail. Please figure out as least how many soldiers Zhou Yu have to sent to complete
the island seperating mission.
[align=left]Input[/align]
There are no more than 12 test cases.
In each test case:
The first line contains two integers, N and M, meaning that there are N islands and M bridges. All the islands are numbered from 1 to N. ( 2 <= N <= 1000, 0 < M <= N2 )
Next M lines describes M bridges. Each line contains three integers U,V and W, meaning that there is a bridge connecting island U and island V, and there are W guards on that bridge. ( U ≠ V and 0 <= W <= 10,000 )
The input ends with N = 0 and M = 0.
[align=left]Output[/align]
For each test case, print the minimum soldier number Zhou Yu had to send to complete the mission. If Zhou Yu couldn't succeed any way, print -1 instead.
[align=left]Sample Input[/align]
3 3
1 2 7
2 3 4
3 1 4
3 2
1 2 7
2 3 4
0 0
[align=left]Sample Output[/align]
-1
4
[align=left]Source[/align]
2013 ACM/ICPC Asia Regional Hangzhou Online
[align=left]Recommend[/align]
liuyiding
题意是说曹操有n个岛,岛与岛之间有桥,桥上有士兵看守。周瑜想要派兵去炸掉桥,但是只能炸一次,而且兵数必须不少于看守桥的士兵。问你周瑜最少派多少兵,就可以将曹操的一个岛或者一些岛跟其它的岛相离。如果周瑜不能成功,则输出-1.
此题是双联通分量求割桥的类型。另外此题有不少坑:
1:可能有重边。
2:如果最小边权为0,则需要一个人。
3:如果原图不连通,则输出0.
点击打开链接
Total Submission(s): 309 Accepted Submission(s): 119
[align=left]Problem Description[/align]
There was no donkey in the province of Gui Zhou, China. A trouble maker shipped one and put it in the forest which could be considered as an N×N grid. The coordinates of the up-left cell is (0,0) , the down-right cell is (N-1,N-1)
and the cell below the up-left cell is (1,0)..... A 4×4 grid is shown below:
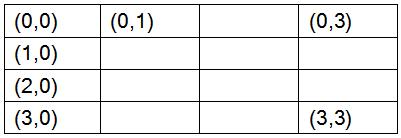
The donkey lived happily until it saw a tiger far away. The donkey had never seen a tiger ,and the tiger had never seen a donkey. Both of them were frightened and wanted to escape from each other. So they started running fast. Because they were scared, they
were running in a way that didn't make any sense. Each step they moved to the next cell in their running direction, but they couldn't get out of the forest. And because they both wanted to go to new places, the donkey would never stepped into a cell which
had already been visited by itself, and the tiger acted the same way. Both the donkey and the tiger ran in a random direction at the beginning and they always had the same speed. They would not change their directions until they couldn't run straight ahead
any more. If they couldn't go ahead any more ,they changed their directions immediately. When changing direction, the donkey always turned right and the tiger always turned left. If they made a turn and still couldn't go ahead, they would stop running and
stayed where they were, without trying to make another turn. Now given their starting positions and directions, please count whether they would meet in a cell.
[align=left]Input[/align]
There are several test cases.
In each test case:
First line is an integer N, meaning that the forest is a N×N grid.
The second line contains three integers R, C and D, meaning that the donkey is in the cell (R,C) when they started running, and it's original direction is D. D can be 0, 1, 2 or 3. 0 means east, 1 means south , 2 means west, and 3 means north.
The third line has the same format and meaning as the second line, but it is for the tiger.
The input ends with N = 0. ( 2 <= N <= 1000, 0 <= R, C < N)
[align=left]Output[/align]
For each test case, if the donkey and the tiger would meet in a cell, print the coordinate of the cell where they meet first time. If they would never meet, print -1 instead.
[align=left]Sample Input[/align]
2
0 0 0
0 1 2
4
0 1 0
3 2 0
0
[align=left]Sample Output[/align]
-1
1 3
[align=left]Source[/align]
2013 ACM/ICPC Asia Regional Hangzhou Online
[align=left]Recommend[/align]
liuyiding
比赛时间花了三个小时硬是没做出来了,明明都想到是搜索和模拟了,哎,比赛完之后又做了两个小时才做出来,害的我都失眠了,网络赛真是伤不起。
题意是说在一个n*n的矩阵里面,有一只驴和一只老虎,给了你它们的起始坐标和方向,当它们无路可走的时候,驴总是向右拐,如果仍然走不动,则停止;而老虎总是向左拐,如果仍然走不动的话,也停止。如果它们在途中相遇,输出相遇时的坐标,如果始终相遇不到,则输出-1.
Caocao's Bridges
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 446 Accepted Submission(s): 193
[align=left]Problem Description[/align]
Caocao was defeated by Zhuge Liang and Zhou Yu in the battle of Chibi. But he wouldn't give up. Caocao's army still was not good at water battles, so he came up with another idea. He built many islands in the Changjiang river, and
based on those islands, Caocao's army could easily attack Zhou Yu's troop. Caocao also built bridges connecting islands. If all islands were connected by bridges, Caocao's army could be deployed very conveniently among those islands. Zhou Yu couldn't stand
with that, so he wanted to destroy some Caocao's bridges so one or more islands would be seperated from other islands. But Zhou Yu had only one bomb which was left by Zhuge Liang, so he could only destroy one bridge. Zhou Yu must send someone carrying the
bomb to destroy the bridge. There might be guards on bridges. The soldier number of the bombing team couldn't be less than the guard number of a bridge, or the mission would fail. Please figure out as least how many soldiers Zhou Yu have to sent to complete
the island seperating mission.
[align=left]Input[/align]
There are no more than 12 test cases.
In each test case:
The first line contains two integers, N and M, meaning that there are N islands and M bridges. All the islands are numbered from 1 to N. ( 2 <= N <= 1000, 0 < M <= N2 )
Next M lines describes M bridges. Each line contains three integers U,V and W, meaning that there is a bridge connecting island U and island V, and there are W guards on that bridge. ( U ≠ V and 0 <= W <= 10,000 )
The input ends with N = 0 and M = 0.
[align=left]Output[/align]
For each test case, print the minimum soldier number Zhou Yu had to send to complete the mission. If Zhou Yu couldn't succeed any way, print -1 instead.
[align=left]Sample Input[/align]
3 3
1 2 7
2 3 4
3 1 4
3 2
1 2 7
2 3 4
0 0
[align=left]Sample Output[/align]
-1
4
[align=left]Source[/align]
2013 ACM/ICPC Asia Regional Hangzhou Online
[align=left]Recommend[/align]
liuyiding
题意是说曹操有n个岛,岛与岛之间有桥,桥上有士兵看守。周瑜想要派兵去炸掉桥,但是只能炸一次,而且兵数必须不少于看守桥的士兵。问你周瑜最少派多少兵,就可以将曹操的一个岛或者一些岛跟其它的岛相离。如果周瑜不能成功,则输出-1.
此题是双联通分量求割桥的类型。另外此题有不少坑:
1:可能有重边。
2:如果最小边权为0,则需要一个人。
3:如果原图不连通,则输出0.
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define M 10010
#define inf 0x3f3f3f3f
using namespace std;
int dfn[M],low[M],head[M],pre[M];
int n,m,tot,ind;
struct Edg
{
int to,next,w;
bool cut;
}edg[2000010];
void init()
{
tot=0;
ind=0;
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
memset(head,-1,sizeof(head));
for(int i=0;i<=n;i++)
pre[i]=i;
}
void addedge(int u,int v,int w)
{
edg[tot].to=v;edg[tot].next=head[u];
edg[tot].w=w;edg[tot].cut=false;//初始化
head[u]=tot++;
}
int find(int x)
{
while(x!=pre[x])
x=pre[x];
return x;
}
void unio(int a,int b)
{
int x=find(a);
int y=find(b);
if(x!=y)
pre[x]=y;
}
int dfs(int u,int pre)
{
dfn[u]=low[u]=++ind;
int sum=0,v;
for(int i=head[u];i!=-1;i=edg[i].next)
{
v=edg[i].to;
if(v==pre&&sum==0)
{
sum++;
continue;
}
if(!dfn[v])
{
dfs(v,u);
if(low[u]>low[v])
low[u]=low[v];
if(low[v]>dfn[u])//一条无向边(u,v)是桥,当且仅当(u,v)为树枝边,且满足DFS(u)<Low(v)
{
edg[i].cut=true;
edg[i^1].cut=true;
}
}
else if(low[u]>dfn[v])
low[u]=dfn[v];
}
}
int tarjan(int n)
{
for(int i=1;i<=n;i++)
if(!dfn[i])
dfs(i,i);
int answer=inf;
for(int u=1;u<=n;u++)
for(int i=head[u];i!=-1;i=edg[i].next)
if(edg[i].cut)
answer=min(answer,edg[i].w);//找最小的桥
if(answer==inf)return -1;
if(answer==0)answer++;//如果割的桥为0,则要+1
return answer;
}
int main()
{
//freopen("in.txt","r",stdin);
while(scanf("%d%d",&n,&m),n|m)
{
init();
int a,b,c;
while(m--)
{
scanf("%d%d%d",&a,&b,&c);
if(a==b)continue;
addedge(a,b,c);
addedge(b,a,c);
unio(a,b);
}
bool flag=true;
for(int i=1;i<=n;i++)//判断是否联通
if(find(i)!=find(1))
flag=false;
if(!flag)
printf("0\n");
else
printf("%d\n",tarjan(n));
}
return 0;
}点击打开链接
The Donkey of Gui Zhou
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 309 Accepted Submission(s): 119
[align=left]Problem Description[/align]
There was no donkey in the province of Gui Zhou, China. A trouble maker shipped one and put it in the forest which could be considered as an N×N grid. The coordinates of the up-left cell is (0,0) , the down-right cell is (N-1,N-1)
and the cell below the up-left cell is (1,0)..... A 4×4 grid is shown below:

The donkey lived happily until it saw a tiger far away. The donkey had never seen a tiger ,and the tiger had never seen a donkey. Both of them were frightened and wanted to escape from each other. So they started running fast. Because they were scared, they
were running in a way that didn't make any sense. Each step they moved to the next cell in their running direction, but they couldn't get out of the forest. And because they both wanted to go to new places, the donkey would never stepped into a cell which
had already been visited by itself, and the tiger acted the same way. Both the donkey and the tiger ran in a random direction at the beginning and they always had the same speed. They would not change their directions until they couldn't run straight ahead
any more. If they couldn't go ahead any more ,they changed their directions immediately. When changing direction, the donkey always turned right and the tiger always turned left. If they made a turn and still couldn't go ahead, they would stop running and
stayed where they were, without trying to make another turn. Now given their starting positions and directions, please count whether they would meet in a cell.
[align=left]Input[/align]
There are several test cases.
In each test case:
First line is an integer N, meaning that the forest is a N×N grid.
The second line contains three integers R, C and D, meaning that the donkey is in the cell (R,C) when they started running, and it's original direction is D. D can be 0, 1, 2 or 3. 0 means east, 1 means south , 2 means west, and 3 means north.
The third line has the same format and meaning as the second line, but it is for the tiger.
The input ends with N = 0. ( 2 <= N <= 1000, 0 <= R, C < N)
[align=left]Output[/align]
For each test case, if the donkey and the tiger would meet in a cell, print the coordinate of the cell where they meet first time. If they would never meet, print -1 instead.
[align=left]Sample Input[/align]
2
0 0 0
0 1 2
4
0 1 0
3 2 0
0
[align=left]Sample Output[/align]
-1
1 3
[align=left]Source[/align]
2013 ACM/ICPC Asia Regional Hangzhou Online
[align=left]Recommend[/align]
liuyiding
比赛时间花了三个小时硬是没做出来了,明明都想到是搜索和模拟了,哎,比赛完之后又做了两个小时才做出来,害的我都失眠了,网络赛真是伤不起。
题意是说在一个n*n的矩阵里面,有一只驴和一只老虎,给了你它们的起始坐标和方向,当它们无路可走的时候,驴总是向右拐,如果仍然走不动,则停止;而老虎总是向左拐,如果仍然走不动的话,也停止。如果它们在途中相遇,输出相遇时的坐标,如果始终相遇不到,则输出-1.
#include<stdio.h>
#include<string.h>
#define M 1007
using namespace std;
int vis1[M][M],vis2[M][M];
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
int n,x1,y1,d1,x2,y2,d2;
int main()
{
while(scanf("%d",&n),n)
{
scanf("%d%d%d",&x1,&y1,&d1);
scanf("%d%d%d",&x2,&y2,&d2);
memset(vis1,0,sizeof(vis1));
memset(vis2,0,sizeof(vis2));
bool flag=false,stop1=false,stop2=false;
vis1[x1][y1]=1;
vis2[x2][y2]=1;
int xx1,yy1,xx2,yy2;
while(1)
{
if(x1==x2&&y1==y2)
{
flag=true;
break;
}
if(stop1&&stop2)//如果两个都停下来了,则结束,它们不能相遇
break;
vis1[x1][y1]=1;
vis2[x2][y2]=1;
if(!stop1)//如果驴还没有停下来
{
xx1=x1+dx[d1];
yy1=y1+dy[d1];
if(xx1>=0&&xx1<n&&yy1>=0&&yy1<n&&!vis1[xx1][yy1])//如果能够继续往前走
{
x1=xx1;
y1=yy1;
d1=d1;
}
else//不能继续走了
{
xx1=x1+dx[(d1+1)%4];//转了方向之后的坐标
yy1=y1+dy[(d1+1)%4];
if(xx1>=0&&xx1<n&&yy1>=0&&yy1<n&&!vis1[xx1][yy1])//如果转了方向之后能够继续走
{
x1=xx1;
y1=yy1;
d1=(d1+1)%4;
}
else//如果转了方向之后不能走了
{
x1=x1;
y1=y1;
stop1=true;//就停下来
}
}
}
if(!stop2)//同驴一样
{
xx2=x2+dx[d2];
yy2=y2+dy[d2];
if(xx2>=0&&xx2<n&&yy2>=0&&yy2<n&&!vis2[xx2][yy2])
{
x2=xx2;
y2=yy2;
d2=d2;
}
else
{
xx2=x2+dx[((d2-1)%4+4)%4];
yy2=y2+dy[((d2-1)%4+4)%4];
if(xx2>=0&&xx2<n&&yy2>=0&&yy2<n&&!vis2[xx2][yy2])
{
x2=xx2;
y2=yy2;
d2=((d2-1)%4+4)%4;
}
else
{
x2=x2;
y2=y2;
stop2=true;
}
}
}
}
if(flag)
printf("%d %d\n",x1,y1);
else
printf("-1\n");
}
return 0;
}相关文章推荐
- HDU4577(2013年ACM杭州赛区邀请赛B题)
- hdu 4741 Save Labman No.004 [2013年杭州ACM网络赛]
- hdu 4738 Caocao's Bridges 2013 ACM-ICPC杭州赛区网络赛 1001 双连通分量
- HDU 4419 Colourful Rectangle 第37届ACM/ICPC 杭州赛区网络赛 1010题 (线段树)
- HDU4414 2012ACM/ICPC杭州赛区网络赛E Finding crosses
- 2013年杭州赛区网络赛The Donkey of Gui Zhou
- HDU4415 Assassin’s Creed 2012ACM/ICPC 杭州赛区网络赛 F
- HDU 4417 Super Mario 第37届ACM/ICPC 杭州赛区网络赛1008题(树状数组或者线段树)
- 2012 ACM/ICPC 杭州赛区网络赛Super Mario
- 2013年ACM网络赛长春赛区
- hdu 4741 Save Labman No.004 [2013年杭州ACM网络赛]
- HDU 4417 Super Mario 第37届ACM/ICPC 杭州赛区网络赛第1008题 (划分树)
- HDU4415 Assassin’s Creed 2012ACM/ICPC 杭州赛区网络赛 F
- 2013年ACM网络赛成都赛区
- 2017 ACM-ICPC 亚洲区(西安赛区)网络赛 E Maximum Flow
- 计蒜客 16950 Banana(2017 ACM-ICPC 亚洲区(乌鲁木齐赛区)网络赛 A)
- HDU 4278 Faulty Odometer 第37届ACM/ICPC天津赛区网络赛1001题 (简单水题)
- ACM-ICPC国际大学生程序设计竞赛北京赛区(2017)网络赛 I.Minimum(线段树区间极值+分类讨论)
- 2017 ACM-ICPC 亚洲区(南宁赛区)网络赛 B.Train Seats Reservation(模拟)
- 2017 ACM-ICPC 亚洲区(南宁赛区)网络赛 - B F J L M
