混合高斯模型(应用和EM算法)
2011-12-20 16:51
211 查看
这篇讨论使用期望最大化算法(Expectation-Maximization)来进行密度估计(density estimation)。
与k-means一样,给定的训练样本是
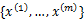
,我们将隐含类别标签用
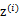
表示。与k-means的硬指定不同,我们首先认为
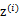
是满足一定的概率分布的,这里我们认为满足多项式分布,
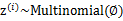
,其中
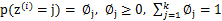
,
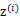
有k个值{1,…,k}可以选取。而且我们认为在给定
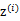
后,
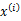
满足多值高斯分布,即
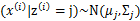
。由此可以得到联合分布
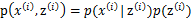
。
整个模型简单描述为对于每个样例
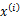
,我们先从k个类别中按多项式分布抽取一个
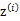
,然后根据
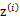
所对应的k个多值高斯分布中的一个生成样例
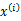
,。整个过程称作混合高斯模型。注意的是这里的
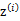
仍然是隐含随机变量。模型中还有三个变量
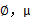
和
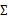
。最大似然估计为
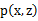
。对数化后如下:
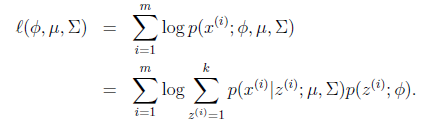
这个式子的最大值是不能通过前面使用的求导数为0的方法解决的,因为求的结果不是close form。但是假设我们知道了每个样例的
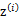
,那么上式可以简化为:
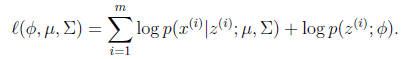
这时候我们再来对
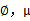
和
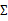
进行求导得到:
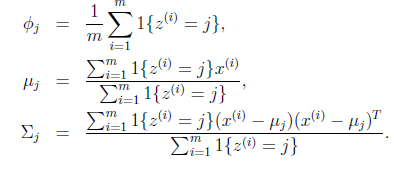

就是样本类别中
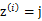
的比率。
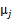
是类别为j的样本特征均值,
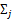
是类别为j的样例的特征的协方差矩阵。
实际上,当知道
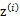
后,最大似然估计就近似于高斯判别分析模型(Gaussian
discriminant analysis model)了。所不同的是GDA中类别y是伯努利分布,而这里的z是多项式分布,还有这里的每个样例都有不同的协方差矩阵,而GDA中认为只有一个。
之前我们是假设给定了
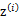
,实际上
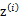
是不知道的。那么怎么办呢?考虑之前提到的EM的思想,第一步是猜测隐含类别变量z,第二步是更新其他参数,以获得最大的最大似然估计。用到这里就是:
在E步中,我们将其他参数
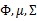
看作常量,计算
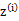
的后验概率,也就是估计隐含类别变量。估计好后,利用上面的公式重新计算其他参数,计算好后发现最大化最大似然估计时,
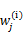
值又不对了,需要重新计算,周而复始,直至收敛。
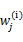
的具体计算公式如下:
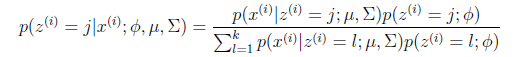
这个式子利用了贝叶斯公式。
这里我们使用
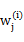
代替了前面的
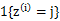
,由简单的0/1值变成了概率值。
对比K-means可以发现,这里使用了“软”指定,为每个样例分配的类别
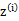
是有一定的概率的,同时计算量也变大了,每个样例i都要计算属于每一个类别j的概率。与K-means相同的是,结果仍然是局部最优解。对其他参数取不同的初始值进行多次计算不失为一种好方法。
文章转载自:/article/5718123.html
与k-means一样,给定的训练样本是
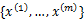
,我们将隐含类别标签用
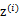
表示。与k-means的硬指定不同,我们首先认为
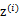
是满足一定的概率分布的,这里我们认为满足多项式分布,
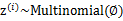
,其中
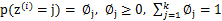
,
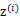
有k个值{1,…,k}可以选取。而且我们认为在给定
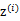
后,
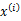
满足多值高斯分布,即
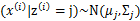
。由此可以得到联合分布
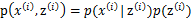
。
整个模型简单描述为对于每个样例
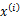
,我们先从k个类别中按多项式分布抽取一个
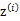
,然后根据
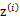
所对应的k个多值高斯分布中的一个生成样例
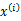
,。整个过程称作混合高斯模型。注意的是这里的
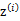
仍然是隐含随机变量。模型中还有三个变量
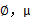
和
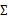
。最大似然估计为
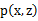
。对数化后如下:
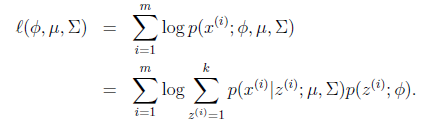
这个式子的最大值是不能通过前面使用的求导数为0的方法解决的,因为求的结果不是close form。但是假设我们知道了每个样例的
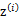
,那么上式可以简化为:
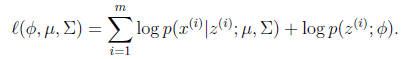
这时候我们再来对
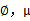
和
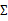
进行求导得到:
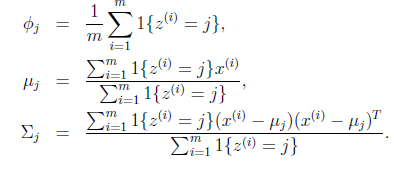

就是样本类别中
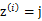
的比率。
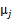
是类别为j的样本特征均值,
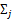
是类别为j的样例的特征的协方差矩阵。
实际上,当知道
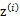
后,最大似然估计就近似于高斯判别分析模型(Gaussian
discriminant analysis model)了。所不同的是GDA中类别y是伯努利分布,而这里的z是多项式分布,还有这里的每个样例都有不同的协方差矩阵,而GDA中认为只有一个。
之前我们是假设给定了
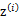
,实际上
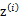
是不知道的。那么怎么办呢?考虑之前提到的EM的思想,第一步是猜测隐含类别变量z,第二步是更新其他参数,以获得最大的最大似然估计。用到这里就是:
| 循环下面步骤,直到收敛: { (E步)对于每一个i和j,计算 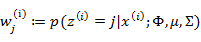 (M步),更新参数: 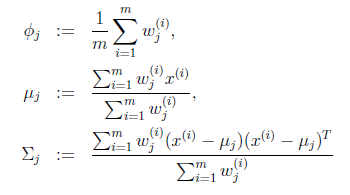 } |
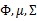
看作常量,计算
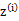
的后验概率,也就是估计隐含类别变量。估计好后,利用上面的公式重新计算其他参数,计算好后发现最大化最大似然估计时,
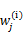
值又不对了,需要重新计算,周而复始,直至收敛。
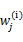
的具体计算公式如下:
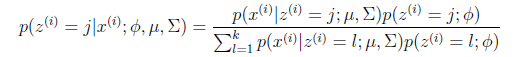
这个式子利用了贝叶斯公式。
这里我们使用
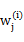
代替了前面的
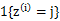
,由简单的0/1值变成了概率值。
对比K-means可以发现,这里使用了“软”指定,为每个样例分配的类别
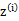
是有一定的概率的,同时计算量也变大了,每个样例i都要计算属于每一个类别j的概率。与K-means相同的是,结果仍然是局部最优解。对其他参数取不同的初始值进行多次计算不失为一种好方法。
文章转载自:/article/5718123.html
相关文章推荐
- EM算法应用到 因子分析
- EM算法的理解以及应用
- CS229课程笔记12:EM算法及混合高斯的应用
- 【机器学习笔记】EM算法及其应用
- EM算法 估计混合高斯模型参数 Python实现
- 混合高斯模型(Mixtures of Gaussians)和EM算法
- EM算法--应用到三个模型: 高斯混合模型 ,混合朴素贝叶斯模型,因子分析模型
- 机器学习:混合高斯模型和EM算法
- GMM混合高斯模型理论基础(基于EM算法)
- 机器学习3_EM算法与混合高斯模型
- 混合高斯模型(Mixtures of Gaussians)和EM算法
- EM算法的应用--高斯混合模型学习
- EM算法与在高斯混合模型中的应用
- 【机器学习-斯坦福】学习笔记11 混合高斯模型(Mixtures of Gaussians)和EM算法
- GMM混合高斯模型的EM算法及Python实现
- EM算法 - 2 - EM算法在高斯混合模型学习中的应用
- 混合高斯模型(Mixtures of Gaussians)和EM算法
- EM算法结合GMM混合高斯模型
- 混合高斯模型(Mixtures of Gaussians)和EM算法
- 聚类与EM算法——混合高斯模型
