论文解读(Cluster-GCN)《Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks》
论文信息
论文标题:Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks
论文作者:Wei-Lin Chiang, Xuanqing Liu, Si Si, Yang Li, Samy Bengio, Cho-Jui Hsieh
论文来源:2019, KDD
论文地址:download
论文代码:download
前言
当前研究 GCN 存在的问题:
- [li]训练大规模的 GCN 存在计算成本昂贵的问题,当前基于 SGD 的算法的计算成本随着 GCN 层数的增长呈现指数增长。【基于消息聚合框架,传播过程看成一颗树】
现有 GCN 训练方法存在的问题:
- [li]Memory requirement
- Time per epoch
- Convergence speed
1 介绍
几种 GCN 类型:
- GCN:Full-batch gradient descent 需要计算整个所有节点的梯度,也需要存储所有 Embedding ,所以导致 $O(NFL)$ 内存需求;
- 在每个 epoch 只更新一次参数,所以 SGD 的收敛速度缓慢;
- memory: bad
- time per epoch: good
- convergence: bad
Mini-batch SGD
-
每次更新只基于一个 mini-batch 的梯度,它可以减少内存需求,并在每个 epoch 执行多次更新,从而加快收敛速度;
-
采用 variance 减少技术来减小邻域采样节点的大小;
2 Cluster-GCN
2.1 Vanilla Cluster-GCN
对于图 $G$ ,把它的节点划分为 $c$ 个群: $V=\left[V_{1}, \ldots, V_{c}\right]$ ,其中 $V_{t}$ 包含在第 $t$ 个群中的节点。根据这些群可以得到 $c$ 个子图:
$\bar{G}=\left[G_{1}, \ldots, G_{c}\right]=\left[V_{1}, E_{1}, \ldots, V_{c}, E_{c}\right]$
其中 $E_{t}$ 只包含 $V_{t}$ 中的节点之间的边。
同样,邻接矩阵会被划分为 $c^{2}$ 个子矩阵 (只需重新排列一下节点的位置) :
$A=\bar{A}+\Delta=\left[\begin{array}{ccc}A_{11} & \cdots & A_{1 c} \\\vdots & \ddots & \vdots \\A_{c 1} & \cdots & A_{c c}\end{array}\right]$
其中,
$\bar{A}=\left[\begin{array}{ccc}A_{11} & \cdots & 0 \\\vdots & \ddots & \vdots \\0 & \cdots & A_{c c}\end{array}\right], \Delta=\left[\begin{array}{ccc}0 & \cdots & A_{1 c} \\\vdots & \ddots & \vdots \\A_{c 1} & \cdots & 0\end{array}\right]$
$A_{t t}$ 表示子图 $G_{t}$ 的邻接矩阵, $A_{s t}$ 表示节点 $V_{s}$ 和节点 $V_{t}$ 之间的边构成的邻接矩阵。特征和标签数据也可以根据群的划分进行相应的划分: $\left[X_{1}, \cdots, X_{c}\right] $ 和 $ \left[Y_{1}, \cdots, Y_{c}\right]$ 。
用 $\bar{A}^{\prime}$ 表示矩阵 $A$ 的标准化后的结果,那么整个 GCN 的卷积过程可以形式化表示为:
$Z^{(L)}=\bar{A}^{\prime} \sigma\left(\bar{A}^{\prime} \sigma\left(\cdots \sigma\left(\bar{A}^{\prime} X W^{(0)}\right) W^{(1)}\right) \cdots\right) W^{(L-1)}$
即:
$\mathrm{Z}^{(L)} =\left[\begin{array}{c}\bar{A}_{11}^{\prime} \sigma\left(\bar{A}_{11}^{\prime} \sigma\left(\cdots \sigma\left(\bar{A}_{11}^{\prime} X_{1} W^{(0)}\right) W^{(1)}\right) \cdots\right) W^{(L-1)} \\\vdots \\\bar{A}_{c c}^{\prime} \sigma\left(\bar{A}_{c c}^{\prime} \sigma\left(\cdots \sigma\left(\bar{A}_{c c}^{\prime} X_{c} W^{(0)}\right) W^{(1)}\right) \cdots\right) W^{(L-1)}\end{array}\right]$
对应的损失函数如下:
$\mathcal{L}_{\bar{A}^{\prime}}=\sum\limits _{t} \frac{\left|\mathcal{V}_{t}\right|}{N} \mathcal{L}_{\bar{A}_{t t}^{\prime}} \quad\quad\text { and }\quad \quad\mathcal{L}_{\bar{A}_{t t}^{\prime}}=\frac{1}{\left|\mathcal{V}_{t}\right|} \sum\limits_{i \in \mathcal{V}_{t}} \operatorname{loss}\left(y_{i}, z_{i}^{(L)}\right)$
在每一步中,对一个聚类 $V_{t}$ 进行采样,然后根据块损失函数的梯度进行 SGD 更新,这只需要当前 batch 上的子图 $A_{t t}$, $X_{t}$, $Y_{t}$ 和模型 $\left\{W^{(l)}\right\}_{l}^{L}$ 。实现只需要矩阵乘积的正向和反向传播,这比以前基于 SGD 的训练方法中使用的邻域搜索过程更容易实现。
利用图的聚类算法对图进行划分,像 Metis[8] 和 Graclus[4] 这样的,目的是在图中的顶点上构造分区,使簇内的边比簇间的边接更多,从而更好地捕获图的聚类和社区结构。
划分簇的意义在于:
- 对于每个 batch 而言,Embedding utilization 相当于簇内的连接。每个节点及其相邻节点通常位于同一簇内,因此经过几次后跳跃后,邻接节点大概率还是在簇内;
- 由于使用 $\bar{A}$ 代替 $A$ ,误差与簇间的的连接 $\Delta$ 成正比,所以需要使得簇间的连接数量尽可能少。
在 Figure 1 中,我们用全图G说明邻域展开,用聚类划分 $\bar{G} $ 说明图。我们可以看到,Cluster-GCN 可以避免大量的邻域搜索,并关注每个集群内的邻居。

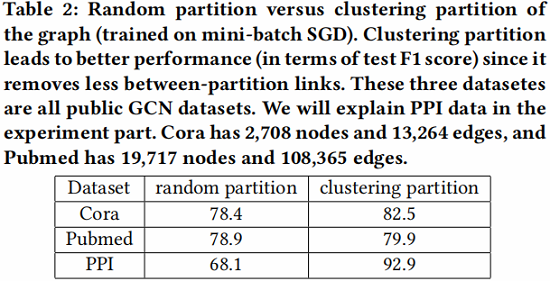
在 Table 2 中,我们展示了两种不同的节点划分策略:随机分区和聚类分区。我们使用随机划分和 METIS 将图分成10个部分。然后使用一个分区作为批处理来执行SGD更新。我们可以看到,在相同数量的时代下,使用聚类划分可以获得更高的精度。这表明使用图聚类是很重要的,分区不应该随机形成。
时间和空间复杂度计算如 Table 1 所示:

2.2 Stochastic Multiple Partitions
虽然普通的 Cluster-GCN 实现了良好的计算和内存复杂度,但仍然有两个潜在的问题:
- [li]在图被分区后,Cluster 之间的连接将被删除。因此,性能可能会受到影响;
- 图的聚类算法往往会将相似的节点聚集在一起。因此,集群的分布可能与原始数据集不同,从而导致在执行SGD更新时对全梯度的有偏估计;
下图为 Reddit 数据集中标签分布不平衡的案例,通过每个簇的标签分布计算其熵值,与随机分割相比,可以清楚的看到聚类分区的簇的熵较小,这表明簇的标签分布偏向于某些特征的标签,所以这会增加不同 batch 的梯度更新的差异,并影响 SGD 的收敛性。
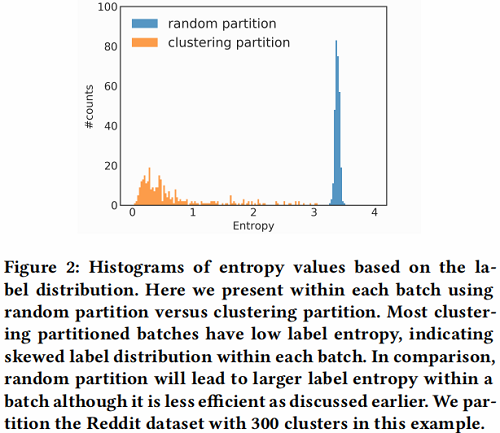
为了解决上述问题,文中提出了一种 Stochastic Multiple Partitions,在簇接之间进行合并,并减少 batch 间的差异(variance) 。作者首先用一个较大 的 $p$ 把图分割成 $ p$ 个簇 $V_{1}, \ldots, V_{p}$ ,然后对于 SGD 的更新重新构建一个 batch $B$,而不是只考虑一个簇。随机地选择 $q$ 个簇,定义为 $t_{1}, \ldots, t_{q} $, 并把它们的节点 $V_{t 1} \cup \ldots \cup V_{t} $ 包含到这个batch $B$ 中。此外,在选择的簇之间的连接
$A_{i j} \mid i, j \in t_{1}, \ldots, t_{q}$
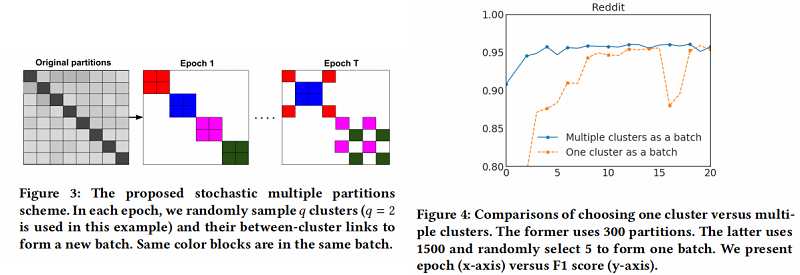
被添加回去。通过这种方式,在簇之间的连接就会被重新合并。这种簇的组合使 batch 之间的差异(variance)更小。图3说明了每个epoch随机选中不同的簇组合成为一个batch。作者在Reddit数据集上进行了一个实验,证明了该方法的有效性。在图4中,可以观察到使用多个簇作为一个batch可以提高收敛性。最后的Cluster-GCN算法在算法1中给出。

之前训练更深的GCNs[9]的尝试似乎表明,添加更多的层是没有帮助的。然而,实验中使用的数据集可能太小,无法进行适当的证明。例如,[9]考虑了一个只有几百个训练节点的图,因此过拟合可能是一个问题。此外,我们观察到,深度GCN模型的优化变得困难,因为它可能会阻碍来自前几层的信息被通过。在[9]中,它们采用了一种类似于残差连接[6]的技术,使模型能够将信息从前一层传输到下一层。具体来说,将第 $l$ 层的隐藏表示添加到下一层中。
$X^{(l+1)}=\sigma\left(A^{\prime} X^{(l)} W^{(l)}\right)+X^{(l)}$
虽然上式似乎是合理的,但无论相邻节点的数量如何,对所有节点使用相同的权重可能是不合适的。此外,当使用更多的层时,数值可能会呈指数增长,这可能会导致数值不稳定。因此,作者提出了上式的修改版本,以更好地维护邻居信息和数值范围。文中也首先向原始 $A$ 添加一个单位矩阵(identity),然后执行标准化(normalization):
$\tilde{A}=(D+I)^{-1}(A+I)$
然后考虑
$X^{(l+1)}=\sigma\left((\tilde{A}+\lambda \operatorname{diag}(\tilde{A})) X^{(l)} W^{(l)}\right)$
采用的“对角增强”技术的实验结果,我们表明这种新的归一化策略可以帮助构建深度GCN和实现SOTA性能。
3 实验
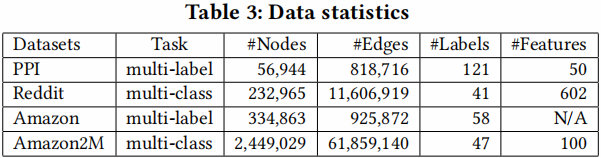
文中评估了所提出的针对四个公共数据集的多标签和多类分类两个任务的GCN训练方法,数据集统计如 Table 3 所示。Reddit数据集是迄今为止为GCN所看到的最大的公共数据集,Amazon2M数据集是由作者自己收集的,比 Reddit 大得多。
3.1 Training Performance for median size datasets
Training Time vs Accuracy
首先,在训练速度方面,作者将所提出的方法与其他方法进行了比较。在图6中,x轴显示了以秒为单位的训练时间,y轴显示了验证集的准确性(F1分数)。作者用2、3、4层GCN绘制了三个数据集的训练时间与准确度的关系图。由于GraphSAGE比VRGCN比文中的方法慢,GraphSAGE的曲线只出现在PPI和Reddit数据集中。可以看到,对于不同层数的GCNs,文中的方法对于PPI和Reddit数据集都是最快的。

对于Amazon数据,由于节点的特征不可用,所以使用一个单位矩阵作为特征矩阵 $X$。在此设置下,参数矩阵 $W^{0}$ 的形状为 334863x128。因此,计算主要是由稀疏矩阵运算带来的,如$AW^{0}$ 。对于三层的情况,文中的方法仍然比VRGCN快,但是对于两层和四层的情况就慢了。原因可能是不同框架的稀疏矩阵运算速度不同。VRGCN是在TensorFlow中实现的,而Cluster-GCN是在PyTorch中实现的,它的稀疏张量支持仍然处于非常早期的阶段。在 Table 6 中,展示了TensorFlow和PyTorch对Amazon数据进行前馈/反向传播操作的时间,并使用一个简单的两层网络对这两个框架进行基准测试。可以清楚地看到TensorFlow比PyTorch快。当隐藏单元的数量增加时,这种差异更为显著。这也许可以解释为什么Cluster-GCN在Amazon dataset中有更长的训练时间。

Memory usage comparison
对于大规模的GCNs的训练,除了训练时间外,训练所需的内存使用往往更为重要,直接限制了可扩展性。内存的使用包括许多epochs训练GCN所需的内存。正如在第3节中讨论的,为了加速训练,VRGCN需要在训练期间保存历史embeddings,因此它需要比Cluster-GCN更多的内存来进行训练。由于指数邻域增长的问题,Graph-SAGE对内存的要求也高于Cluster-GCN。在表5中,比较了不同层的GCN与VRGCN的内存使用情况。当增加层数时,Cluster-GCN的内存使用量并没有增加很多,原因是增加一层时引入的额外变量是权矩阵 $W^{L}$ ,与子图和节点特征相比,权重矩阵$W^{L}$ 相对较小。而VRGCN需要保存每一层的历史embeddings,而embeddings通常是密集的,很快就会控制内存的使用。从表5可以看出,Cluster-GCN的内存效率比VRGCN高得多。例如,在Reddit数据上,要训练一个4层的隐藏维度为512的GCN,VRGCN需要2064MB内存,而Cluster-GCN只需要308MB内存。

3.2 Experimental results on Amazon2M
A new GCN dataset: Amazon2M
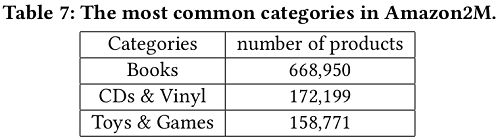
到目前为止,用于测试GCN的最大公共数据是Reddit dataset,其统计数据如 Table 3所示,其中包含大约200K个节点。如 Figure 6 所示,对该数据的GCN训练可以在几百秒内完成。为了测试GCN训练算法的可扩展性,作者基于Amazon co-purchase network构建了一个更大的图,包含超过200万个节点和6100万条边[11,12]。原始的共同购买( co-purchase)数据来自Amazon-3M。在图中,每个节点都是一个产品,图中边的连接表示是否同时购买两个产品。每个节点特征都是通过从产品描述中的bag-of-word式的特征,然后进行主成分分析[7]生成的,将维数降为100。此外,我们使用top-level categories作为该产品/节点的标签(最常见的类别见 Table 7 。数据集的详细统计数据如 Table 3 所示。

在 Table 8 中,作者比较了不同层次GCNs的VRGCN在训练时间、内存使用和测试准确度(F1分数)方面的差异。从表中可以看出
- 训练两层GCN的VRGCN比Cluster-GCN快,但是却慢于增加一层网络但实现相似准确率的Cluster-GCN
- 在内存使用方面,VRGCN比Cluster-GCN使用更多的内存(对于三层的情况5倍多)。当训练4层GCN的时候VRGCN将被耗尽,然而Cluster-GCN当增加层数的时候并不需要增加太多的内存,并且Cluster-GCN对于这个数据集训练 4 层的GCN将实现最高的准确率。

3.3 Training Deeper GCN
在本节中,作者考虑了具有更多层的GCNs。首先在 Table 9中显示了Cluster-GCN和VRGCN的时间比较。PPI数据集用于基准测试,实验中对这两种方法运行了200个epoch。结果发现VRGCN的运行时间由于其代价很大的邻域查找而呈指数增长,而Cluster-GCN的运行时间只呈线性增长。

接下来作者研究了使用更深层次的GCNs是否能获得更好的精度。在3.3节,文中讨论了修改邻接矩阵A的不同策略,以方便对深度GCNs的训练。文中将对角增强技术应用于深度GCNs,并对PPI数据集进行了实验研究。结果如 Table 11 所示。对于2-5层的情况,所有方法的精度都随着层数的增加而提高,这表明更深层的GCNs可能是有用的。然而,当使用7或8个GCN层时,前三种方法无法在200个epoch内收敛,导致精度显著下降。一个可能的原因是对更深层GCNs的优化变得更加困难。文中在 Figure 5 中显示了一个8层GCN的详尽的收敛。采用所提出的对角增强技术(11),可以显著提高收敛性,达到相似的精度。


State-of-the-art results by training deeper GCNs
通过对Cluster-GCN的设计和提出的归一化方法,现在可以对GCNs进行更深入的训练,从而获得更高的精度(F1分)。文中将测试精度与表10中其他现有方法进行了比较。对于PPI数据集,Cluster-GCN可以通过训练一个包含2048个隐藏单元的5层GCN来达到最先进的效果。对于Reddit数据集,使用了一个包含128个隐藏单元的4层GCN。

4 Conclusion
此文提出了一种新的训练算法Cluster-GCN。实验结果表明,该方法可以在大型图上训练非常深的GCN,例如在一个超过200万个节点的图上,使用2G左右的内存训练时间不到1小时,精度达到90.41 (F1 score)。使用该方法,能够成功地训练更深入的GCNs,它可以在PPI数据集和Reddit数据集上获得最先进的测试F1 score。
- 深度学习论文随记(二)---VGGNet模型解读-2014年(Very Deep Convolutional Networks for Large-Scale Image Recognition)
- 论文解读| Very Deep Convolutional Networks for Large-Scale Image Recognition
- VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION 这篇论文
- 《Very Deep Convolutional Networks for Large-Scale Image Recognition》论文阅读
- VGG-16、VGG-19(论文阅读《Very Deep Convolutional NetWorks for Large-Scale Image Recognition》)
- VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION论文翻译
- 【论文精读】Select Via Proxy: Efficient Data Selection For Training DeepNetworks
- 【论文解读】Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition
- 【论文解读】 FPGA实现卷积神经网络CNN(一): CNP: AN FPGA-BASED PROCESSOR FOR CONVOLUTIONAL NETWORKS
- VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION 论文学习
- [论文解读] MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications
- [论文解读] ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices
- 【Paper Note】Very Deep Convolutional Networks for Large-Scale Image Recognition——VGG(论文理解)
- Very Deep Convolutional Networks for Large-Scale Image Recognition—VGG论文翻译—中文版
- 论文解读(Geom-GCN)《Geom-GCN: Geometric Graph Convolutional Networks》
- 论文笔记 | VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE -SCALE IMAGE RECOGNITION
- An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling 论文理解
- [深度学习论文笔记][Image Classification] Very Deep Convolutional Networks for Large-Scale Image Recognitio
- [论文解读]VGGNet:Very Deep Convolution Networks for Large-Scale Image Recognition
- VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION论文翻译
