Junyuan Xie, Ross B. Girshick, Ali Farhadi
2015, ICML
1243 Citations, 45 References
Code:Download
Paper:Download

Abstract

　　在本文中，我们提出了 Deep Embedded Clustering(DEC)，一种使用深度神经网络同时学习 feature representations 和 cluster assignments 的方法。DEC学习从数据空间到低维特征空间的映射，并在其中迭代地优化聚类目标。

1. Introduction

　　What is Clustering???

　　Some questions for Clustering in unsupervised methods: 

• [li]What defifines a cluster?
• What is the right distance metric?
• How to effificiently group instances into clusters?
• How to validate clusters?

[/li] 　　DEC的目的：本文希望找到一种方案，可以联合解决特征空间学习与聚类关系判别。本文的 idea 是从一篇 CV 论文中获得的，但是该论文采用的是监督学习的方法，然而 DEC 是无监督方法。   　　本文定义了一个从 data space $X$ 到 lower-dimensional feature space $Z$ 的参数化 non-linear mapping ，在其中优化了一个聚类目标。之前的工作主要在数据空间或浅层线性嵌入空间上操作，本文通过在聚类目标上的反向传播使用随机梯度下降(SGD)来学习映射，这是由深度神经网络参数化的。本文将这种聚类算法称为 Deep Embedded Clustering ，或DEC。

　　本文贡献：

1. [li]joint optimization of deep embedding and clustering;
2. a novel iterative refifinement via soft assignment; 
3. state-of-the-art clustering results in terms of clustering accuracy and speed.

[/li]

2. Related work

　　聚类在机器学习的  feature selection、distance functions、grouping methods 以及 cluster valida ad8 tion 方面得到了广泛研究。

　　流行的聚类方法的一个分支是 kmeans 和高斯混合模型(GMM)。这些方法速度快，可适用于范围广泛的问题。然而，它们的距离度量仅限于原始数据空间，当输入维数较高时，它们往往会无效。

　　Spectral clustering 及其变体最近得到了受欢迎。它们允许更灵活的距离度量，并且通常比 kmeans 表现得更好。Yang等人已经探索了 spectral clustering 和 embedding 的结合。 Tian 等人提出了一种基于 spectral clustering 的算法，但用深度自编码器代替特征值分解，提高了性能，但进一步增加了内存消耗。

　　Spectral clustering algorithms 需要计算全图的  Laplacian matrix ，因此在数据点的数量上具有二次或超二次复杂度。

　　最小化 data distribution 和 embedded distribution 之间的 KL   差异。 

　　我们从参数化的  $t-SNE$  中获得灵感。我们定义了一个 centroid-based  的概率分布，并最小化其  $KL$  散度到辅助目标分布，以同时改进聚类分配和特征表示，而不是最小化  $KL$  散度以产生辅助目标分布，从而产生忠实于原始数据空间中距离的嵌入。基于质心的方法也有将复杂度降低到  $O(nk)$  的好处，其中  $k$  是质心的数量。

3. Deep embedded clustering

　　Consider the problem of clustering a set of  $n$  points  $\left\{x_{i} \in\right.   X\}_{i=1}^{n} $ into  $k$  clusters, each represented by a centroid  $\mu_{j}$, $j=1, \ldots, k $. Instead of clustering directly in the data space  $X$ , we propose to first transform the data with a nonlinear mapping  $f_{\theta}: X \rightarrow Z$ , where  $\theta$  are learnable parameters and  $Z $ is the latent feature space. The dimensionality of  $Z$  is typically much smaller than  $X$  in order to avoid the "curse of dimensionality" (Bellman, 1961). To parametrize  $f_{\theta}$ , deep neural networks (DNNs) are a natural choice due to their theoretical function approximation properties (Hornik, 1991) and their demonstrated feature learning capabilities (Bengio et al., 2013). < 56c div>　　The proposed algorithm (DEC) clusters data by simultaneously learning a set of  $k$  cluster centers  $\left\{\mu_{j} \in Z\right\}_{j=1}^{k}$  in the feature space  $Z$  and the parameters  $\theta$  of the DNN that maps data points into  $Z$ . DEC has two phases: (1) parameter initialization with a deep autoencoder (Vincent et al., 2010) and (2) parameter optimization (i.e., clustering), where we iterate between computing an auxiliary target distribution and minimizing the Kullback-Leibler (KL) divergence to it. We start by describing phase (2) parameter optimization  clustering, given an initial estimate of  $\theta$  and  $\left\{\mu_{j}\right\}_{j=1}^{k} $.

3.1. Clustering with KL divergence

　　给定非线性映射  $f_{\theta}$  和初始聚类质心 $ \left\{\mu_{j}\right\}_{j=1}^{k}$  的初始估计，我们建议改进聚类使用在两个步骤之间交替的无监督算法。 第一步，我们计算  embedded points  和  cluster centroids  之间的  soft assignment 。 第二步，我们更新深度映射  $f_{\theta}$  并通过使用辅助目标分布从当前的高 ad0 置信度分配中学习来细化集群质心。 重复此过程，直到满足收敛标准。

3.1.1. Soft assignment 

　　我们使用 Student’s t-distribution 作为核来衡量 embedded point  $z_i$  和质心  $\mu_{j}$  之间的相似性：

　　　　$q_{i j}=\frac{\left(1+\left\|z_{i}-\mu_{j}\right\|^{2} / \alpha\right)^{-\frac{\alpha+1}{2}}}{\sum_{j^{\prime}}\left(1+\left\|z_{i}-\mu_{j^{\prime}}\right\|^{2} / \alpha\right)^{-\frac{\alpha+1}{2}}} \quad \quad\quad\quad (1)$

　　其中：$z_{i}=f_{\theta}\left(x_{i}\right) \in Z$  是嵌入后的  $x_{i} \in X$  ，$\alpha$  是  Student's  t  distribution 的自由度，$q_{i j}$  可以解释为将样本 $i$ 分配给聚类 $j$ 的概率（即软分配）。由于我们不能在无监督设置下的验证集上交叉验证  $\alpha $，并且学习它是多余的，我们让  $α=1$  用于所有实验。

3.1.2. KL Divergence minimization

　　我们建议在  auxiliary target distribution 的帮助下，通过学习  high confidence assignments 来迭代地细化  clusters 。具体来说，我们的模型是通过匹配软分配到目标分布来训练的。为此，我们将我们的目标定义为软分配  $q_i$  和辅助分布  $p_i$  之间的KL散度损失如下：

　　　　$L=\mathrm{KL}(P \| Q)=\sum \limits_{i} \sum \limits_{j} p_{i j} \log \frac{p_{i j}}{q_{i j}} \quad \quad\quad\quad (2)$

　　目标分布  $P$  的选择是  DEC  的性能的关键。一种简单的方法是将超过置信阈值的数据点的每个  $p_i$  设置为一个  $delta$  分布（到最近的质心），而忽略其余的。然而，由于  $q_i$  是软任务，所以使用较软的概率目标更自然和灵活。

　　具体来说，我们希望我们的  target distribution  具有以下特性：

1. strengthen predictions (i.e., improve cluster purity).
2. put more emphasis on data points assigned with high confidence.
3. normalize loss contributio 3ba4 n  of each centroid to prevent large clusters from distorting the hidden feature space.

　　在我们的实验中，我们计算  $p_i$，首先将  $q_i$  提高到二次幂，然后按每个簇的频率归一化：

　　　　${\large p_{i j}=\frac{q_{i j}^{2} / f_{j}}{\sum_{j^{\prime}} q_{i j^{\prime}}^{2} / f_{j^{\prime}}}} \quad \quad\quad\quad (3)$

　　其中  $f_{j}=\sum \limits _{i} q_{i j}$   是 soft cluster frequencies 。关于L和P的经验性质的讨论，请参考第5.1节。

3.1.3. Optimization

　　我们利用具有动量的随机梯度下降(SGD)联合优化了聚类中心  $\left\{\mu_{j}\right\} $  和DNN参数  $\theta  $。$L$ 对每个数据点  $z_i$  和每个聚类质心  $\mu_{j}$  的特征空间嵌入的梯度计算为：

　　　　$\frac{\partial L}{\partial z_{i}}=\frac{\alpha+1}{\alpha} \sum \limits _{j}\left(1+\frac{\left\|z_{i}-\mu_{j}\right\|^{2}}{\alpha}\right)^{-1}\quad \quad\quad\quad (4)$

　　　　$\frac{\partial L}{\partial \mu_{j}}=-\frac{\alpha+1}{\alpha} \sum \limits _{i}\left(1+\frac{\left\|z_{i}-\mu_{j}\right\|^{2}}{\alpha}\right)^{-1}\times\left(p_{i j}-q_{i j}\right)\left(z_{i}-\mu_{j}\right)\quad \quad\quad\quad (5)$

　　梯度  $\partial L / \partial z_{i}$  然后被传递给DNN，并用于标准的反向传播来计算  DNN  的参数梯度  $\partial L / \partial \theta$。为了发现集群分配，当连续两次迭代之间改变集群分配的点小于  $tol  \%$  时，我们停止我们的过程。

3.2. Parameter initialization

　　到目前为止，我们已经讨论了  DEC  如何处理  DNN  参数$θ$  和簇质心  ${µ_j}$  的初始估计。现在我们将讨论参数和质心是如何初始化的。

　　我们使用堆叠自动编码器(SAE)初始化DEC，因为最近的研究表明，它们在真实数据集上始终产生具有语义意义和分离良好的表示。因此，SAE学习到的无监督表示自然地促进了使用DEC进行聚类表示的学习。

　　我们一层一层地初始化SAE网络，每一层都是一个去噪自动编码器，在随机损坏后重建前一层的输出。去噪自动编码器是一种两层神经网络，其定义为：

　　　　$\tilde{x} \sim \operatorname{Dropout}(x) \quad \quad\quad\quad (6)$

　　　　$h=g_{1}\left(W_{1} \tilde{x}+b_{1}\right) \quad \quad\quad\quad (7)$

　　　　$\tilde{h} \sim \operatorname{Dropout}(h) \quad \quad\quad\quad (8)$

　　　　$y=g_{2}\left(W_{2} \tilde{h}+b_{2}\right)\quad \quad\quad\quad (9)$

　　其中，$\operatorname{Dropout}(\cdot)$  是一个随机映射，它将其输入维度的一部分随机设置为0，$g_{1}$  and  $g_{2}$ 分别为编码层和解码层的激活函数，$\theta=\left\{W_{1}, b_{1}, W_{2}, b_{2}\right\}$  为模型参数。训练是通过最小化最小二乘损失  $\|x-y\|_{2}^{2}$  来完成的。在训练了一层后，我们使用它的输出有输入来训练下一层。我们在所有编码器/解码器对中使用校正线性单元(ReLUs)，除了第一对的  $g_{2}$ （它需要重建可能有正负值的输入数据，如零均值图像）和最后对的  $g_{1}$  (因此最终数据嵌入保留完整信息)。

　　经过  greedy layer-wise training  后，我们将所有编码器层和所有解码器层，按反向层训练顺序连接起来，形成一个深度自动编码器，然后对其进行微调，使其最小化重构损失。最终的结果是一个中间有一个瓶颈编码层的多层深度自动编码器。然后我们丢弃解码器层，并使用编码器层作为数据空间和特征空间之间的初始映射，如 Fig. 1 所示。

　　　　

　　为了初始化聚类中心，我们将数据通过初始化的DNN传递，得到嵌入的数据点，然后在特征空间  $Z$  中执行标准的  $k-means$  聚类，得到  $k$  个初始质心  $\left\{\mu_{j}\right\}_{j=1}^{k}$。

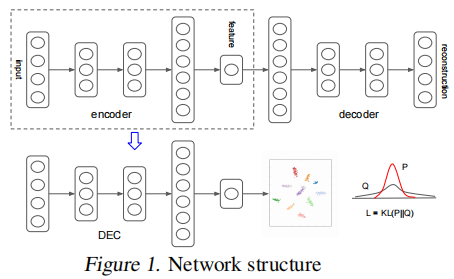
4. Experiments

4.1. Datasets

　　我们在一个文本数据集和两个图像数据集上评估了所提出的方法(DEC)，并将其与其他算法包括  $k-means$、$LDGMI$ 和  $SEC$  进行比较。$LDGMI$  和$SEC$  是基于  spectral clustering  的算法，它们使用拉普拉斯矩阵和各种变换来提高聚类性能。

• MNIST：MNIST数据集由280000像素大小的70000个手写数字组成。这些数字居中并进行尺寸归一化(LeCun等，1998)。
• STL-10: 96 x 96彩色图像的数据集。有10个类别，每个类别有1300个样本。它还包含100000张相同分辨率的无标签图像(Coates等，2011)。训练自动编码器时，我们还使用了无标签的集合。与Doersch等人(2012)相似，我们将HOG特征和8×8色图连接起来，用作所有算法的输入。
• REUTERS: REUTERS包含大约810000个以类别树标签的英语新闻报道(Lewis等，2004)。我们使用了四个根类别：公司/工业，政府/社会，市场和经济学作为标签，并进一步修剪了由多个根类别标签的所有文档以得到685071个文章。然后，我们根据2000个最常见的词干计算tf-idf特征。由于某些算法无法扩展到整个Reuters数据集，因此我们还抽样了10000个样本的随机子集，我们将其称为REUTERS-10k，以进行比较。

　　　　

4.2. Evaluation Metric

　　我们使用标准的无监督评估  metric  和   protocol  来与其他算法进行评估和比较。对于所有的算法，我们将聚类的数量设置为 ground-truth  类别的数量，并以无监督的聚类精度(ACC)来评估性能：

　　　　$A C C=\max _{m} \frac{\sum_{i=1}^{n} 1\left\{l_{i}=m\left(c_{i}\right)\right\}}{n}\quad \quad\quad\quad (10)$

　　其中 $ l_{i}$  是ground-truth label ，$c_{i}$ 是该算法产生的聚类分配，$m$ 是将  $c_{i}$ 进行聚类映射。

4.3. Implementation

　　实验参数补充，略........

4.4. Experiment results

　　我们定量和定性地评估了我们的算法的性能。在 Table 2 中，我们报告了每种算法的最佳性能，超过9个超参数设置。

　　　　

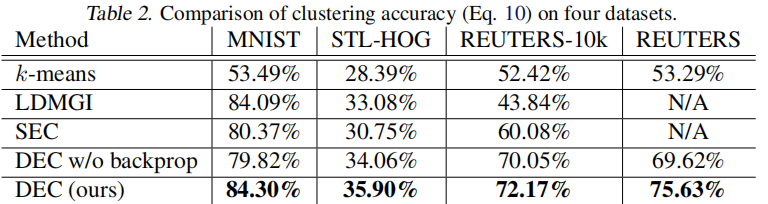
　　请注意，DEC的性能优于所有其他方法，有时会有很大的优势。为了证明端到端训练的有效性，我们还展示了在聚类过程中冻结非线性映射  $f_θ$  的结果。

　　为了研究超参数的影响，我们绘制了每种方法在所有 $9$ 种设置下的准确性（ Fig.2）。

　　　　

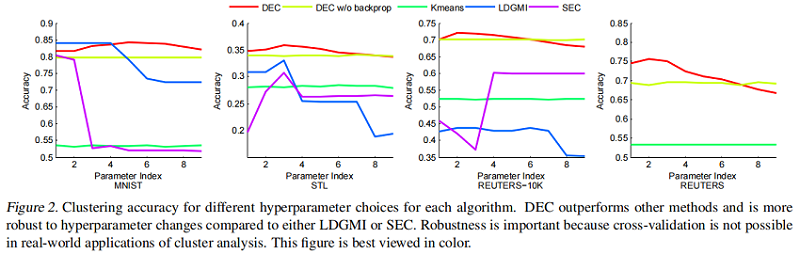
 　　我们观察到，与  LDGMI  和  SEC  相比，DEC  在超参数范围内更为一致。对于  DEC，超参数  $λ=40$  在所有数据集上都给出了接近最优的性能，而对于其他算法，最优超参数变化很大。此外，DEC可以用GPU加速处理整个  REUTERS  数据集，而第二好的算法LDGMI和SEC则需要数月的计算时间和 TB 的内存。事实上，我们不能在完整的  REUTERS  数据集上运行这些方法，并在  Table 2  中报告N/A(这些方法的GPU适应不是重要的)。

　　

 　　在  Fig. 3  中，我们显示了  MNIST  和  STL  中每个聚类中10张得分最高的图像。每一行对应一个  cluster，图像根据它们到  cluster center  的距离从左到右进行排序。我们观察到，对于  MNIST，DEC  的  cluster assignment  很好地对应自然集群，除了混淆4和9，而对于STL，DEC对飞机、卡车和汽车大多是正确的，但在动物类别时，部分注意力花在姿势上而不是类别上。

5. Discussion

5.1. Assumptions and Objective

　　DEC的基本假设是，初始分类器的高置信度预测大部分是正确的。为了验证该假设对我们的任务是否成立，以及我们对  $P$  的选择是否具有所需的属性，我们针对每个嵌入点  $\left|\partial L / \partial z_{i}\right|$  ，对其软分配  $q_{ij}$  ，绘制了  $L$  的梯度大小到随机选择的  MNIST  聚类  $j$(Fig4)。

　　　　

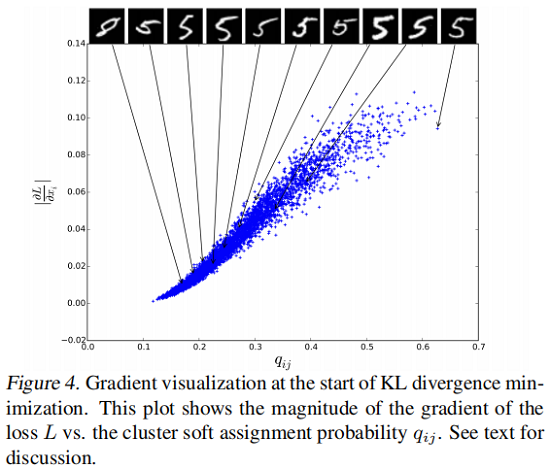
 　　我们观察到靠近聚类中心(较大  $q_{ij}$  )的点对梯度的贡献更大。我们还显示了按  $q_{ij}$   排序的每个10个百分位数的10个数据点的原始图像。如相似度更高的实例“ 5”。随着置信度的降低，实例变得更加模棱两可，最终变成错误标签的 ”8”，表明我们的假设是正确的。

5.2. Contribution of Iterative Optimization

　　在  Fig.5  中，我们可视化了训练过程中  MNIST  随机子集的嵌入式表示的进度。为了可视化，我们将  t-SNE应用于嵌入点  $z_i$。显然，聚类之间的隔离度越来越高。 Fig.5(f)  显示了在SGD epoch  相对应的精度如何提高。

　　

5.3. Contribution of Autoencoder Initialization

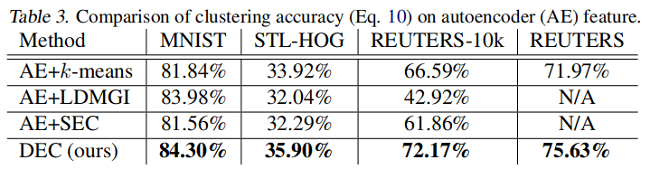
　　为了更好地理解每个组件的贡献，我们在 Table 3 中展示了所有具有自编码器特征的算法的性能。我们观察到，SEC  和  LDMGI  的表现并没有随  autoencoder feature  而显著变化，而  $k-means$  有所改善，但仍低于  $DEC$  。这证明了采用提议的  $KL$  散度目标进行深度嵌入的能力以及微调的好处。

　　　　

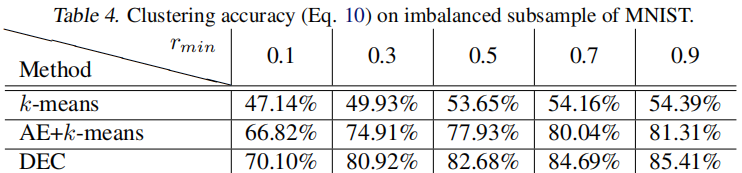
5.4. Performance on Imbalanced Data

　　为了研究不平衡数据的影响，我们对具有不同保留率的  MNIST  子集进行了采样。对于最小保留率  $r_{\min } $，类别  $0$  的数据点将以  $r_{\min } $的概率保留，类别  $9$  将以  $1$  的概率保留，而其他类别的数据点之间则保持线性关系。结果，最大的簇将是最小簇的  $1 / r_{\min }$  倍。从  Table 4  中我们可以看到  DEC  对于簇大小的变化具有相当强的鲁棒性。我们还观察到，在自动编码器和  k-means  初始化（显示为AE+k-means）之后，KL散度最小化(DEC)不断提高了聚类精度。

　　　　

5.5. Number of Clusters

 　　到目前为止，我们已经假定给出自然簇的数量是为了简化算法之间的比较。但是，实际上，此数量通常是未知的。因此，需要一种确定最佳簇数的方法。为此，我们定义两个度量：

• 标准度量，归一化互信息(NMI)，用于评估具有不同聚类数量的聚类结果：

　　　　$N M I(l, c)=\frac{I(l, c)}{\frac{1}{2}[H(l)+H(c)]}$

　　其中  $I$  是互信息度量，$H$ 是熵。

• 泛化性(G)定义为训练损失与验证损失之间的比率：

　　　　$G=\frac{L_{\text {train }}}{L_{\text {validation }}}$

　　当训练损失低于验证损失时，$G$  很小，这表明高度过拟合。

　　 Fig. 6  显示了当簇数从  $9$ 增加到  $10$  时，泛化性急剧下降，这表明  $9$ 是最优的簇数。我们确实观察到NMI得分最高为  $9$，这表明泛化性是选择簇数的良好指标。 NMI最高是  $9$，而不是  $10$，因为  $9$  和  $4$  在文字上相似，DEC认为它们应该组成一个聚类。这与我们在  Fig. 3  中的定性结果非常吻合。

　　　　

6. Conclusion

　　本文提出了深度嵌入式聚类，即DEC，一种在联合优化的特征空间中聚集一组数据点的算法。DEC的工作原理是迭代优化基于KL散度的聚类目标和自训练目标分布。我们的方法可以看作是半监督自我训练的无监督扩展。我们的框架提供了一种方法来学习专门的 ad8 表示，而没有基本聚类成员标签。

　　实证研究证明了我们所提出的算法的有效性。DEC提供了更好的性能和鲁棒性，这在无监督任务中尤其重要，因为交叉验证是不可能的。DEC还具有数据点数量的线性复杂性的优点，这使得它可以扩展到大型数据集。

『总结不易，加个关注呗！』