数据结构与算法（十二）——算法-动态规划

一、青蛙跳台阶&斐波那契数列

1、问题

　　一只青蛙跳台阶，每次可以跳 1 层或 2 层。青蛙跳到 n 层一共有多少种跳法？

2、思想

　　先把问题规模缩小，考虑 n = 1时，n = 2的解。那么，显然有：

　　（1）边界条件：dp[1] = 1、dp[2] = 2
　　（2）再考虑 n = 3时，逆向思维一下，要跳 3 层，是不是只能是从第 2 阶跳 1 层到或者是从第 1 阶跳 2 层到。所以dp[3] = dp[2] + dp[1]。
　　（3）同理n = 4时，是不是也是只能是从第 3 阶跳 1 层到或者是从第 3 阶跳 2 层到。所以dp[4] = dp[3] + dp[2]。
　　（3）……
　　（4）同理可得，状态转移方程：dp
= dp[n - 1] + dp[n - 2]。

public class Knapsack {
private Goods[] goods;
// 背包的容量
private int c;
// dp[i][j]:表示在前i个物品中选择,能够装入容量为j的背包中的最大价值
private int[][] dp;
private int[][] path;

public Knapsack(Goods[] goods, int c) {
if (goods == null || goods.length == 0 || c <= 0) {
return;
}
this.goods = goods;
this.c = c;

this.dp = new int[goods.length][c + 1];
this.path = new int[goods.length][c + 1];

// 初始化第一列、第一行为0.可不写,默认就是0
//        for (int i = 0; i < dp.length; i++) {
//            dp[i][0] = 0;
//        }
//        for (int i = 0; i < dp[0].length; i++) {
//            dp[0][i] = 0;
//        }
}

// 动态规划
public void dp() {
for (int i = 1; i < dp.length; i++) {
for (int j = 1; j < dp[0].length; j++) {
// 表明当前物品放不了背包
if (goods[i].weight > j) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(dp[i - 1][j], goods[i].value + dp[i - 1][j - goods[i].weight]);

// 用于记录物品选择策略
if (dp[i - 1][j] < goods[i].value + dp[i - 1][j - goods[i].weight]) {
path[i][j] = 1;
}
}
}
}

}

// 获取物品的选择策略
public List<Goods> getPlan() {
// 1.查看 dp 填写情况
for (int i = 0; i < dp.length; i++) {
for (int j = 0; j < dp[i].length; j++) {
System.out.print(dp[i][j] + " ");
}
System.out.println();
}

// 2.物品选择策略
List<Goods> result = new ArrayList<>();
int i = path.length - 1;
int j = path[0].length - 1;
// 从path的最后一个开始找
while (i > 0 && j > 0) {
if (path[i][j] == 1) {
result.add(goods[i]);

j = j - goods[i].weight;
}
i--;
}
return result;
}
}

// 物品
class Goods {
public String name;
// 物品重量
public int weight;
// 物品价值
public int value;

public Goods(String name, int weight, int value) {
this.name = name;
this.weight = weight;
this.value = value;
}

@Override
public String toString() {
return "Goods{" +
"name='" + name + '\'' +
", weight=" + weight +
", value=" + value +
'}';
}
}

public class Main {
public static void main(String[] args) {
Goods[] goods = new Goods[4];

// 为了使得 goods[1] 是第1个物品
goods[0] = null;
goods[1] = new Goods("吉他", 1, 1500);
goods[2] = new Goods("音响", 4, 3000);
goods[3] = new Goods("电脑", 3, 2000);

// 背包容量
final int C = 4;
Knapsack knapsack = new Knapsack(goods, C);
System.out.println("动态规划dp:");
knapsack.dp();

final List<Goods> plan = knapsack.getPlan();
System.out.println("物品选择策略:");
System.out.println(plan);
}
}

// 结果
动态规划dp:
0 0 0 0 0
0 1500 1500 1500 1500
0 1500 1500 1500 3000
0 1500 1500 2000 3500
物品选择策略:
[Goods{name='电脑', weight=3, value=2000}, Goods{name='吉他', weight=1, value=1500}]

4、说明

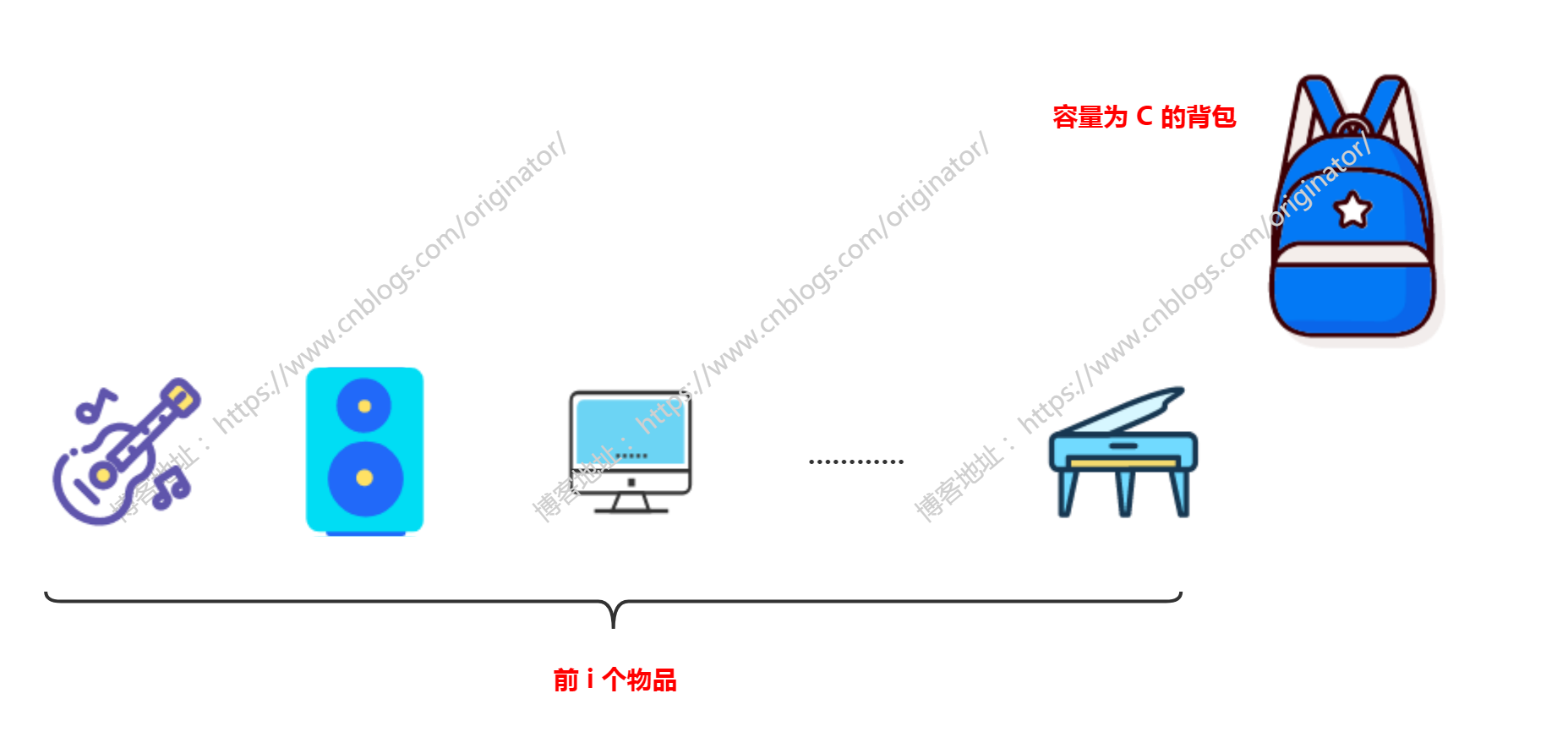
　　不妨假设，在这前 i 个物品中，选取总重量不超过背包容量 C 的物品，且使得物品总价值最大。选择策略叫方案A，此时的最大总价值设为 maxValue。这里理解一下前 i 个物品，由于动态规划问题是规模逐渐增大的，所以，要姑且把物品看成是"有序的"。

　　那么，我们思考一个问题，如果此时来了第 i + 1个物品（价值：V，重量：W），会怎么样呢？如图：

　　主要分为两种情况谈论：
　　1、W > C ：第 i + 1 个物品（钻石）不可取。那么，此时（总体物品是 i + 1个，但是）是不是就相当于没有第 i + 1 这个物品（因为在i + 1个物品中选择，不会取到第 i + 1这个物品），问题的解，是不是就等价于图一（在 i 个物品中选择，背包容量为C），所以，就是方案A，最大总价值就是 maxValue。
　　2、W <= C ：第 i + 1个物品（钻石）可取。又分为两种情况：即拿或不拿。（注：这是0-1背包，一个物品要么不选择，要么只选择一次）
　　　　2.1：不拿。同样，此时（这种情况下）问题的解，与上述（W > C）相同，即方案A，最大总价值就是 maxValue
　　　　2.2：拿。那么，第 i + 1 个物品（钻石）已经被选择了，此时背包容量还有（C - W）。由于第 i + 1个物品已经被选择了，此时问题规模，就是在前 i 个物品中，选取总重量不超过背包容量 C - W 的物品。价值就是dp[i][c - w]。
　　由于2.1和2.2属于一种情况。所以整个问题的解就是 max( maxValue， V + dp[i][c - w] )。

　　下面，再对上面填表的过程，以及代码做一些解释：