命题逻辑

命题与公式

1.命题

一句有真假意义的话（陈述句），记作P。不能是悖论、祈使句、疑问句、感叹句

命题的否定：记以 $\lnot$P

2.析取

P$\lor$Q 读作“P或Q” 真值规定：P$\lor$Q是真的当且仅当P，Q中至少有一个是真的。注意可兼或。

3.合取

P$\land$Q 读作“P且Q” 真值规定：P$\land$Q是真的当且仅当P和Q都是真的。

4.蕴涵

P$\rightarrow$Q 读作“P蕴涵Q” 真值规定： P$\rightarrow$Q是假的当且仅当P是真的而Q是假的。

5.等价

P$\leftrightarrow$Q 读作“P等价Q” 真值规定：P$\leftrightarrow$Q是真的当且仅当P，Q或者都是真的，或者都是假的。

例子：

除非他以书面或口头的方式正式通知我，否则我不参加明天的会议。

令P：他书面通知我； Q：他口头通知我； R：我参加明天的会议。

于是，上述语句可表示为(P$\lor$Q)$\leftrightarrow$R。

6.命题符号称为原子。

例如，Q，S，…等都是原子。

7.命题公式

命题逻辑中的公式，是如下定义的一个符号串： (1) 原子是公式； (2) 0、1是公式； (3) 若G，H是公式，则($\lnot$G)，(G$\lor$H)， (G$\land$H)，(G$\rightarrow$H)，(G$\leftrightarrow$H)是公式； (4) 所有公式都是有限次使用(1)，(2)，(3)得到的符号串。

规定：

公式(\lnot G)的括号可以省略，写成$\lnot$G。 整个公式的最外层括号可以省略。 五种逻辑联结词的优先级按如下次序递增：\leftrightarrow \rightarrow \land \lor \lnot

8.解释

第一种写法：I1：\frac{P\,\, Q\,\,}{1 0}

第二种写法：{P，\lnot Q}

第三种写法：语言描述，P取1，Q取0

错误写法：P=1，Q=0

9.真值表

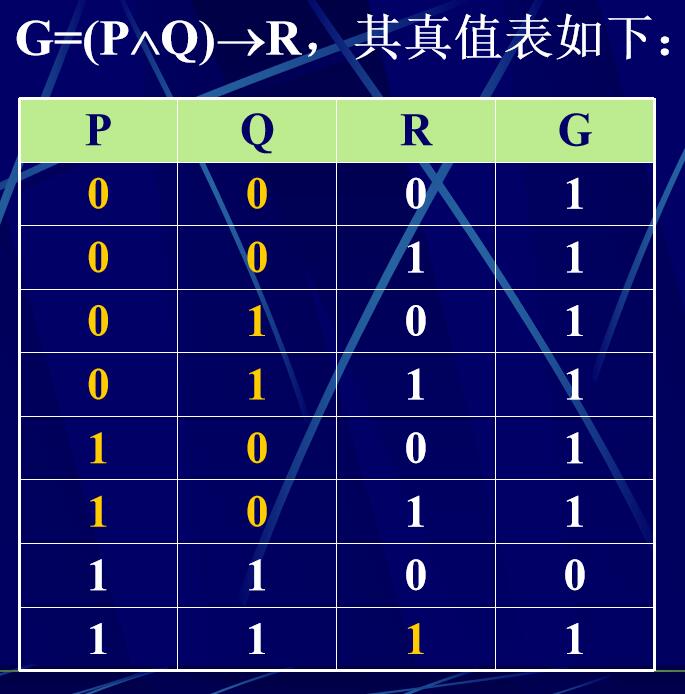
10.恒真、恒假、可满足

公式G称为恒真的(或有效的)，如果G在它的所有解释下都是真的； 公式G称为恒假的(或不可满足的)，如果G在它的所有解释下都是假的； 公式G称为可满足的，如果它不是恒假的

如果公式G在解释I下是真的，则称I满足G； 如果G在解释I下是假的，则称I弄假G

命题公式的等价关系和蕴涵关系

1.公式的等价

公式G，H等价 iff 公式G$\leftrightarrow$H恒真。 公式间的等价关系有自反性、对称性、传递性。

基本等价式

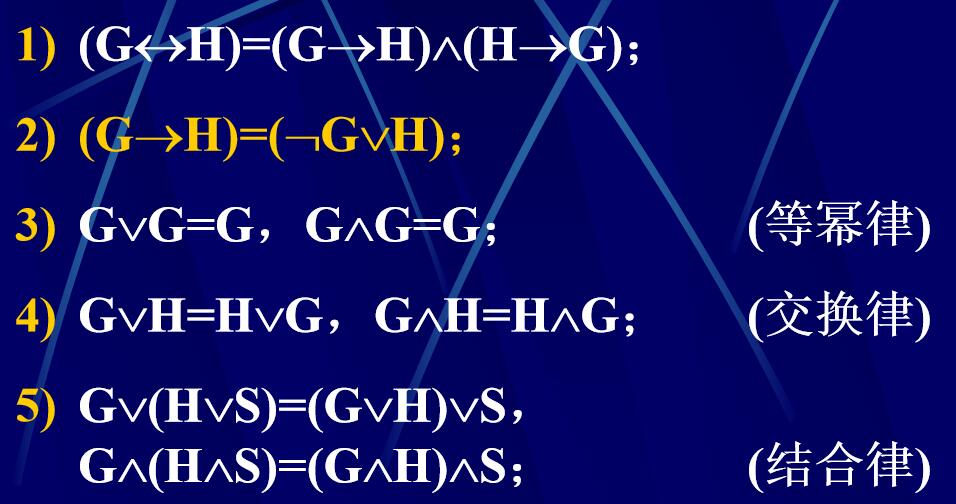
证明命题公式恒真或恒假的两个方法

方法一. 真值表方法。

方法二. 以基本等价式为基础，通过反复对一个公式的等价代换，使之最后转化为一个恒真式或恒假式，从而实现公式恒真或恒假的证明。

2.完备集

设Q是逻辑运算符号集合，若所有逻辑运算都能由Q中元素表示出来，而Q的任意真子集无此性质，则称Q是一个完备集。

核心步骤：取两次反

3.与非式

命题 “P与Q的否定”称为P与Q的与非式，记作P$\uparrow$Q。

真值规定:P$\uparrow$Q为真 iff P,Q不同时为真。

备注：$\uparrow$是一个完备集

4.或非式

命题 “P或Q的否定”称为P与Q的或非式，记作P$\downarrow$Q

真值规定：P$\downarrow$Q为真 iff P，Q同时为假。

备注：$\downarrow$是一个完备集

5.公式的蕴涵

定理：设G，H是两个公式。 称H是G的逻辑结果(或称G蕴涵H)，当且仅当对G，H的任意解释I，如果I满足G，则I也满足H，记作G$\Rightarrow$H。

是一种部分序关系（自反、反对称、传递）

G$\Rightarrow$H当且仅当G$\rightarrow$H是恒真的

6.共同蕴含

定理：设G1, …, Gn，H是公式。 称H是G1, …,Gn的逻辑结果(或称G1, …, Gn共同蕴涵H)，当且仅当 (G1$\land$ …\land Gn) \Rightarrow H。 显然，公式H是G1, …, Gn的逻辑结果 iff 公式((G1$\land$ …\land Gn)$\rightarrow$H)是恒真的。

例如，P，P$\rightarrow$Q共同蕴涵Q。

如果H1, …, Hm，P共同蕴涵公式Q，则H1, …, Hm共同蕴涵公式P$\rightarrow$Q。

7.演绎

定理：设S是公式集合，G是一个公式。于是，从S演绎出G的充要条件是G是S的逻辑结果。.

定理： 设S是前提公式集合，G，H是两个公式。 如果从S∪可演绎出H，则从S可演绎出G$\rightarrow$H。

基本蕴含式：

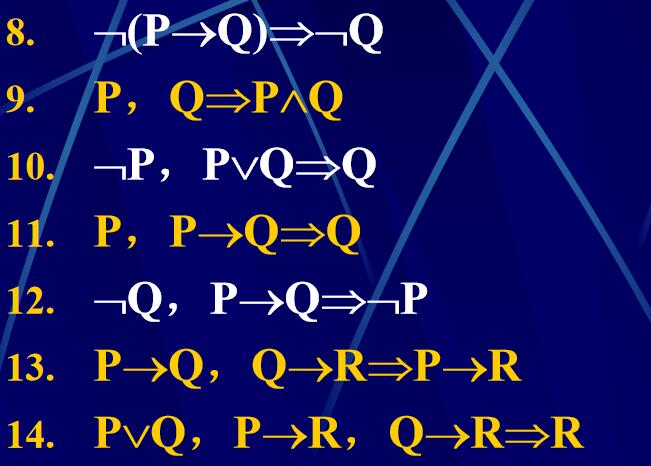
8.公式间蕴涵的证明方法

给出两个公式G，H，证明G蕴涵H。 （1）真值表法； （2）证G$$\rightarrow$$H是恒真公式； （3）利用一些基本等价式及蕴涵式进行推导； （4）任取解释I，若I满足G，往证I满足H； （5）反证法，设结论假，往证前提假 (即证明$\lnot$H \Rightarrow $\lnot$G)

9.形式演绎法

根据一些基本等价式和基本蕴涵式，从S出发，演绎出G，在演绎过程中遵循以下三条规则： 规则1. 可随便使用前提。 (根据演绎定义) 规则2. 可随便使用前面演绎出的某些公 式的逻辑结果。 (根据演绎的定义) 规则3. 如果需要演绎出的公式是P$\rightarrow$Q的形式，可将P做为附加前提使用，而力图去演绎出Q。

范式

1、析取范式和合取范式

原子或原子的否定称为文字(literal)

有限个文字的析取式称为一个子句；

有限个文字的合取式称为一个短语。

特别，一个文字既可称为是一个子句，也可称为是一个短语。

有限个短语的析取式称为析取范式；

有限个子句的合取式称为合取范式。

特别，一个文字既可称为是一个合取范式，也可称为是一个析取范式。一个子句，一个短语既可看做是合取范式，也可看做是析取范式。

定理3.1.4 ：对于任意命题公式，都存在等价于它的析取范式和合取范式。

主析取范式：P、Q.....原始值为1

极小项：对于n个原子P1,…,Pn而言，其不同的解释共有$2n$个，对于P1,…,Pn的任一个极小项m，$2n$个解释中，有且只有一个解释使m取1值。

主析取范式：设命题公式G中所有不同原子为P1,…,Pn，如果G的某个析取范式G’中的每一个短语，都是关于P1,…,Pn的一个极小项，则称G’为G的主析取范式。

定理 ：在真值表中，使得公式为真的解释所对应的极小项的析取即为此公式的主析取范式。

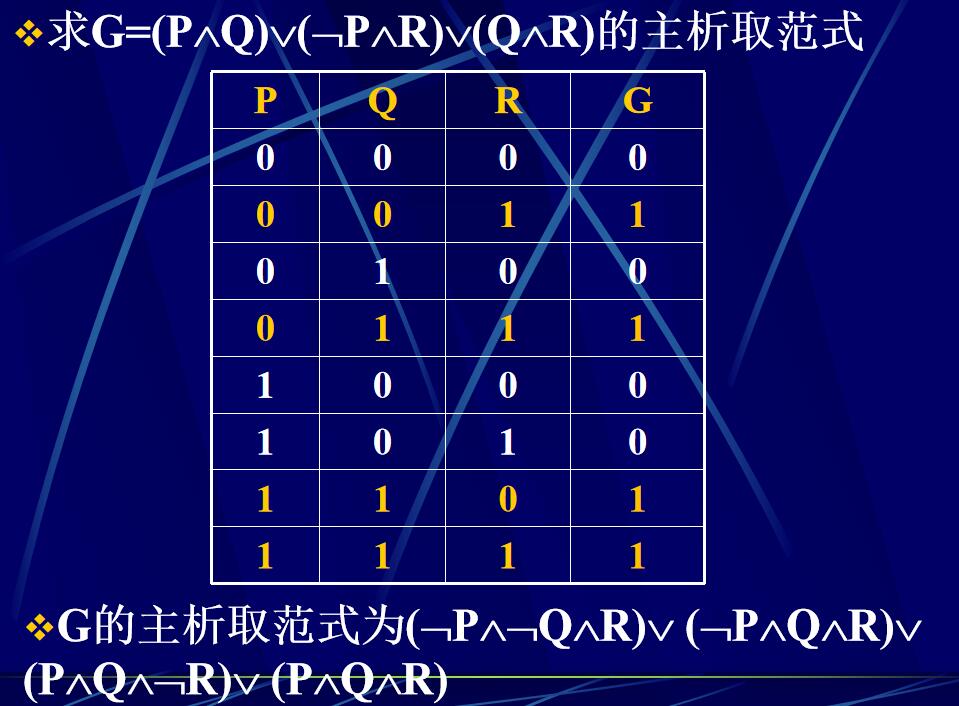
用范式判定公式的恒真恒假性：

引理3.1.2：短语是恒假的当且仅当至少有一个原子及其否定（也称互补对）同时在此短语中出现。

定理3.1.8：命题公式G是恒假的当且仅当在等价于它的析取范式中，每个短语均至少包含一个原子及其否定。

判定公式是否恒真的其它方法：

1.把公式化成主析取范式，公式恒假时，主析取范式没有极小项； 公式恒真时，主析取范式有全部极小项。

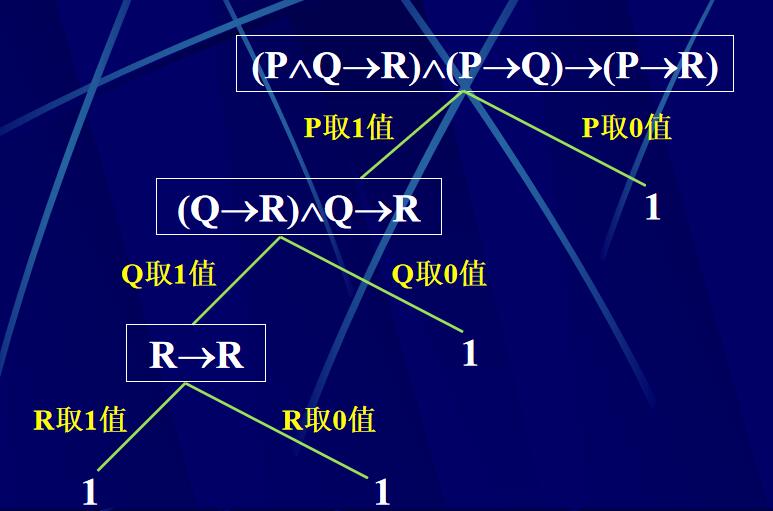
1. 一种判定算法对任给要判定的命题公式G，设其中有原子P1,P2,…,Pn，令P1取1值，求G的真值，或为1，或为0，或成为新公式G1且其中只有原子P2,…, Pn，再令P2取0值，求G真值.如此继续，到最终只含0或1为止，若最终结果全为1，则公式G恒真，若最终结果全为0，则公式G恒假，若最终结果有1，有0，则是可满足的。

主合取范式：P、Q.....原始值为0

极大项

极小项与极大项性质：

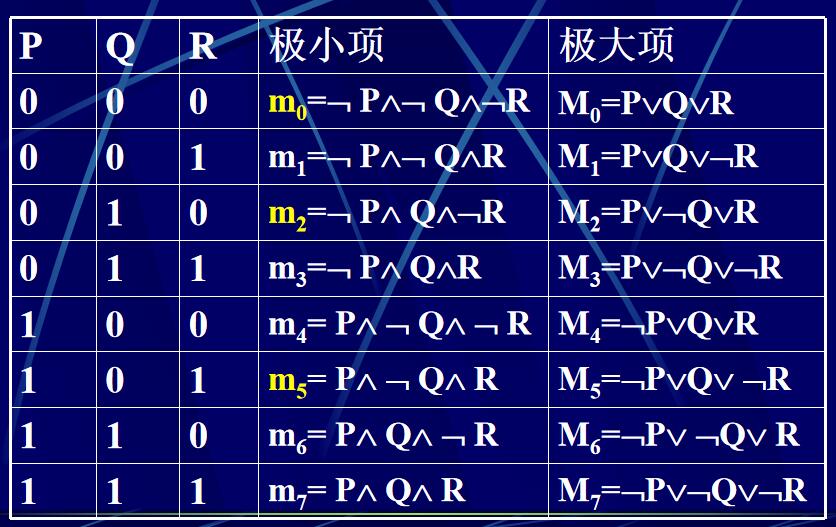
求主合取范式和主析取范式的方法：

方法一. 真值表法。主析取范式恰好是使得公式为真的解释所对应的极小项的析取组成，主合取范式恰好是使得公式为假的解释所对应的极大项的合取组成。

方法二. 公式推导法。

主合取范式与主析取范式的应用：

1.利用主合取范式与主析取范式可求解判定问题

2.证明等价式成立

若二者主范式相同，则给定的两公式是等价的，否则，给定的两公式不等价。

谓词逻辑

谓词逻辑的基本概念

定义3.2.1 ：可以独立存在的物体称为个体。(它可以是抽象的，也可以是具体的。)

定义3.2.2 ：设D是非空个体名称集合，定义在$\mathrm{\mathrm}上取值于{1，0}上的n元函数，称为n元命题函数或n元谓词。其中表\mathrm{\mathrm}$示集合D的n次笛卡尔乘积。

定义3.2.3 ：语句 “对任意x”称为全称量词，记以$\forall x； 语句 “存在一个x”称为存在量词，记以\exists$x。

量词的语义规定：

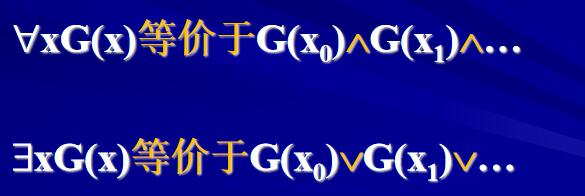
量词的约束范围

定义3.2.4 ：在一个由谓词，量词，逻辑联结词，括号组成的有意义的符号串（实际是指下一节将严格定义的公式）中，称变量的出现是约束的，当且仅当它出现在使用这个变量的量词范围之内；称变量的出现是自由的，当且仅当这个出现不是约束的。

约束变量的改名规则：在由谓词，量词，逻辑联结词，括号组成的有意义的符号串（实际是下节定义的公式）中，可将其中出现的约束变量改为另一个约束变量，这种改名必须在量词作用区域内各处以及该量词符号中实行，并且改成的新约束变量要有别于改名区域中的所有其它变量。 显然改名规则不改变原符号串的真值。

谓词公式

谓词公式的恒真、恒假、可满足

定义3.2.10 ：公式G称为可满足的，如果存在解释I，使G在I下取1值，简称I满足G。若I不满足G，则简称I弄假G。

定义3.2.11 ：公式G称为是恒假的(或不可满足的)，如果不存在解释I满足G；公式G称为恒真的，如果G的所有解释I都满足G。

谓词公式的等价关系和蕴涵关系

公式间的等价：

定义3.2.12 ：公式G，H称为等价，记以G=H，如 果公式G$\leftrightarrow$H是恒真的。 显然，公式G，H等价的充要条件是：对G，H的任意解释I，G，H在I下的真值相同。

公式间的蕴涵：

谓词公式蕴涵的证明方法 ：

范式

前束范式：

定义3.2.14： 谓词逻辑中公式G称为前束范式，如果G有如下形状：Q1x1…QnxnM 其中 Qixi或者是$\forall$xi，或者$\exists$xi，i=1，…，n，M是不含量词的公式，Q1x1…Qnxn称为首标，M称为母式。

对任意谓词公式，量词是不能随便提前的。

引理3.2.1

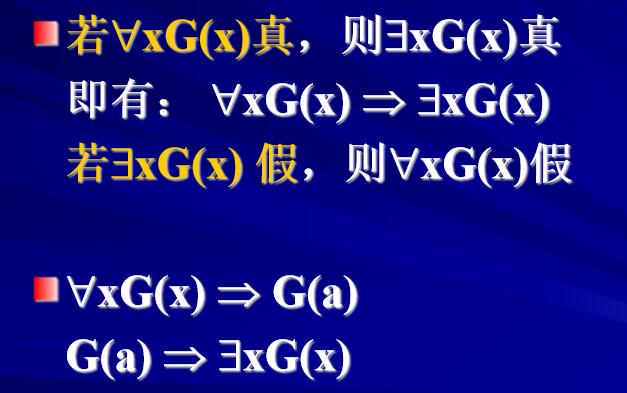
公式的前束范式化：

引理3.2.2 ：

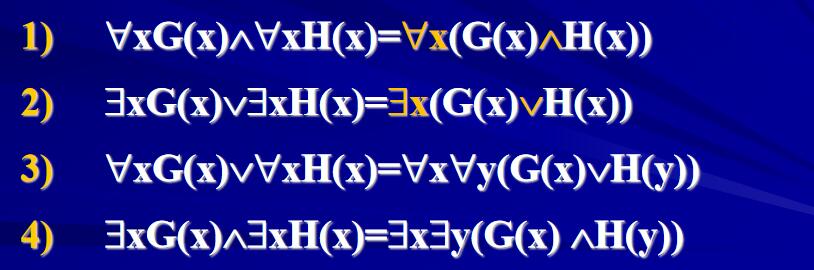
将公式G化成等价的前束范式：

1. 使用基本等价式

​ 2.德摩根率

​ 3.如果必要的话，则将约束变量改名

​ 4.使用引理3.2.1，3.2.2将所有量词都提到公式的最左边。

Skolem范式：

定义3.2.15： 设G是一个公式，Q1x1…QnxnM是与G等价的前束范式，其中M为合取范式形式。 若Qr是存在量词，并且它左边没有全称量词，则取异于出现在M中所有常量符号的常量符号c，并用c代替M中所有的xr，然后在首标中删除Qrxr。若Qs1, …, Qsm是所有出现在Qrxr左边的全称量词(m1,1s1<s2<…<sm<r),则取异于出现在M中所有函数符号的m元函数符号f(xs1,…,xsm )，用f(xs1,…,xsm )代替出现在M中的所有xr，然后在首标中删除Qrxr，对首标中的所有存在量词做上述处理后，得到一个在首标中没有存在量词的前束范式，这个前束范式就称为公式G的Skolem范式。

白话：先把谓词公式化为前束范式，然后看量词符号，存在量词x是标志，用存在量词左边的全称量词作为函数自变量替换范式里的x

注意：

1. Skolem范式与原公式是不等价的
2. 公式G与其Skolem范式S可满足性是等价的
3. G与S的恒假性等价
4. G与S的恒真性不等价
5. S蕴涵G，G不蕴涵S

相关链接

离散数学（集合论） 离散数学（古典数理逻辑） 离散数学（图与网络）