项目实训日志一

项目实训日志一

项目开始已经有几天了，一直在读《Approximation Algorithm》这本书，由于大部分概念都比较陌生，读得很慢，目前主要把第3章的阅读翻译工作完成了。

本章中关键问题是斯坦纳树问题和TSP旅行商问题，在看这两个问题之前要先明确几个概念：
1.最小生成树MST
2.三角不等式
3.欧拉回路
4.哈密顿回路

Chapter3——Steiner Tree and TSP

In this chapter, we will present constant factor algorithms for two fundamental problems, metric Steiner tree and metric TSP. The reasons for considering the metric case of these problems are quite different. For Steiner tree, this is the core of the problem – the rest of the problem reduces to this case. For TSP, without this restriction, the problem admits no approximation factor, assuming P ≠\ne​= NP. The algorithms, and their analyses, are similar in spirit, which is the reason for presenting these problems together.

在本章中，我们将介绍度量斯坦纳树和度量TSP这两个基本问题的常数因子算法。考虑这些问题的度量情况的原因是完全不同的。对于Steiner tree来说，问题的其余部分能够归约化是问题的核心。由于TSP是NP完全问题，因为P≠NP，所以这个问题不可能有多项式时间算法。这两个问题的算法和分析在精神上是相似的，这就是把这两个问题放在一起的原因.

3.1 Metric Steiner tree

度量Steiner tree

The Steiner tree problem was defined by Gauss in a letter he wrote to Schumacher (reproduced on the cover of this book). Today, this problem occupies a central place in the field of approximation algorithms. The problem has a wide range of applications, all the way from finding minimum length interconnection of terminals in VLSI design to constructing phylogeny trees in computational biology. This problem and its generalizations will be studied extensively in this book, see Chapters 22 and 23.
高斯在给舒马赫的一封信中定义了斯坦纳树问题(此书的封面转载)。今天，这个问题占据了近似算法领域的中心位置。该问题具有广泛的应用，从VLSI设计中寻找终端的最小互连长度，到计算生物学中构建系统发育树。这个问题及其概括将在本书第22和23章中被广泛研究。

Problem 3.1 (Steiner tree)

Given an undirected graph G =(V,E) with nonnegative edge costs and whose vertices are partitioned into two sets, required and Steiner, find a minimum cost tree in G that contains all the required vertices and any subset of the Steiner vertices.
We will first show that the core of this problem lies in its restriction to instances in which the edge costs satisfy the triangle inequality, i.e., G is a complete undirected graph,and for any three vertices u, v,and w,cost(u,v)≤ cost(u,w) + cost(v,w). Let us call this restriction the metric Steiner tree problem.
给定一个带权的无向图G =(V,E)，其顶点被划分为required和Steiner两个集合，在G中找到一个包含所有required顶点，和Steiner顶点的任意子集的最小代价树。

[百度：斯坦纳树问题是组合优化问题，与最小生成树相似，是最短网络的一种。最小生成树是在给定的点集和边中寻求最短网络使所有点连通。而最小斯坦纳树允许在给定点外增加额外的点，使生成的最短网络开销最小。最小生成树可以认为是斯坦纳树的特殊情况]

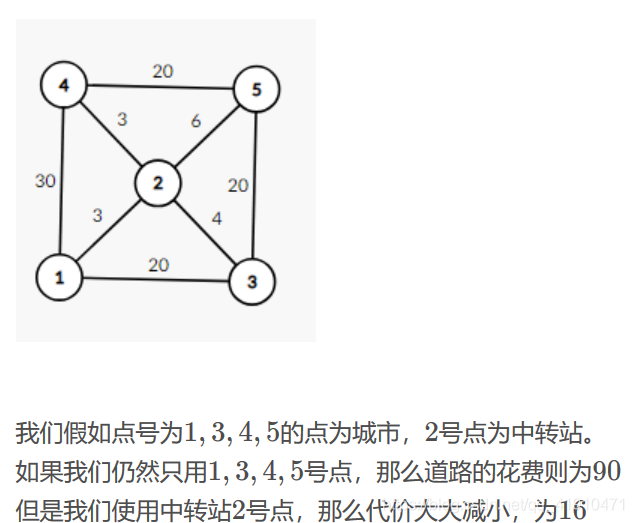
我们要首先说明这个问题的核心在于它对实例的限制，即边代价满足三角形不等式。G是一个完全无向图，对于任意三个顶点u,v,w,cost(u,v)≤cost(u,w) + cost(v,w)。我们把这个限制称为度量斯坦纳树问题。

Theorem 3.2

There is an approximation factor preserving reduction（规约化） from the Steiner tree problem to the metric Steiner tree problem.
从斯坦纳树问题到度量斯坦纳树问题有一个保持近似比的规约化。

[关于规约化]https://baijiahao.baidu.com/s?id=1662884327947972931&wfr=spider&for=pc
归约化是解决复杂问题的一种思路工具，课件中提到了多项式归约，如果我们找到了问题X的多项式时间解法，那么我们有理由相信问题Y同样可以找到多项式时间解法.Y可以在多项式时间内规约为X，这意味着X至少和Y一样困难，因为你如果能解决X，就能解决Y。

Proof: We will transform, in polynomial time, an instance I of the Steiner tree problem, consisting of graph G=(V,E)G =(V,E)G=(V,E), to an instance I′I'I′ of the metric Steiner tree problem as follows. Let G′G'G′ be the complete undirected graph on vertex set V . Define the cost of edge (u,v) in G′G'G′ to be the cost of a shortest u–v path in GGG.G′G'G′ is called the metric closure of G. The partition of V into required and Steiner vertices in I′I'I′ is the same as in III.
证明：我们将在多项式时间内，把由图G=(V,E)组成的斯坦纳树问题的一个实例I变换为度量斯坦纳树问题的一个实例I′I'I′，如下所示。设G′G'G′为顶点集V上的完全无向图。定义G′G'G′中的边(u,v)的代价为GGG中u-v最短路径的代价。G′G'G′被称为GGG的度量闭包。在I′I'I′中将V划分为 required 和 Steiner的方法与III相同。
For any edge (u,v) ∈ E, its cost in G′G'G′ is no more than its cost in G. Therefore, the cost of an optimal solution in I′I'I′ does not exceed the cost of an optimal solution in III.
对于E中的任意边 (u,v)，其在G′G'G′中的代价将不会多于在G中的代价。因此，I′I'I′中一个最优解的代价不会超过III中一个最优解的代价。
Next, given a Steiner tree T′T'T′ in I′I'I′, we will show how to obtain, in polynomial time, a Steiner tree TTT in III of at most the same cost. The cost of an edge (u,v) in G′G'G′ corresponds to the cost of a path in GGG. Replace each edge of T′T'T′ by the corresponding path to obtain a subgraph of GGG. Clearly, in this subgraph, all the required vertices are connected. However, this subgraph may, in general, contain cycles. If so, remove edges to obtain tree TTT. This completes the approximation factor preserving reduction.
接下来，给定I′I'I′中的斯坦纳树T′T'T′，我们将演示如何在多项式时间内获得III中的斯坦纳树TTT，其代价最多相同。G′G'G′ 中一条边(u,v)的代价等于GGG中一条路径的代价。用对应的路径替换T '的每条边，得到GGG的子图。显然，在这个子图中，所有的required顶点都被连接起来了。然而，这个子图通常会包含圈。如果是这种情况，就删除边得到树t，这样完成了近似值保留约简。

下面解释的这部分是同组另一位同学做的：
[这部分我来大概解释一下吧。这里概念确实多而乱，我们捋一捋]

我们举个例子，设图G如下：

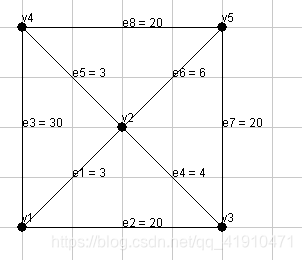
第一个概念是图G=(V,E)的度量闭包G’，这个图G’是一个完全图（其顶点集合和G一样是V，但是边集不一样），G’上的边(u,v)的值被定义为G中u-v的最短路代价。看看下图验证一下G’是不是你理解的样子吧：

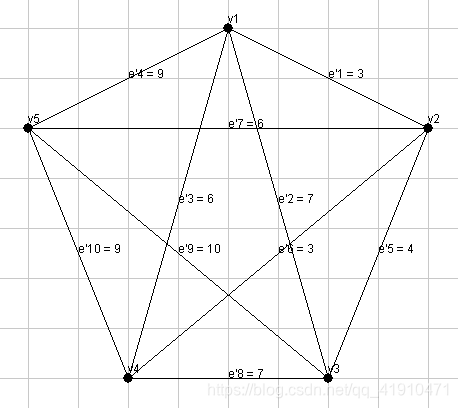
在G’中，每条边都对应了G中的一条最短路，也就是对应了G中一组边的集合：

• e’1 <—> {e1}
• e’2 <—> {e1,e4}
• e’3 <—> {e1,e5}
• …

这里想介绍的思想就是把G上的斯坦纳树问题规约成G’上的斯坦纳树问题（G’上求解的具体做法在下文介绍）当我们求得G’上的生成树，就能按上述对应规则选出G中作为生成树的边。但是直接映射回去可能导致出现环，我们就从环上删除一些边来得到树。

As a consequence of Theorem 3.2, any approximation factor established for the metric Steiner tree problem carries over to the entire Steiner tree problem.

作为定理3.2的结果，为度量斯坦纳树问题所建立的任何近似因子都适用于整个斯坦纳树问题。

3.1.1 MST-based algorithm

[这篇应该是想说我们在G’上用最小生成树作为斯坦纳树的近似]

Let R denote the set of required vertices. Clearly, a minimum spanning tree (MST) on R is a feasible solution for this problem. Since the problem of finding an MST is in P and the metric Steiner tree problem is NP-hard, we cannot expect the MST on R to always give an optimal Steiner tree; below is an example in which the MST is strictly costlier.
设R表示所需顶点的集合。显然，R上的最小生成树(MST)是这个度量斯坦纳树问题的可行解决方案。由于寻找一个MST的问题是在P中，而度量斯坦纳树的问题是np困难的，我们不能期望在R上的MST总是给出一个最优斯坦纳树。

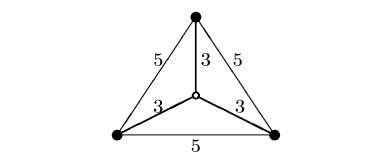
Even so, an MST on R is not much more costly than an optimal Steiner tree:
即使如此，一个在R上的MST并不比一个最优斯坦纳树花费更多:

Theorem 3.3

The cost of an MST on R is within 2·OPT.
在R上的MST的成本是在2OPT以内的。

Proof: Consider a Steiner tree of cost OPT. By doubling its edges we obtain an Eulerian graph connecting all vertices of R and, possibly, some Steiner vertices. Find an Euler tour（欧拉序列） of this graph, for example by traversing the edges in DFS (depth first search) order:
证明:考虑最优代价的斯坦纳树。通过将它的边加倍，我们得到了一个连接R的所有顶点的欧拉图，可能还有一些斯坦纳顶点。查找此图的欧拉序列（回路？），例如以DFS(深度优先搜索)的顺序遍历边:

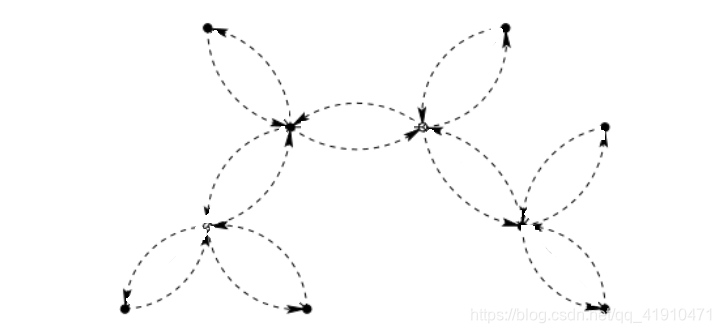
The cost of this Euler tour is 2·OPT. Next obtain a Hamiltonian cycle on the vertices of R by traversing the Euler tour and “short-cutting” Steiner vertices and previously visited vertices of R:
欧拉序列的代价是2OPT。然后通过遍历欧拉序列和“短切”Steiner顶点和R中之前访问过的顶点，得到R顶点上的哈密顿回路:

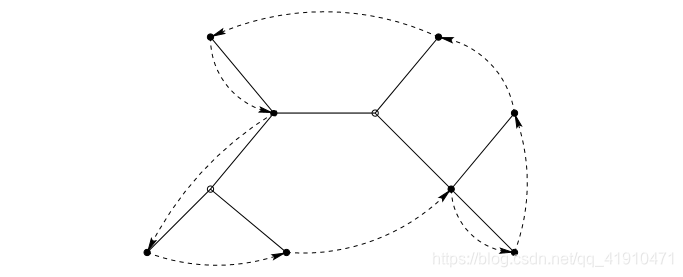
Because of triangle inequality, the shortcuts do not increase the cost of the tour. If we delete one edge of this Hamiltonian cycle, we obtain a path that spans R and has cost at most 2·OPT. This path is also a spanning tree on R. Hence, the MST on R has cost at most 2·OPT.
由于三角不等式，走捷径不会增加成本。如果我们删除这个哈密顿回路的一条边，我们就得到了一条覆盖所有R顶点的路径，其代价最多为2·OPT。此路径也是R上的生成树，因此，R上的MST最多花费2·OPT。
Theorem 3.3 gives a straightforward factor 2 algorithm for the metric Steiner tree problem: simply find an MST on the set of required vertices. As in the case of set cover, the “correct” way of viewing this algorithm is in the setting of LP-duality theory. In Chapters 22 and 23 we will see that LP-duality provides the lower bound on which this algorithm is based and also helps solve generalizations of this problem.
定理3.3为度量斯坦纳树问题提供了一个直接的近似比为2的算法:简单地在所需顶点的集合上找到一个MST。

Example 3.4

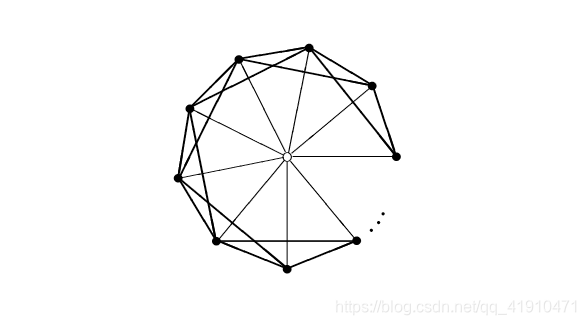
For a tight example, consider a graph with n required vertices and one Steiner vertex. An edge between the Steiner vertex and a required vertex has cost 1, and an edge between two required vertices has cost 2 (not all edges of cost 2 are shown below). In this graph, any MST on R has cost 2(n−1), while OPT = n.
举一个紧密的例子，考虑一个有n个需要顶点和一个斯坦纳顶点的图。斯坦纳顶点和必需顶点之间的一条边的代价为1，两个必需顶点之间的一条边的代价为2(图中没有画出所有代价为2的边)。在这个图中，R上的任何MST代价为2(n−1)，而OPT = n。

3.2 Metric TSP

度量TSP
The following is a well-studied problem in combinatorial optimization.

Problem 3.5 (Traveling salesman problem (TSP)) 旅行商问题

Given a complete graph with nonnegative edge costs, find a minimum cost cycle visiting every vertex exactly once. In its full generality, TSP cannot be approximated, assuming P≠\ne​=NP.
给定一个带权完全图，找到一个每个顶点都经过一次的代价最小的回路。假定P≠\ne​=NP，就其完全的一般性而言，TSP不能近似估计（？）。

Theorem 3.6

For any polynomial time computable function α(n), TSP cannot be approximated within a factor of α(n), unless P = NP.
对于任何多项式时间可计算的函数α(n)，TSP是不能用α(n)的近似比估计的，除非P = NP。
Proof: Assume, for a contradiction, that there is a factor α(n) polynomial time approximation algorithm,A, for the general TSP problem. We will show that A can be used for deciding the Hamiltonian cycle problem (which is NP-hard) in polynomial time, thus implying P = NP.
[反证法]假设存在一个α(n)因子的多项式时间近似算法A，用于一般TSP问题。我们将证明A可以用于在多项式时间内确定哈密顿回路问题(NP-hard)，从而意味着P = NP。
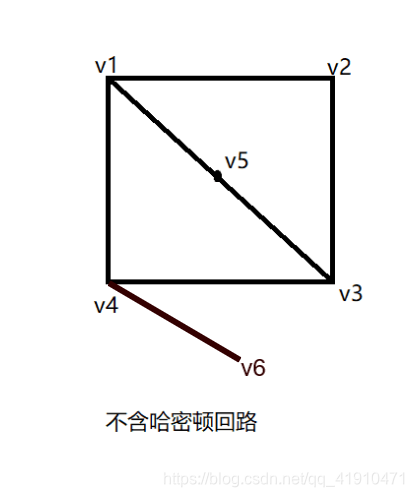
The central idea is a reduction from the Hamiltonian cycle problem to TSP, that transforms a graph G on n vertices to an edge-weighted complete graph G’ on n vertices such that
• if G has a Hamiltonian cycle, then the cost of an optimal TSP tour in G’ is n, and
• if G does not have a Hamiltonian cycle, then an optimal TSP tour in G’ is of cost >α(n)·n.
其核心思想是将哈密顿回路问题归约化为TSP问题，即把具有n个顶点的图G转换为具有n个顶点的带权完全无向图G’。这样的话：
• 如果G中存在哈密顿回路，那么在G’上进行一次最佳TSP旅行的成本是n；
• 如果G中不存在哈密顿回路，那么在G’上进行一次最佳TSP旅行的成本大于α(n)·n；

Observe that when run on graph G’,algorithm A must return a solution of cost ≤ α(n)·n in the first case, and a solution of cost >α (n)·n in the second case. Thus, it can be used for deciding whether G contains a Hamiltonian cycle.
观察到，在图G’上运行时，算法A在第一种情况下一定会返回cost≤ α(n)·n的解，在第二种情况下一定会返回cost >α (n)·n的解。因此，它可以用来确定G是否包含一个哈密顿回路。
The reduction is simple. Assign a weight of 1 to edges of G, and a weight of α(n)· n to nonedges, to obtain G’. Now, if G has a Hamiltonian cycle, then the corresponding tour in G’ has cost n. On the other hand, if G has no Hamiltonian cycle, any tour in G’ must use an edge of cost α(n)·n, and therefore has cost >α (n)·n.
归约化很简单。给G的边赋权值1，给nonedges赋值α(n)· n来得到G’。这样，如果G中有哈密顿回路，那么G’中对应的tour代价为n。另一方面，如果G中没有哈密顿回路，那么G’中的任意tour都必须使用代价为α(n)·n的边，因此就有代价大于α(n)·n。
Notice that in order to obtain such a strong nonapproximability result, we had to assign edge costs that violate triangle inequality. If we restrict ourselves to graphs in which edge costs satisfy triangle inequality, i.e., consider metric TSP, the problem remains NP-complete, but it is no longer hard to approximate.
注意，为了获得如此强不可估计的结果，我们必须分配违反三角形不等式的边代价。如果我们限制边代价满足三角形不等式，也就是考虑度量TSP，问题仍然是NP-complete的，但它不再难以估计。

3.2.1 A simple factor 2 algorithm

We will first present a simple factor 2 algorithm. The lower bound we will use for obtaining this factor is the cost of an MST in G. This is a lower bound because deleting any edge from an optimal solution to TSP gives us a spanning tree of G.
我们首先介绍一个简单的近似比为2的算法。G中一个MST的代价是我们用来获得这个近似比的下界。它之所以是一个下界，是因为从TSP的最优解中删除任何一条边都会给我们一个G的生成树。

Algorithm 3.7 (Metric TSP – factor 2)

1.Find an MST,T, ofG.
2.Double every edge of the MST to obtain an Eulerian graph.
3.Find an Eulerian tour,τ\tauτ, on this graph.
4.Output the tour that visits vertices of G in the order of their first appearance in τ\tauτ. Let C be this tour.
Notice that Step 4 is similar to the “short-cutting” step in Theorem 3.3.
1.找到G的一个MST，命名为T。
2.将MST的每条边加倍得到欧拉图。
3.在图中找到一个欧拉序列τ\tauτ。
4.按照顶点在τ\tauτ中第一次出现的顺序,输出访问G顶点的序列。这个序列叫C。
注意，步骤4类似于定理3.3中的“捷径”步骤。

Theorem 3.8

Algorithm 3.7 is a factor 2 approximation algorithm for metric TSP.
算法3.7是度量TSP的近似比为2的近似算法。
Proof: As noted above, cost(T) ≤ OPT. Since τ\tauτ contains each edge of T twice, cost(τ\tauτ)=2·cost(T). Because of triangle inequality, after the “shortcutting” step, cost( C ) ≤ cost(τ\tauτ). Combining these inequalities we get that cost( C )≤2·OPT.
证明：正如上面提到的（下界），cost(T) ≤ OPT。因为τ\tauτ包含T的每条边两次,所以cost(τ\tauτ)=2·cost(T)。由于三角不等式，在“捷径”的那一步之后，cost( C ) ≤ cost(τ\tauτ)。
综上述不等式，可以得到cost( C )≤2·OPT。

Example 3.9

A tight example for this algorithm is given by a complete graph on n vertices with edges of cost 1 and 2. We present the graph for n = 6 below, where thick edges have cost 1 and remaining edges have cost 2. For arbitrary n the graph has 2n−2 edges of cost 1, with these edges forming the union of a star and an n−1 cycle; all remaining edges have cost 2. The optimal TSP tour has cost n, as shown below for n = 6:
该算法的一个紧密例子是一个包含n个顶点、边的代价为1和2的完全图。下面我们给出n = 6的图，其中加粗的边代价为1，其余边代价为2。对于任意n，图有2n - 2条代价为1的边，这些边形成了一个星和一个n - 1回路的并集;所有剩余边的代价都是2。当n = 6时，最优TSPtour的代价为n:

Suppose that the MST found by the algorithm is the spanning star created by edges of cost 1. Moreover, suppose that the Euler tour constructed in Step 3 visits vertices in order shown below for n = 6:
假设该算法找到的MST是代价为1的边生成的生成星。假设在n = 6时，第3步构建的欧拉序列按如下顺序访问顶点:


那么经过shortcut得到的tour包含代价为2的n - 2条边，总代价为2n - 2。渐近地说，这是最优TSP行程的两倍代价。

3.2.2 Improving the factor to 3/2

把近似因子优化至3/2
Algorithm 3.7 first finds a low cost Euler tour spanning the vertices of G, and then short-cuts this tour to find a traveling salesman tour. Is there a cheaper Euler tour than that found by doubling an MST? Recall that a graph has an Euler tour iff all its vertices have even degrees. Thus, we only need to be concerned about the vertices of odd degree in the MST. Let V’ denote this set of vertices.|V’|must be even since the sum of degrees of all vertices in the MST is even. Now, if we add to the MST a minimum cost perfect matching on V’, every vertex will have an even degree, and we get an Eulerian graph. With this modification, the algorithm achieves an approximation guarantee of 3/2.
算法3.7首先找到一个横跨G的顶点的低成本欧拉序列，然后缩短这个路线以找到一个旅行商路线。有比MST翻倍成本更低的欧拉序列吗?回想一下，如果一个图的所有顶点度数都是偶数，那么它就有一个欧拉序列。因此，我们只需要关心MST中奇数度数的顶点。设V ‘表示顶点的集合。|V’|一定是偶数，因为MST中所有顶点的度和是偶数。现在，如果我们在MST中加入V’上的最小代价完美匹配，每个顶点都会是偶数度数的，我们就得到了一个欧拉图。经过这样的修改，算法得到了3/2的近似比。

Algorithm 3.10 (Metric TSP – factor 3/2)

1.Find an MST of G, say T.
2.Compute a minimum cost perfect matching, M, on the set of odd-degree vertices of T. Add M to T and obtain an Eulerian graph.
3.Find an Euler tour,τ\tauτ, of this graph.
4.Output the tour that visits vertices of G in order of their first appearance in τ\tauτ. Let C be this tour.
Interestingly, the proof of this algorithm is based on a second lower bound on OPT.
1.找到G上的一个MST，命名为T。
2.计算T的奇数度数的顶点集合上的最小代价完美匹配M，将M加到T上，得到一个欧拉图。
3.找到这个图的一个欧拉回路τ\tauτ。
4.按照顶点在τ中第一次出现的顺序,输出访问G顶点的序列。这个序列叫C。
有趣的是，这个算法的证明正是基于最优算法的第二个下界（？）。

Lemma 3.11

Let V’⊆ V , such that |V’| is even, and let M be a minimum cost perfect matching on V’. Then, cost(M)≤OPT/2.
令V’⊆V，使（？）|V’|为偶数，设M为V’上的最小代价完美匹配。此时,cost(M)≤OPT / 2。
Proof: Consider an optimal TSP tour of G, say τ\tauτ. Let τ′\tau'τ′ be the tour on V’ obtained by short-cutting τ\tauτ. By the triangle inequality, cost(τ′\tau'τ′) ≤cost(τ\tauτ). Now, τ′\tau'τ′ is the union of two perfect matchings on V’, each consisting of alternate edges of τ\tauτ. Thus, the cheaper of these matchings has cost ≤ cost(τ′\tau'τ′)/2 ≤ OPT/2. Hence the optimal matching also has cost at most OPT/2.
证明：考虑G上的一个最优TSP序列，如τ\tauτ。设τ′\tau'τ′是通过short-cutτ\tauτ得到的在V’上的序列。由三角不等式可知，cost(τ′\tau'τ′) ≤cost(τ\tauτ)。现在，τ′\tau'τ′是V’上的两个完美匹配的并集，这两个匹配的每条边都由τ\tauτ的交替边（？）组成。因此，这些匹配中较低的cost≤cost(τ′\tau'τ′)/2≤OPT/2。因此，最优匹配的代价也最多为OPT/2。

Theorem 3.12

Algorithm 3.10 achieves an approximation guarantee of 3/2 for metric TSP.
算法3.10达到了度量TSP的3/2的近似比。
Proof: The cost of the Euler tour,
cost(τ\tauτ)≤cost(T)+cost(M)≤OPT+1/2OPT=3/2OPT,
where the first inequality follows by using the two lower bounds on OPT. Using the triangle inequality, cost( C )≤cost(τ\tauτ), and the theorem follows.
证明：欧拉序列的代价
cost(τ\tauτ)≤cost(T)+cost(M)≤OPT+1/2OPT=3/2OPT,
其中第一个不等式使用在最优算法上的两个下界。而由三角不等式，cost( C )≤cost(τ\tauτ)，得上式。

Example 3.13

A tight example for this algorithm is given by the following graph on n vertices, with n odd:
下面给出一个关于此算法的例子n个顶点的图，其中n为奇数:

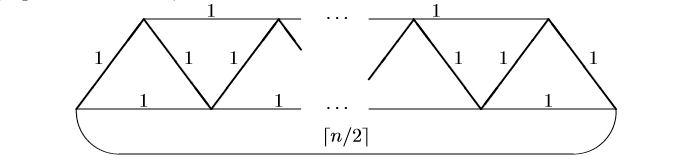
Thick edges represent the MST found in step 1. This MST has only two odd vertices, and by adding the edge joining them we obtain a traveling salesman tour of cost (n−1)+⌈\lceil⌈n/2⌉\rceil⌉. In contrast, the optimal tour has cost n.
粗边表示步骤1中找到的MST。这个MST只有两个奇数度的顶点，并且通过添加连接这些顶点的边，我们得到一个代价为(n−1)+⌈\lceil⌈n/2⌉\rceil⌉的旅行商序列。相比之下，最优序列的代价是n。
Finding a better approximation algorithm for metric TSP is currently one of the outstanding open problems in this area. Many researchers have conjectured that an approximation factor of 4/3 may be achievable.
寻找一种更好的度量TSP近似算法是目前该领域一个悬而未决的问题。许多研究者推测4/3的近似比是可以实现的。

另外，同组的另外一位同学也对斯坦纳树的关键问题做了一点总结:
添加链接描述