测试开发基础之算法(12):支持动态数据集合快速插入、删除、查找的二叉查找树

上一篇文章，学习了二叉树的前序、中序、后序和按层遍历方法，以及如何求二叉树的最大最小深度。
今天我们再来看一种更加特殊二叉树——二叉查找树。二叉查找树最大的特点是，支持动态数据集合的快速插入、删除、查找操作。
不过，你应该还记得，之前介绍的线性数据结构散列表，也支持数据的快速插入、删除、查找操作，而且时间复杂度是 O(1)。二叉查找树还能比这个时间复杂厉害？带着这个问题，我们开始学习二叉查找树。

1. 二叉查找树

二叉查找树的特点是，当前节点的值，大于它左子树中所有节点的值，而小于它右子树中所有节点的值。举几个例子看看：

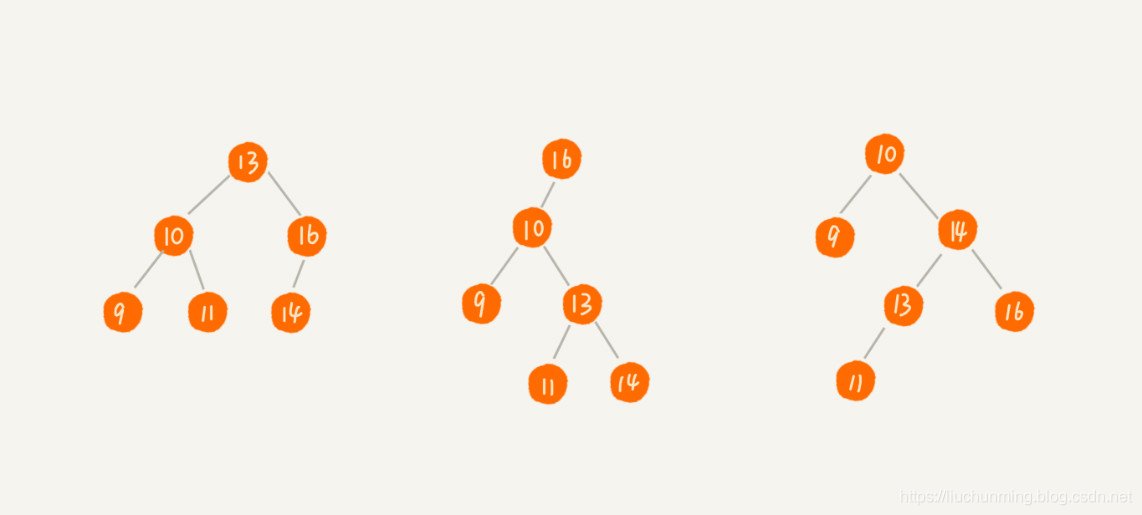
2.查找数据

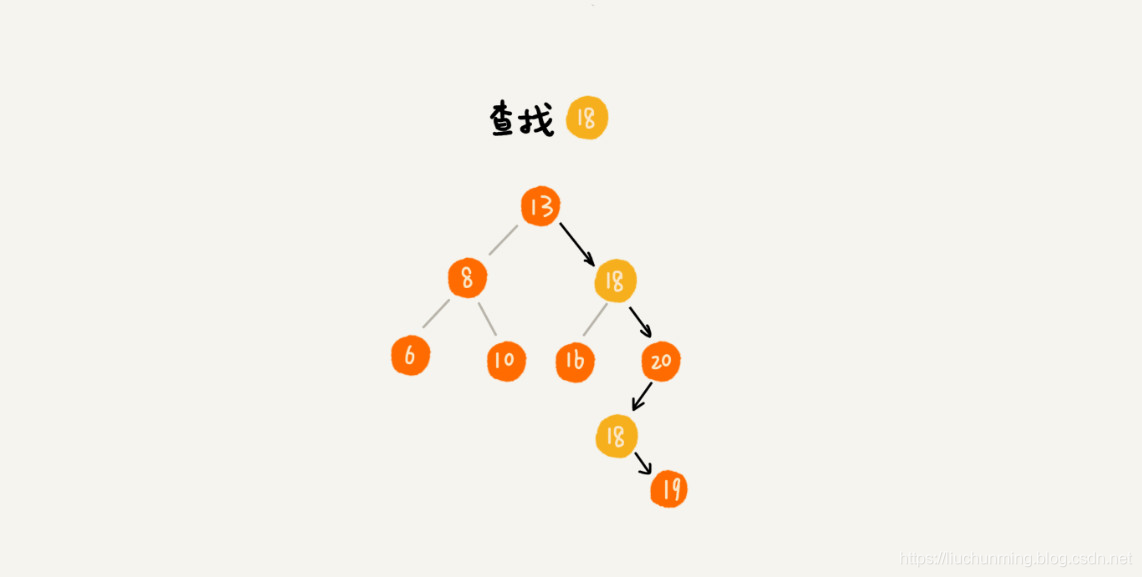
利用二叉查找树的特点，当前结点node大于左子树node.left的所有节点，小于右子树node.right的所有节点。因此，查找值为data 的节点时，当data<node时，则要在左子树中继续查找，如果data>node时，则要在右子树中继续查找，直到查找的节点为None，表示没有找到。用代码表示：

from typing import TypeVar, Generic, Optional

T = TypeVar("T")

class TreeNode(Generic[T]):
def __init__(self, value):
self.value = value
self.left = None
self.right = None

def search(node: Optional[TreeNode], data: Generic[T]) -> Optional[TreeNode]:
while node:
if data < node.value:  # 在左子树中找
node = node.left
elif data > node.value: # 在右子树中找
node = node.right
else:  # 找到了
return node
return None

if __name__ == '__main__':
root = TreeNode(16)  # 构造一个二叉查找树，样子就是第一节中间那个图
first = TreeNode(10)
second = TreeNode(9)
third = TreeNode(13)
fourth = TreeNode(11)
fifth = TreeNode(14)
root.left = first
first.left = second
first.right = third
third.left = fourth
third.right = fifth

print(search(root, 13))

3.插入数据

插入的操作跟查找数据类似。先插入的节点一般会插在叶子节点，也是从根节点开始，逐个比较节点与插入的数据大小。
当二叉查找树的根节点为空时，将数据直接放到根节点就行了。
如果插入的数据比当前节点大，看看这个节点的右子树是否为空，如果是空，直接将数据放到右子节点上。如果不空，则在右子树上继续找插入的位置。
如果插入的数据比当前节点小，看看这个节点的左子树是否为空，如果为空，直接将数据放到左子节点上。如果不空，则在左子树上继续找插入的位置。
代码如下：

def insert(node: Optional[TreeNode], data: Generic[T]):
if node is None:
node = TreeNode(data)
return None
while node:
if data < node.value:
if node.right is None:
node.right = TreeNode(data)
return None
node = node.right
else:
if node.left is None:
node.left = TreeNode(data)
return None
node = node.left

4.删除数据

给定一个二叉搜索树的根节点 node 和一个值value ，删除二叉搜索树中的 value 对应的节点，并保证删除后依然是二叉查找树。

相比查找和插入，删除操作有点复杂。需要考虑三种情况。

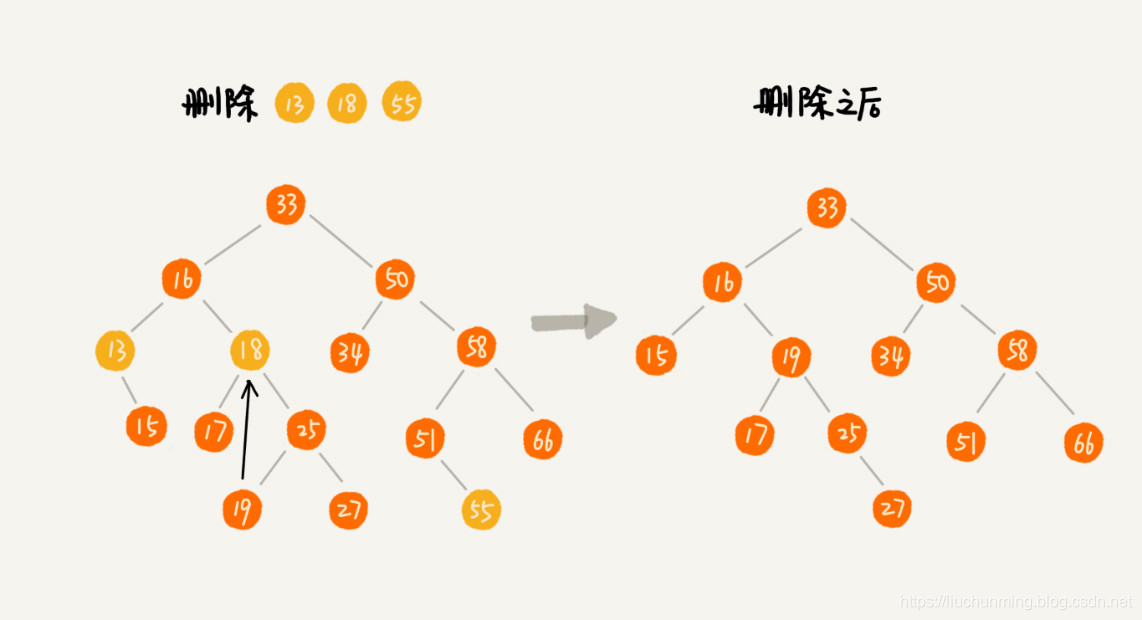
我们以删除上面树中55，13，18，三个被删除节点为例，说明一下删除的思路和过程。

• 55这个节点，没有左子节点，也没有右子节点。删除55这个节点，只需要将他的父节点指向None就行了。
• 13这个节点，只有一个子节点，没有左子节点，只有右子节点。删除13这个节点，将它父节点指向它的指针，指向它的右子节点。
• 18这个节点，有两个子节点，用它的右子树中的最小节点替换它，然后再删除右子树中的最小节点（最小节点肯定没有左子节点如果有左子结点，那就不是最小节点了）。如何删除右子树的最小节点呢？参考删除55和13这两个节点的方法。

可见整个删除过程中，查找被删除节点和它的父节点是关键。

下面看看代码实现：

def remove(node: Optional[TreeNode], data: Generic[T]) -> Optional[TreeNode]:
pp = None
while node and node.value != data:
pp = node  # 被删除节点的父节点
node = node.left if node.value > data else node.right  # node是被删除节点

if node is None:  # 没找到
return None

# 被删除的节点有两个子节点
if node.left and node.right:  # 寻找右子树的最小节点（这个节点肯定没有左子节点，要么是叶子节点要么只有一个右子节点）
min_p = node.right  # 最小节点，初始化为被删除节点的右节点
min_pp = node  # 最小节点的父节点，初始化为被删除节点
while min_p.left:  # 最小节点肯定在被删除节点的右子树的左子树中
min_p = min_p.left
min_pp = min_p
node.value = min_p.value  # 最小节点的值放到node上
# 这两句话就是把问题转化为删除最小节点min_p的问题了（画下图就能明白了）
pp = min_pp
node = min_p

# 删除的节点是叶子节点或者仅有一个子节点（如果上面的if成立，这里的node就是min_p了）
if node.left:  # 当有一个左子节点，找到它的子节点child
child = node.left
elif node.right:  # 当有一个右子节点，找到它的子节点child
child = node.right
else:  # node是叶子节点，它的子节点就是None
child = None
if pp is None: # 删除的是根节点
node = child
elif pp.left == node:
pp.left = child
else:
pp.right = child

if __name__ == '__main__':
root = TreeNode(16)
first = TreeNode(10)
second = TreeNode(9)
third = TreeNode(13)
fourth = TreeNode(11)
fifth = TreeNode(14)
seven = TreeNode(18)
root.left = first
root.right = seven
first.left = second
first.right = third
third.left = fourth
third.right = fifth

remove(root, 16)
print(list(in_order(root)))

参考https://leetcode-cn.com/problems/delete-node-in-a-bst/solution/python3cai-yong-suan-fa-4ti-gong-de-si-lu-bu-zou-q/的解答。

5. 查找最大最小节点

二叉查找树的最大节点是在右子树中没有右子节点的那个结点。最小节点是左子树中没有左子节点的那个结点。

思路很清晰了，既可以用递归实现也可以循环实现。

对于递归查找最小节点，一开始先判断节点是否为空，如果为空就返回None，否则一直往左递归，直到找到最左节点，则是最小节点。
对于递归查找最大节点，一开始先判断节点是否为空，如果为空就返回None，否则一直往右递归，直到找到最右节点，则是最大节点。

迭代方法查找也是，一开始判断结点空不空，不空就进入while循环。对于查找最小值，只要节点的左子树不为None，就让node=node.left，直到node.left为None了，就证明找到了最左的节点，此时退出了while循环，return node。
查找最大节点方法一样，循环右子树直到找到最右结点，再return出去就可以了。

def min_node(node: Optional[TreeNode[T]]) -> Optional[TreeNode]:
if node is None:
return None
# while node.left:
#     node = node.left
# return node
elif node.left is None:
return node
else:
return min_node(node.left)

def max_node(node: Optional[TreeNode[T]]) -> Optional[TreeNode]:
if node is None:
return None
# while node.right:
#     node = node.right
# return node
elif node.right is None:
return node
else:
return max_node(node.right)

6.查找前驱节点和后继节点

前驱节点(predecessor)指的是比给定节点value值小的所有节点中最大的节点。后继节点（successor）指的是比给定结点value值大的所有节点中最小的节点。
换个说法，前驱节点就是给定节点左子树中最右边节点(right most node)，后继节点就是给定节点右子树中最左边的节点(left most node)。举例，下图6的前驱节点是左子树的最右边节点(right most node)5，后继节点是右子树的最左边节点(left most node)7。

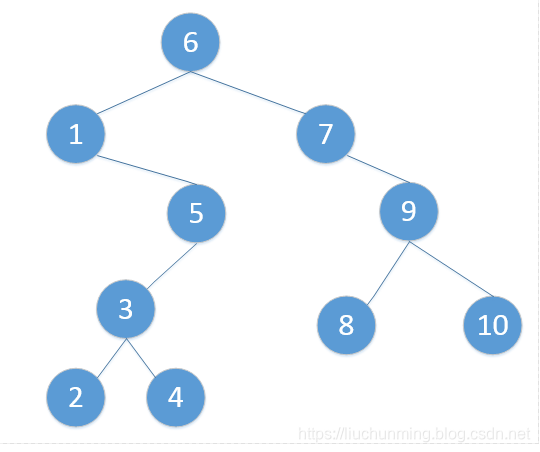
从上面的图中，可以得出：

• 6的前驱结点是5，后继节点是7
• 2的前驱节点是1，后继节点是3
• 4的前驱节点是3，后继节点是5

根据上述例子，我们可以得到下述规则：

• 前驱节点

1. 若一个节点有左子树，那么该节点的前驱节点是其左子树中value值最大的节点。
2. 若一个节点没有左子树，那么判断该节点和其父节点的关系。
   2.1 若该节点是其父节点的右节点，它的父节点就是它的前驱节点。
   2.2 若该节点是其父节点的左节点，那么沿着其父亲节点往根节点找，直到找到一个节点p，p节点是p的父节点pp的右节点（可参考例子2的前驱节点是1），那么pp就是该节点的前驱节点。

类似，可以得到求后继节点的规则如下。

• 后继节点

1. 若一个节点有右子节点，那么该节点的后继节点是其右子树中value值最小的节点。
2. 若一个节点没有右子节点，那么判断该节点和其父节点的关系。
   2.1 若该节点是其父节点的左子节点，那么该节点的父节点就是后继节点。
   2.2 若该节点是其父节点的右子节点，那么沿着其父亲节点往根节点找，直到找到一个节点p，p节点是其父节点pp的左子节点（可参考例子5的后继结点是6），那么pp就是该节点的后继节点。

当然我们可以对一个二叉搜索树直接进行中序遍历，立马可以得到节点的前驱和后继节点，但是这样的方法时间复杂度为O(N)，显然不是最好的方法。而上面算法的时间复杂度是O(logN)。

前面的规则，我们是从下往上来寻找前驱节点和后继节点的。但是在编码时，我们没有办法从下往上，只能从上往下查找，在查找过程中记录父节点。

有了上面的规则，我们用代码来实现一下。

def inorder_successor(root: Optional[TreeNode[T]], value) -> Optional[TreeNode[T]]:
"""
后继节点（successor）指的是比给定结点value值大的所有节点中最小的节点。换个说法，后继节点就是给定节点右子树中最左边的节点(left most node)
算法思路：从根节点开始逐个与给定节点对比。见下面注释。
:param root: 当前节点
:param value: 给定结点的值
:return: 后继节点
"""
# 方法一：通过递归
# if root:
#     if root.value > value:  # value在root的左子树中
#         return inorder_successor(root.left, value) or root
#     return inorder_successor(root.right, value)

# 方法二：通过迭代
res = None  # 后继节点res，初始化为None
while root:  # 当前节点初始化为root，随着迭代的进行，root在变
if root.value > value:  # 当前节点值比给定节点的值大
res = root  # 当前结点作为后继节点，但不一定哦
root = root.left  # 到左子树中继续找是否也有比给定值大的节点，如果有更新res，如果没有左子树，while循环结束，返回res。
else:  # 当前节点的值比给定节点小
root = root.right  # 在到右子树找
return res  # 返回后继节点

def inorder_predecessor(root: Optional[TreeNode[T]], value) -> Optional[TreeNode[T]]:
"""
前驱节点（predecessor）指的是比给定结点value值小的所有节点中最大的节点。换个说法，前驱节点就是给定节点左子树中最右边的节点(right most node)
算法思路：从根节点开始逐个与给定节点对比。见下面注释。
:param root: 当前节点
:param value: 给定结点的值
:return: 前驱节点
"""
# 方法一：通过递归
# if root:
#     if root.value < value:  # 当前节点值小于给定节点
#         return inorder_predecessor(root.right, value) or root
#     return inorder_predecessor(root.left, value)

# 方法二：通过迭代
res = None  # 前驱节点res，初始化为None
while root:  # 当前节点初始化为root，随着迭代的进行，root在变
if root.value < value:  # 当前节点值比给定节点的值小
res = root  # 当前结点作为前驱节点，但不一定是真正的前驱节点
root = root.right  # 到右子树中继续找是否也有比给定值小的节点，如果有更新res，如果没有右子树，while循环结束，返回res。
else:
root = root.left  # 在到左子树找
return res  # 返回前驱节点

二叉查找树除了支持上面几个操作之外，还有一个重要的特性，就是中序遍历二叉查找树，可以输出有序的数据序列，时间复杂度是 O(n)，非常高效。因此，二叉查找树也叫作二叉排序树。

7.二叉查找树的时间复杂度分析

下面是三中二叉查找输的例子，从平衡性角度，他们的结构差别比较大。最左边的极度不平衡，已经从二叉树退化成链表了。最右边的是完全二叉树，是高度平衡的。不管操作是插入、删除还是查找，时间复杂度其实都跟树的高度成正比，也就是 O(height)。而height最大值是N，最小值是log2N。因此二叉查找树的时间复杂度，介于O(N)和O(log2N)。

8.二叉查找树与散列表的比较

散列表的插入、删除、查找操作的时间复杂度可以做到常量级的 O(1)，非常高效。而二叉查找树在比较平衡的情况下，插入、删除、查找操作时间复杂度才是 O(logn)，相对散列表，好像并没有什么优势，那我们为什么还要用二叉查找树呢？

主要原因应该有以下几点：

第一，散列表中的数据是无序存储的，如果要输出有序的数据，需要先进行排序。而二叉查找树中序遍历，就可以在O(n)的时间复杂度内输出有序序列。

第二，散列表扩容比较耗时，遇到散列冲突时，性能衰减太快。尽管二叉查找树的性能也不稳定，但是工程实际应用中的平衡二叉查找树的性能非常稳定，是O(logN)。

第三，散列表的构造比较复杂，需要考虑哈希算法设计、散列冲突、扩容、缩容等，而二叉查找树的构造，只需要考虑平衡性。

第四，尽快散列表的时间复杂度是常量级O(1)，但是遇到散列冲突时，这个常量不一定比二叉查找树的logN小。加上哈希函数的耗时，总的效率不一定比平衡二叉查找树高。

9. 求N个节点的完全二叉树的高度

可以参考https://liuchunming.blog.csdn.net/article/details/103420491这篇文章中，求二叉树最大最小深度的练习题。

11.重复数据的二叉查找树

前面介绍的二叉查找树是不包含重复数据的情况。当有重复数据时，查找、插入和删除高如何操作呢？

在查找插入位置的过程中，如果碰到一个节点的值，与要插入数据的值相同，我们就将这个要插入的数据放到这个节点的右子树，也就是说，把这个新插入的数据当作大于这个节点的值来处理。

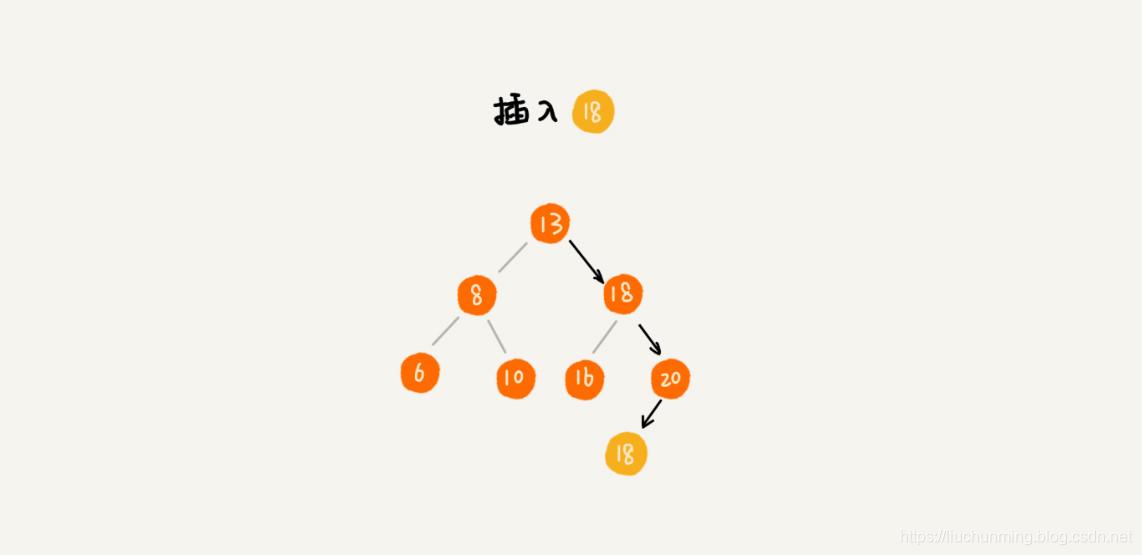
当要查找数据的时候，遇到值相同的节点，我们并不停止查找操作，而是继续在右子树中查找，直到遇到叶子节点，才停止。这样就可以把键值等于要查找值的所有节点都找出来。

对于删除操作，我们也需要先查找到每个要删除的节点，然后再按前面讲的删除操作的方法，依次删除。