二分搜索树看这篇就足够了

二分搜索树(BST):中序遍历结果为递增序列

BST是一种特殊的二叉树，其定义如下：

BST ：在二叉树的基础上，任意一个节点满足大于左子树中的所有节点，小于右子树中的所有节点。

注意点：

• BST的定义中没有等号，后续代码中可以看到，在插入时，相等的元素会被忽略掉。
• BST的中序遍历结果为递增序列(应用很广)，证明：L<node<R;
• BST是动态数据结构，即容量会自动扩缩(插入，删除)。

插入过程:牢记BST的定义,为null时才插入。

private Node add(Node node,E e)

：向以

node

为根节点的BST中插入新的元素

e

,并返回新的根节点。

private Node add(Node node,E e){
if(node==null){
return new Node(e);
}
if(e.compareTo(node.e)<0){//左边插入。其余不变
node.left=add(node.left,e);
}else if(e.compareTo(node.e)){
node.right=add(node.right,e);
}
//相等，忽略。
return node;
}
public void add(E e){//从根节点开始找。

root=add(root,e);
}

删除过程(最复杂)：牢记BST的定义，找到时才删除。

1. BST的最小值：左子树的终点，不一定是叶子节点。
2. BST的最大值：右子树的终点，不一定是叶子节点。

删除最小或者最大节点

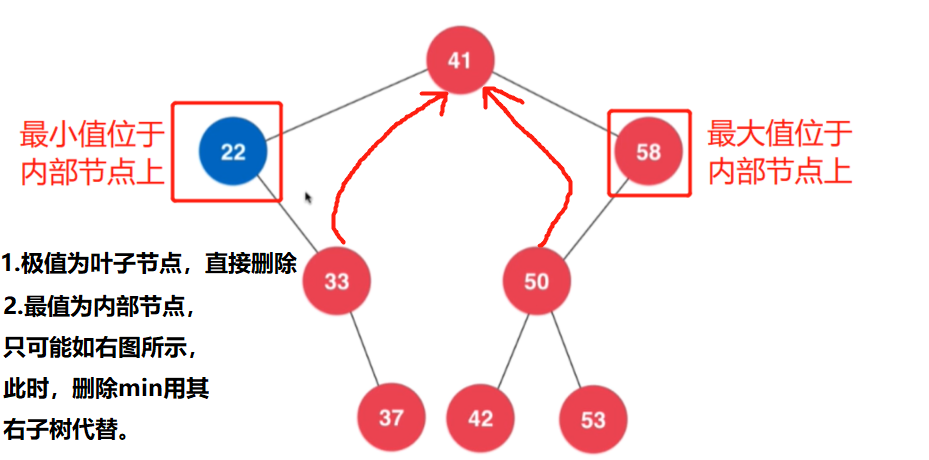
最小值位于节点内部时，其后是一个右子树，此时删除节点后，将剩余子树接到删除节点父节点位置，作为他的左子树。(删除最大值同理)--满足BST性质。

private Node removeMin(Node node)

删除已node为根节点的BST的最小节点，并返回删除节点后新的BST的根节点。

public E removeMin(){
E min=getMin();
root=removeMin(root);
return min;
}
private Node removeMin(Node node){
//found it,左子树的终点
if(node.left==null){
Node rightNode=node.right;
size--;
return rightNode;
}
node.left=removeMin(node.left);
return node;
}

删除任意元素

• 删除的节点只有右孩子 :删除当前节点，然后把右子树放置到当前节点的位置，相当于delMin

• 删除节点只有左孩子：删除当前节点，然后把左子树放置到当前节点的位置，相等于deMax

• 待删除元素左右孩子都有：找到比待删除节点大的最小节点(BST性质)，用这个节点顶替代删除节点的位置。

  

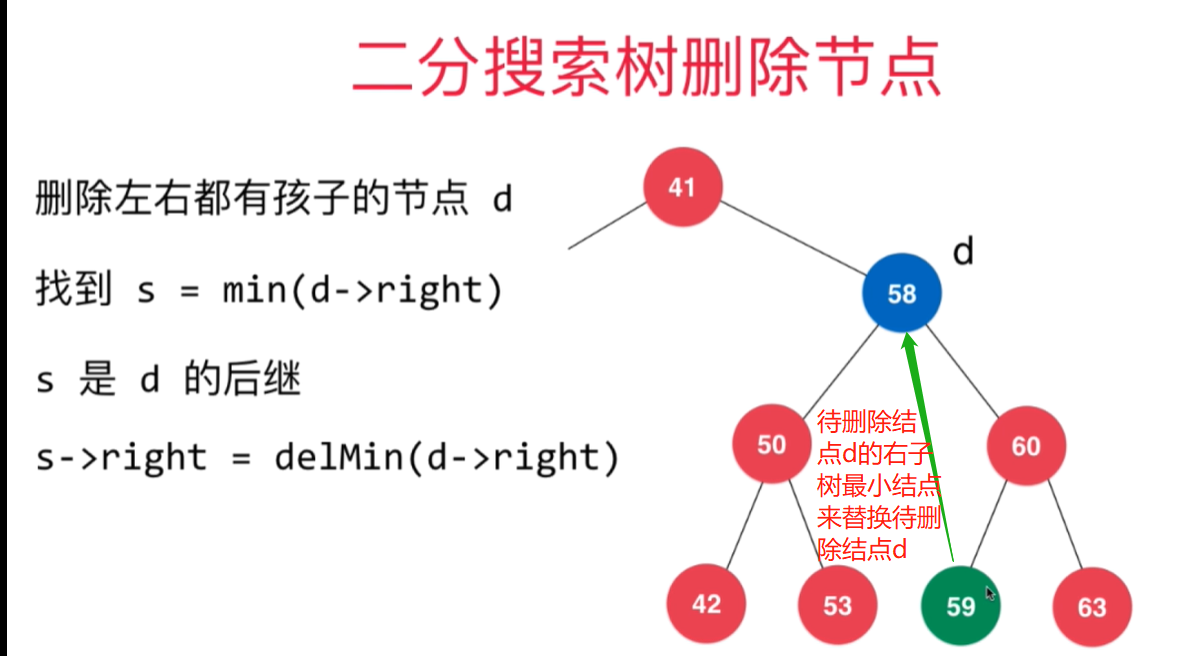
//删除已node为根的BST中值为e的节点，并返回删除之后新的BST的根。
private Node remove(Node node,E e){
if(node==null)return null;
if(e.comapreTo(node.e)<0){
node.left=remove(node.left,e);
return node;
}
else if(e.compareTo(node.e)>0){
node.right=remove(node.right,e);
return node;
}
//找到待删除元素(e.compareTo(node.e)==0)，体会函数执行到这儿的含义。
else{
//待删除节点左子树为null
if(node.left==null){
Node rightNode=node.right;
node.right=null;
size--;
return rightNode;
}
if(node.right==null){
Node leftNode=node.left;
node.left=null;
size--;
return leftNode;
}
//两边都不为null。
Node successor=minimum(node.right);
sussessor.right=removeMin(node.right);//右边最小的。
sussessor.left=node.right;
return sussessor;

}

}

public void remove(E e) {
root = remove(root, e);
}

查找元素：BST性质

private boolean contains(Node node,E e){
if(node==null) return false;
if(e.compareTo(node.e)<0){
return contains(node.left,e);
}else if(e.compareTo(node.e)>0){
return contains(node.right,e);
}else{//先找到，这点和删除的逻辑很像
return true;
}
}
public boolean contains(E e){
return contains(root,e);
}

BST的完整源码请点击这儿

BST缺点：

• 当插入元素有序时，BST退化为单链表。

AVL树：有序性+平衡性

AVL树在BST的基础上增加了平衡性约束。新增的操作(旋转与高度更新)都是为了满足平衡性约束

AVL树中平衡性的定义：

对于任意一个节点，左子树与右子树的高度差不能超过1

平衡二叉树中平衡的意义：

为了保证树的高度与与节点总数成

logN

的关系，而一般的操作(add,delete,contains)都与树的高度有关,例如，堆是完全二叉树也是平衡二叉树，对堆的各种操作，时间复杂度都是

log(N)

插入：关注第一个不平衡的节点，调整原则是有序性+平衡性

插入就是在失败的查找的基础上再操作，插入过程中维持

有序性和平衡性

的核心操作：旋转。

我们只需要关注第一个不平衡的节点，然后再递归检查就OK，此时，只需要考察该节点与其孩子节点，其孩子的孩子节点(三代)的关系，因为这是导致不平衡的最小单元。

不平衡情形之一：LL

在节点的左孩子的左侧，插入新节点，导致节点失衡，LL，此时通过右旋转来解决，以中间节点为中心，旋转，这样能够同时满足有顺序性和平衡性。

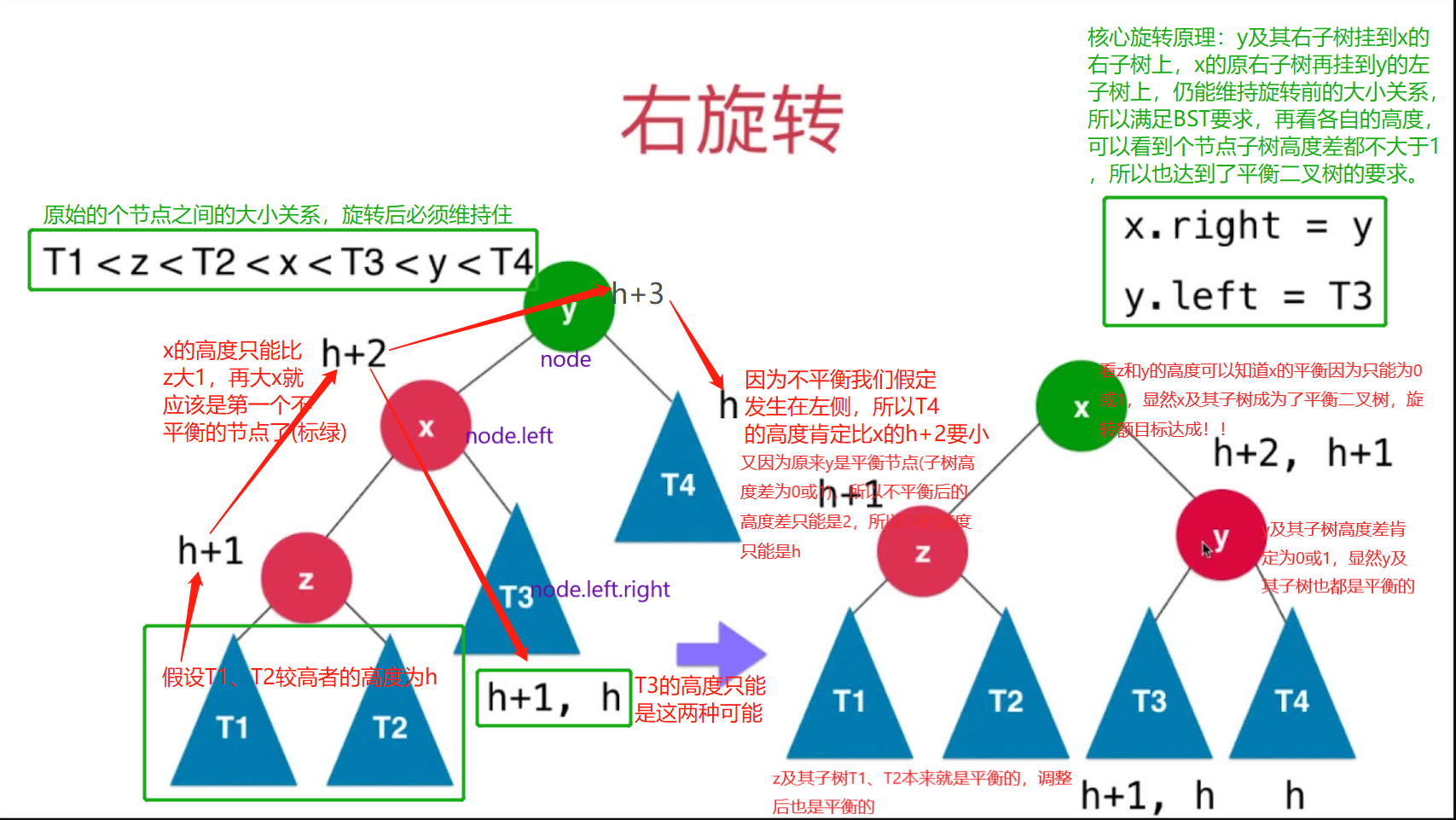
//y:第一个不平衡的节点，返回旋转后的根节点x
private Node rotateRight(Node y ){
Node x=y.left;
Node T3=x.right;
x.right=y;
y.left=T3;
//对x和y的位置进行调整，相应的高度也需要更新！！
y.height=calHeight(y);
x.height=calHeight(x);
return x;
}
private Node add(Node node,K key, V va){
//LL:在node的左侧的左侧添加的节点导致node不平衡。
if(balance>1&&calBalance(node,left)>=0){//calBalance:left的高度-right高度
return rotateRight(node);
}
}

不平衡情形之二：RR

在节点的右侧的右侧加入新节点，导致节点失衡，RR,采用左旋转解决，旋转中心为中间节点x.

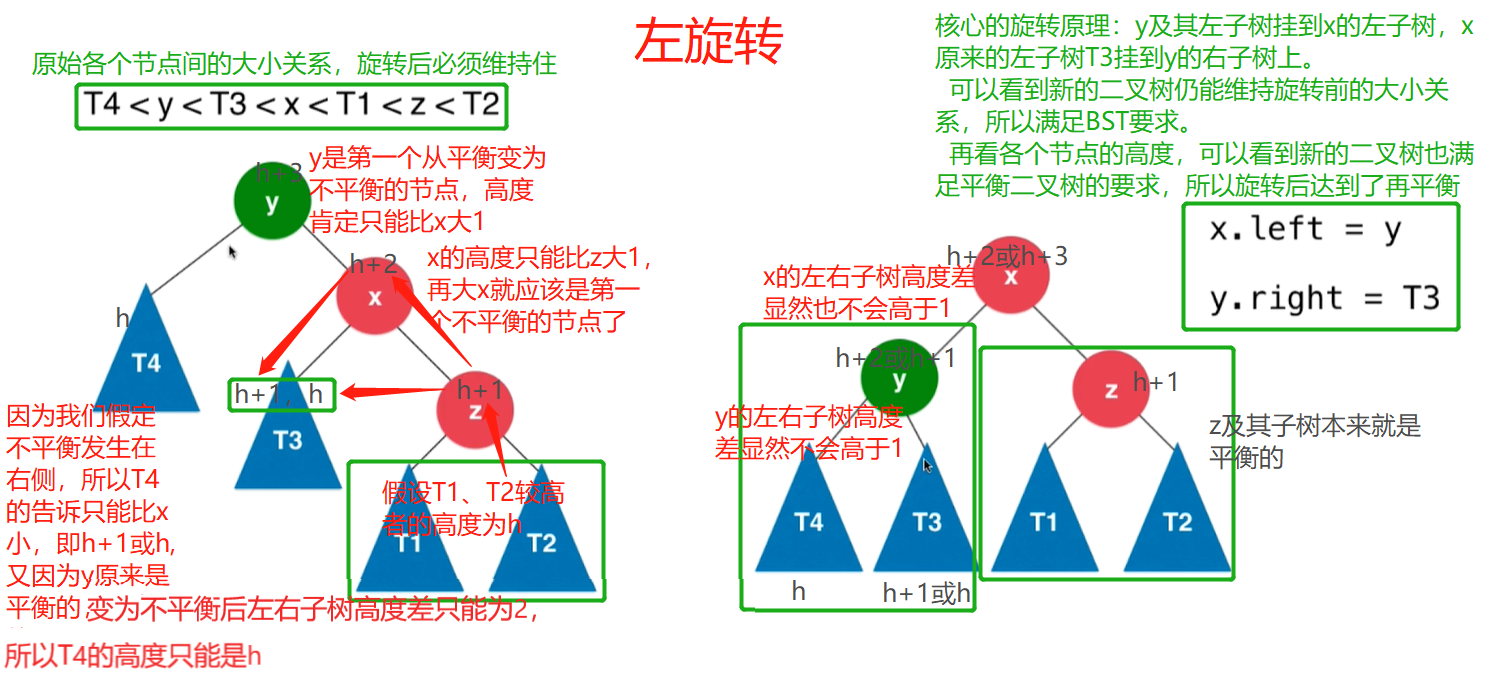
//y是第一个失衡的节点，返回旋转后的根节点
private Node rotateLeft(Node y){
Node x=y.right;
Node T3=x.left;
x.left=y;
y.right=T3;
//更新高度
x.height=calHeight(x);
y.height=calHeight(y);
return x;
}
private Node add(Node node, K key,V val){
//....
if(balance<-1&&calBalance(node.right)<=0){//balance的定义L-R
return rotateLeft(node);
}
}

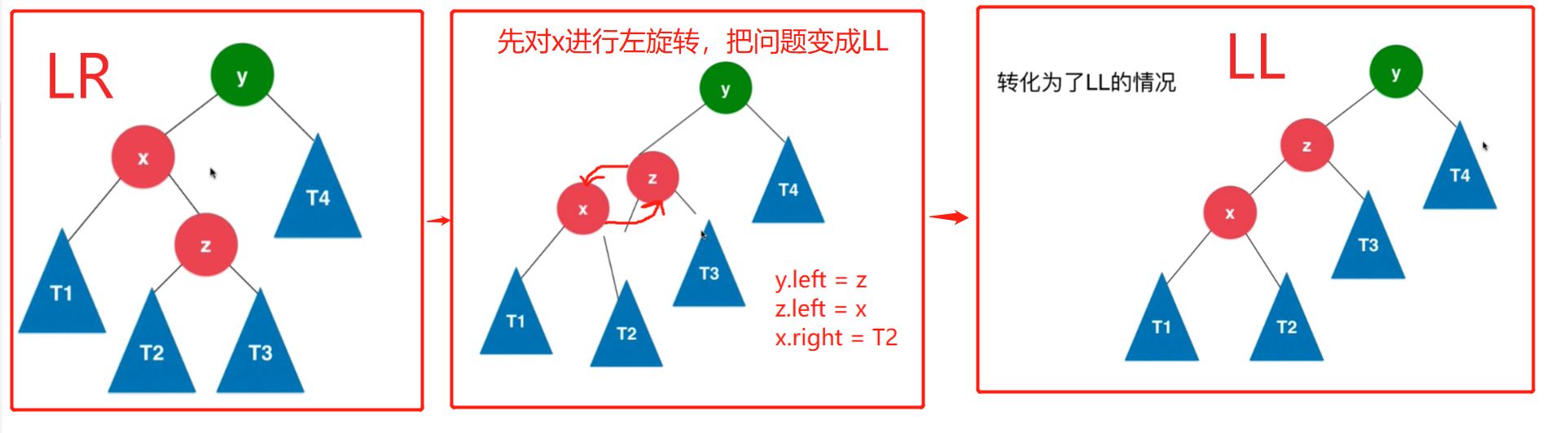
不平衡情形三：LR

在节点左孩子的右侧加入新节点(LR),导致AVL树失衡，调整方式：先左旋转(LL)后右旋转

private Node add(Node node,K key ,V val){//牢记要满足有序性+平衡性
//....
if(balance>1&&calBalance(node.left)<0){//以Z为中心。
node.left=rotateLeft(node.left);
return rotateRight(node);
}
//....
}

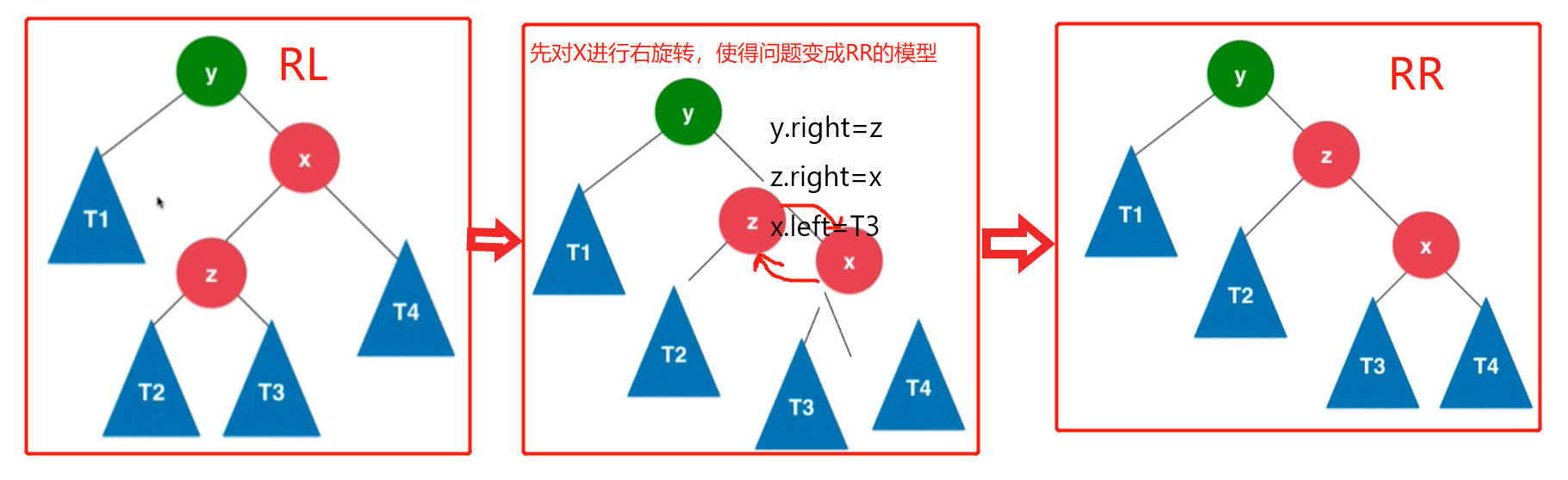
不平衡情形三：RL(上一种情形的对称）

在节点右孩子的左侧插入新节点导致树失衡，RL.调整方式：先右旋 ad8 转(RR)后左选择.

private Node add(Node node,K key ,V val){
//*...
if(balance<-1&&calBalance(Node.right)>0){
node.right=rotateRight(node.right);//z为中心。
return rotateLeft(node);
}
//....
}

删除：在BST(有序)的基础上再加入旋转操作。

BST的删除操作已经保证有序性了，再此基础上还需要考虑LL,LR,RR,RL着四种不平衡状态。

public V remove(K key){
Node node=getNode(root,key);
if(node!=null){
root=reomve(root,key);
return node.val;
}
return null;
}
private Node remove(Node node , K key){
//代码与BST的删除逻辑完全一样，只是为了调整平衡性，用retNode来保存删除后的头结点。

return rotateToReBalance(retNode);
}

//判断当前节点是否需要旋转，并执行相应的旋转操作。
private Node rotateToReBalance(Node node){
if(node==null) return null;
node.height=calHeight(node);
int blc=calBalance(node);
if(blc>1&&calBlanece(node.left)>=0){
return rotateRight(node);
}
if(blc<-1&&calBalance(node.right)<=0){
return rotateLeft(node);
}
if(blc>1&&calBalance(node.left)<0){
node.left=rotateLeft(node.left);
return rotateRight(node);
}
if(blc<-1&&calBalance(node.right)>0){
node.right=rotateRight(node.right);
return rotateLeft(node);
}
//不需要维护平衡，
return node;
}

AVL树的完整源码请点击这儿

AVL树缺点

• 平衡条件过于苛刻。
• 插入和删除的过程都需要验证平衡性(LL,RR,LR,RL)

基于AVL树的Set和Map。

红黑树：与2-3树是等价的

定义：

• 每个节点或者为红色、或者为黑色。
• 根节点为黑色。
• 每个叶子节点(最后的空节点)是黑色的，即null是黑色的，空树也是红黑树。
• 如果一个节点是红色的，那么他的孩子节点都是黑色的。
• 从任意一个节点到叶子节点，经过的黑色节点数相同。

2-3树,一种特殊的B树 1044 ，即m=3.

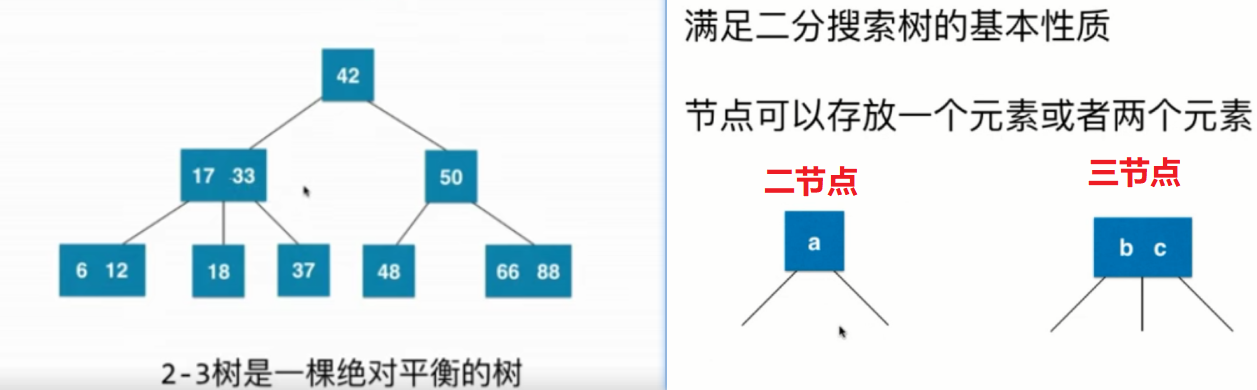
2-3树满足BST的基本性质(有序性)，节点可以存放一个元素(二节点)，也可以存放两个元素(三节点)。

性质：2-3树是一颗绝对平衡的树。从根节点到任意叶子节点之间具有相同的节点数。

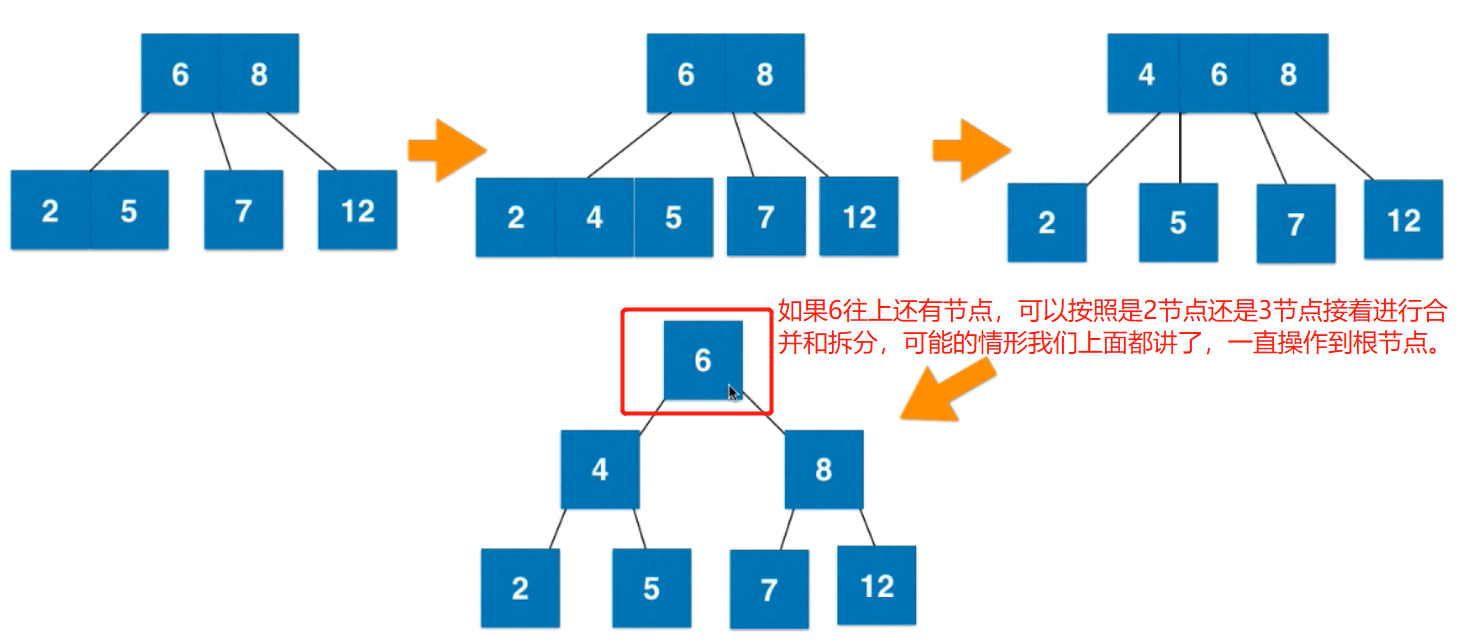
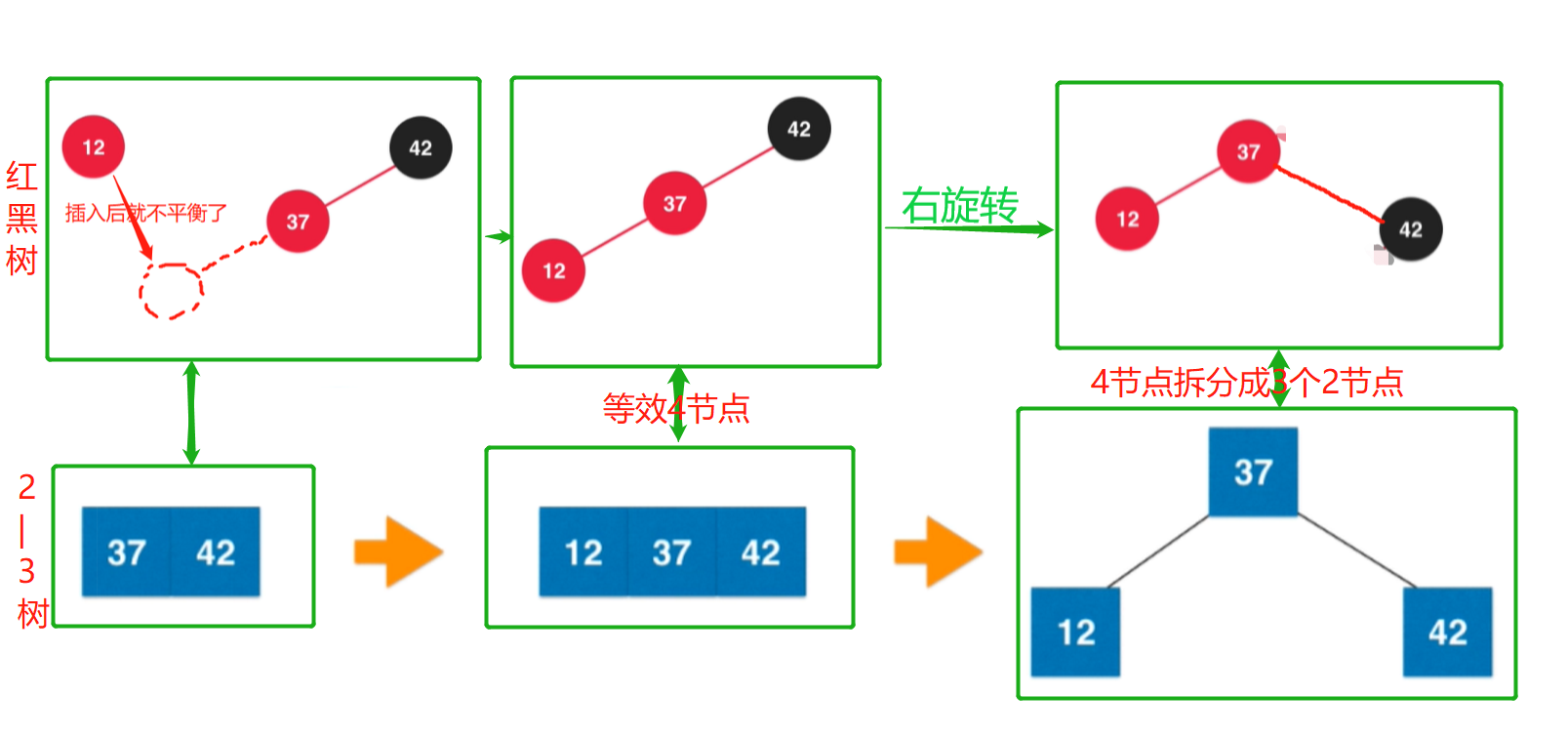
2-3的插入：与最后找到的叶子节点进行融合。

2-3树的插入过程就是不断形成3节点(则原来是2节点)、4节点(有4个分叉，即3个元素)的过程，然后拆分4节点为三个2节点的过程。目的：满足2-3绝对平衡的性质。

2-3树与红黑树的等价性

• 用单个黑色节点表示2-3树中的2节点
• 用红节点+父节点(颜色为黑)表表示2-3树的3节点，每个3节点会对应一个红节点,红色节点左倾。

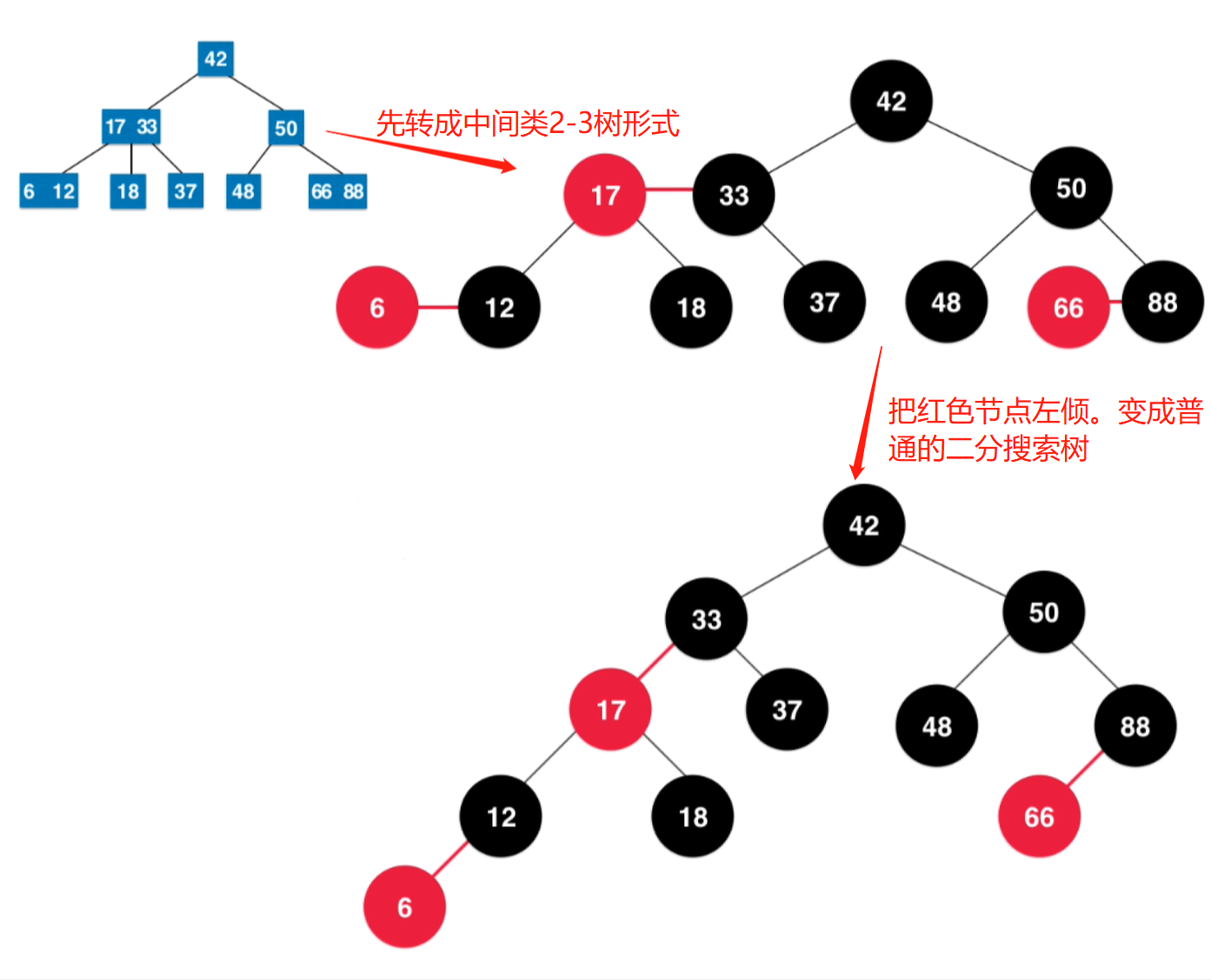
红黑树的插入(与2-3树类比)

当向2节点插入时，带插入位置是左节点，则不调整，是右节点则需要左旋转+颜色翻转，以满足红黑树的定义。

左旋转过程如下

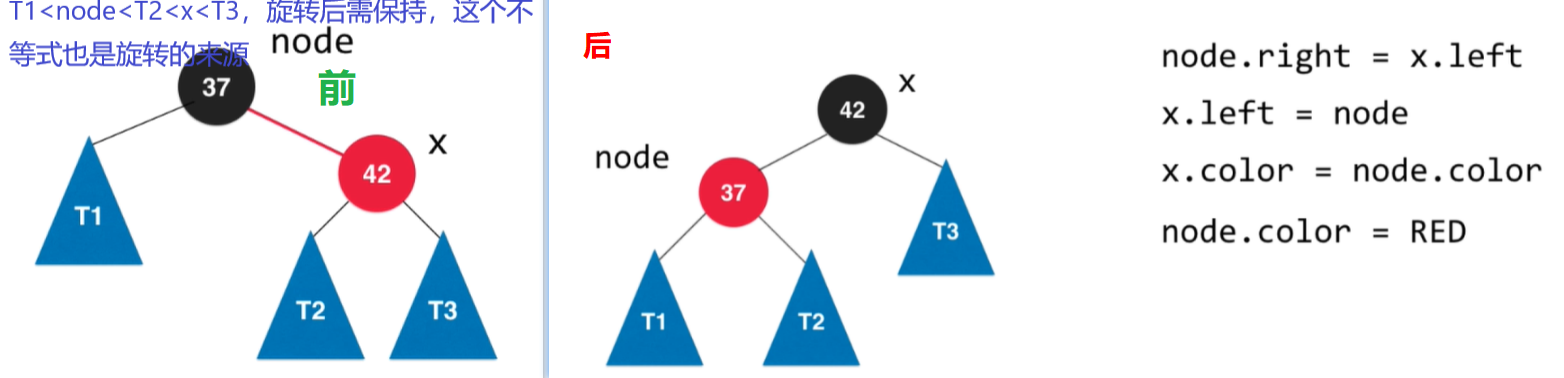
private Node rotateLeft(Node node) {
// 暂存节点
Node x = node.right;
// 左旋转
node.right = x.left;
x.left = node;
// 更新颜色
x.color = node.color;
node.color = RED;
return x;
}

private Node rotateRight(Node node) {
// 暂存节点
Node x = node.left;
Node T1 = x.right;
// 右旋转
node.left = T1;
x.right = node;
// 颜色更新
x.color = node.color;
node.color = RED;
return x;
}

当向3节点插入时，需要依次经过左旋转，右旋转，颜色翻转等过程。
红黑树的源码请点击这儿

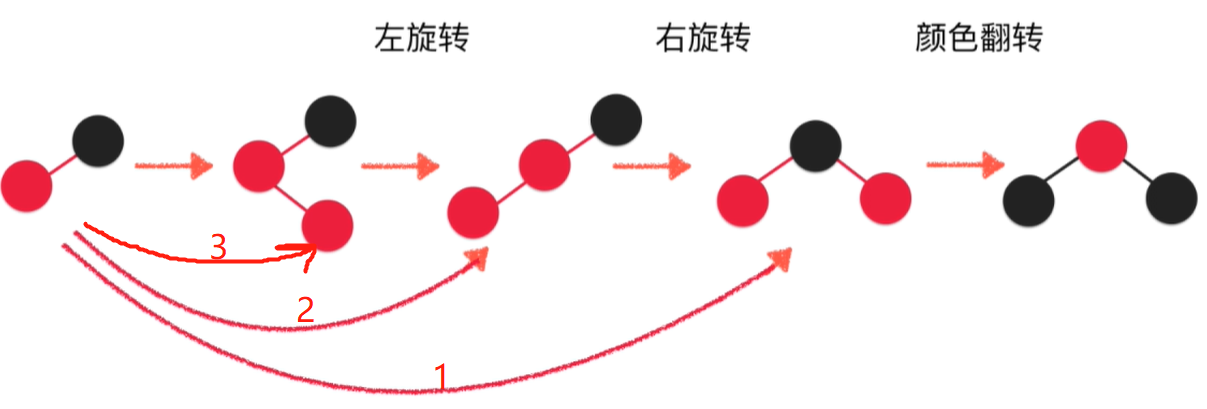
红黑树的统计性能更优

综合增删改查所有的操作，红黑树是平均性能最好的。AVL树的插入和删除过于复杂，查询较多时，AVL树比较合适。普通的BST对于有序数据就退化为链表。

红黑树更多

• 伸展树:考虑局部性原理的BST。
• JDK中的TreeMap和TreeSet就是基于红黑树实现的。