Leetcode543. 二叉树的直径 算法剖析

描述：

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过根结点。

leetcode oline

示例 :

给定二叉树

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

注意：两结点之间的路径长度是以它们之间边的数目表示。

这道题是求二叉树的深度的变形题目 大家都容易懂二叉树的深度是怎么求的 但是要彻底理解它的函数体内两个递归条件的步骤还是需要深入的

求二叉树的深度

核心代码是：

int deepth(Node *root){
if(root==NULL){
return 0;
}
int l = deepth(root->left);
int r = deepth(root->right);
return max(l,r)+1;
}

超简化版

class Solution {
public:
int maxDepth(TreeNode* root) {
if(root == NULL)
return 0;

return max(maxDepth(root->left), maxDepth(root->right)) + 1;
}
}；

本文写出了更为详细的调试代码 方便读者进行理解：
下面我们通过前序生成树的测试代码 来调求二叉树深度的递归遍历

#include<iostream>
using namespace std;

struct Node{
struct Node *left=NULL;
struct Node *right=NULL;
char data;
};

int i;

class Solution
{
public:
void CreatTree(Node *&node,string str){
if(i==str.length()){  //遍历结束
return;
}
if(str[i]=='#'){ //遇到空节点
i++;
return;
}
node = new Node;
node->data=str[i++];
CreatTree(node->left,str);
CreatTree(node->right,str);
}

//详解调试版
int deepth(Node *root){
if(root==nullptr){
cout<<"#"<<endl; //如果是空指针 返回高度为0
return 0;
}
cout<<"enter"<<root->data<<"'s left"<<endl; //进入以这个节点为根节点的左子树

int l = deepth(root->left); //此节点的左子树高度

cout<<"enter"<<root->data<<"'s right"<<endl;//进入以这个节点为根节点的右子树

int r = deepth(root->right); //此节点右子树高度

cout<<root->data<<"endl"<<endl; //左右子树递归完毕 执行这个语句
cout<<root->data<<" l= "<<l<<"r = "<<r<<endl; //计算出当前根节点的左右子树高度

return max(l,r)+1; //返回到上一层的数据是以此节点为根节点的左右子树高度大者+1
};

int main(){
Solution s1;
string str;
Node *root = nullptr;
cin>>str;
i=0;
s1.CreatTree(root, str);
int sum = s1.deepth(r);
cout<<sum<<endl;
}

4当我们建造一颗图为下面的二叉树的时候：

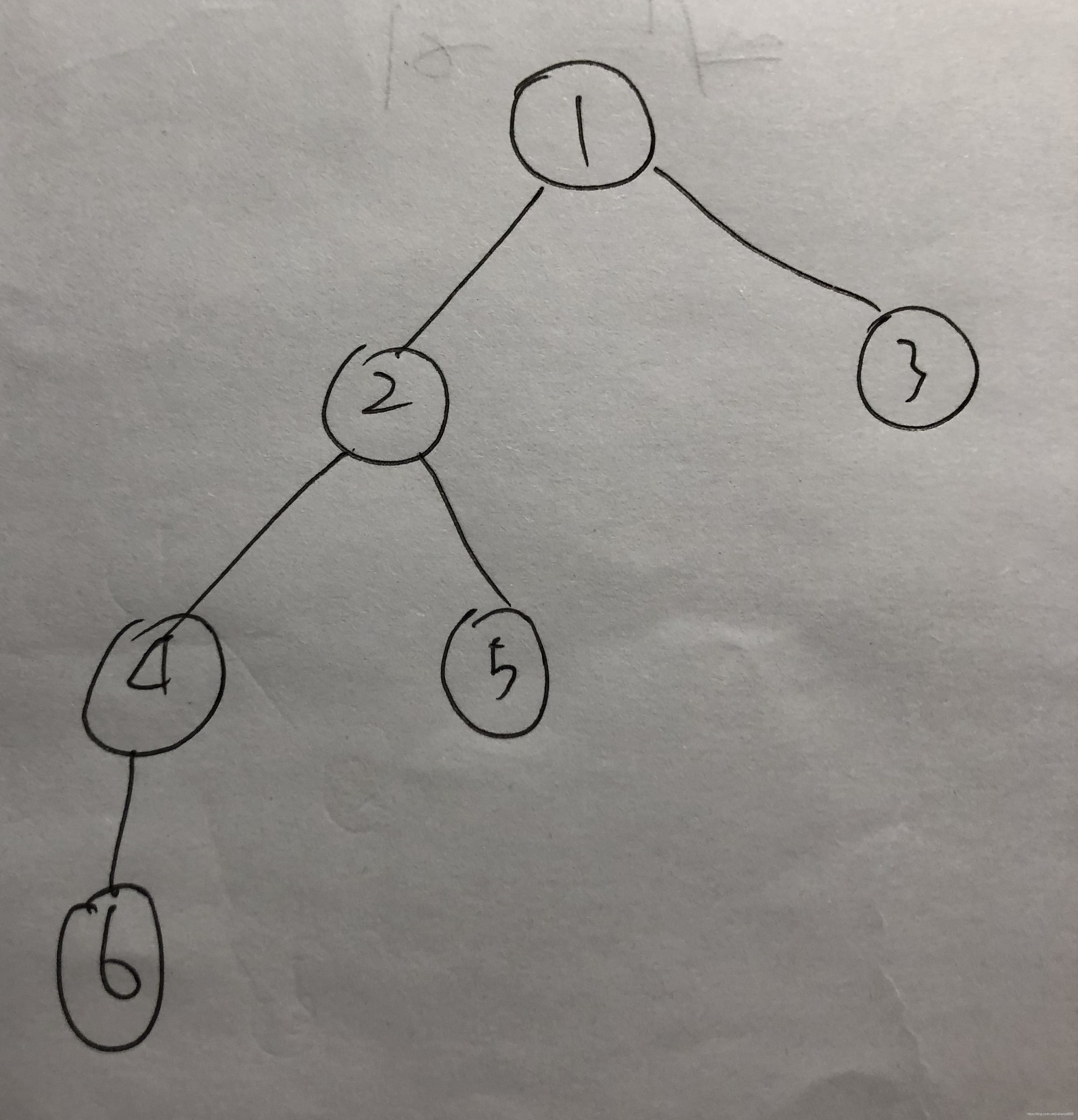
我们在控制窗口输入

1246###5##3##

输出：

enter1's left
enter2's left
enter4's left
enter6's left
#
enter6's right
#
6endl
6 l= 0r = 0
enter4's right
#
4endl
4 l= 1r = 0
enter2's right
enter5's left
#
enter5's right
#
5endl
5 l= 0r = 0
2endl
2 l= 2r = 1
enter1's right
enter3's left
#
enter3's right
#
3endl
3 l= 0r = 0
1endl
1 l= 3r = 1
4

解析：
*二叉树在往左的递归中会一直跑（递归）

enter1’s left
enter2’s left
enter4’s left
enter6’s left`

直到遇到null的指针为止 再返回null的上一层的右子树

enter6’s right

进行同样的遍历
如果左右子树均访问过，则会进入到return 语句(结束）
return返回一个以当前节点为根节点的左右子树+1 的高度（最大高度）

6endl
6 l= 0 r = 0 （return 1）

再退回上一层 进入其右子树 反复进行同样的遍历 把上次计算return的数进行保存并且进行比较

enter4’s right

读者可以根据上面的代码自己进行逐步调试 印象更深刻

回归本题

本题不是最大高度 而是经过的路径最长 这代表着不一定是经过根节点的 那么每一个节点都有可能是我们所求的子树的根节点
总而言之 需要每个节点都判断其左右子树的和为最大值并保存比较

现在再来理解这道题目：

由于我们需要知道每个节点的左右子树的高度这里需要注意的是，我们并不是直接将左右子树的深度加起来，是在还没有进行加1的时候就做加法运算，因为本题算的是

边数

若只有一个节点，return之后是1为深度的数，但是最小直径是0.

tip：

采用引用的方式，将每个节点的最大的dis进行比较并且保存较大者即可

int Deepth(TreeNode *root,int& dis）

/**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/

class Solution {
public:
int diameterOfBinaryTree(TreeNode* root) {
int dis = 0;
int sum =Deepth(root,dis);
return dis;
}

int Deepth(TreeNode *root,int& dis){
if(root==nullptr){
return 0;
}
int l = Deepth(root->left ,dis);
int r = Deepth(root->right,dis);
dis = max(dis,l+r);
return max(l,r)+1;
}
};

• 点赞
• 收藏
• 分享
• 文章举报