文章目录

• 深入理解数制的设计原理
• 原码、反码和补码的数轴解释
• 现在用的补码和上面说到的反码不同在哪呢？

深入理解数制的设计原理

  虽然在这里不介绍各种进制之间的转换和关系，但是接下来我们会见到的是如何从其他进制（这里用人们最容易理解的十进制）得到二进制的很多重要的思想

原码、反码和补码的数轴解释

1.对于无符号数我们特别好理解用数轴表示为

它的数值在数轴上是递增的，而且没有负数，我们非常好理解，所以没必要花更多的时间在无符号数这里。
 
2.运算总是要负数的，那我们尝试着去表示负数，最快想到的就是符号/数值表示法，如图

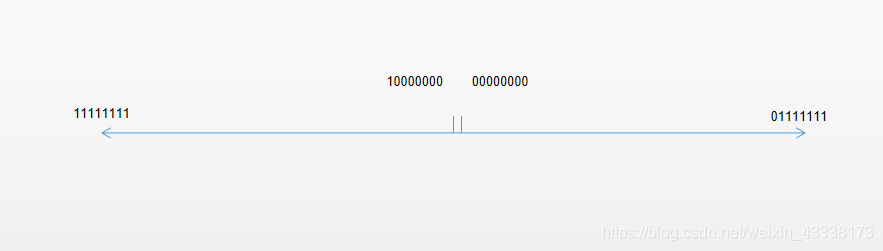
就是用第一位数表示符号（我们选择0开头的是整数1开头的是负数）其他的位表示数值的大小（数值越大表示正得或者负得越多），这对人类的大脑依然是很友好的。但是这种表示法，在运算的时候并不是很便利，比如在减法中我们要比较大下来判断运算之后保留的是负号还是正号。同时在没有减法器时要做减法就只能用一个整数加上一个负数（显然也不能直接运算）。
那么我们还需要改进…
 
3.思考下面的坐标图

这个图和第一张图中二进制无符号数的坐标图基本上是保持一致的
在十进制中我们很熟悉一个规律：0+999 = 1+998 = 2+997 = … = 499+500
既然我们要用500到999的数来表示-499到-0，同时同时500到999的数与0到499的数又通过以上的规律得到关联，所以我们可以对其如下定义：所有大于499小于1000的数X对999求补（也就是用999减去这个数） 得到数就是==-X==，得到如下表示法:
 
4.

在这种表示法中0和999都是表示0的，但是这并没什么不好的，所以我们可以将它推广到二进制中，如下图： 
值得注意的是：在二进制中是对11111111求补，因为1是二进制中最大的数.同时由于二进制的特殊性对二进制数求补和对该数求反是一样的结果

那这种表示能不解决我们之前留下来的问题呢？
我们认为他是可以的，比如：65-117(01000001- 01110101)可以怎么运算呢？
  首先看作是65 + （-117），那么进行的运算就是01000001(整数求补不变) + 10001010(对01110101求补得到)，直接运算得到11001011(这个数就是答案的补数,就是-52)。所以说在这种表示法下可以用加法器实现减法，同时不需要比较正数和负数数值上的大小省去了很多的计算成本。
现在对二进制求补后得到的数被称作是反码（因为它确实可以通过求反得到）
所以这种表示法被叫做反码表示法
 

现在用的补码和上面说到的反码不同在哪呢？

（依旧以十进制为例）这又说到了0和999都用于表示0的问题了，我们的解决办法就是求补之后还加上1（也就相当于对1000求补）使得表示负数的数值整体往左边移了一位，如图（二进制）：

它依然可以完成上面反码表示法能完成的功能，可以说变得跟好的（因为他又解决了一个问题）。
我们因此也为这种表示法命名补码表示法（补了个1）

• 点赞 1
• 收藏
• 分享
• 文章举报