62.不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

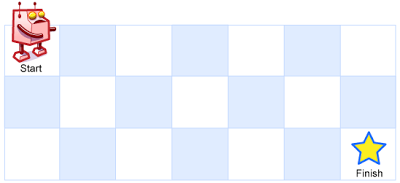
例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3
输出: 28

思路分析：

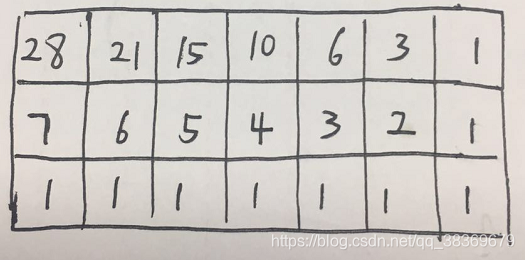
本题是典型的使用动态规划的题，最下方一行和最右一列的路径数都为1，其余的格子从右下角开始每个格子的路径数等于右边格子路径数和下方格子路径数之和。dp[i][j]=dp[i+1][j]+dp[i][j+1]。 代码如下：

class Solution {
public int uniquePaths(int m, int n) {
if(m==1 || n==1) return 1;
int[][] dp=new int[m]
;
for(int i=0;i<n;i++){
dp[m-1][i]=1;
}
for(int i=0;i<m;i++){
dp[i][n-1]=1;
}
for(int i=m-2;i>=0;i--){
for(int j=n-2;j>=0;j--){
dp[i][j]=dp[i+1][j]+dp[i][j+1];
}
}
return dp[0][0];
}
}

相关问题： LeetCode 63.不同路径 II