LeetCode62/63. 不同路径问题（python）

62. 不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

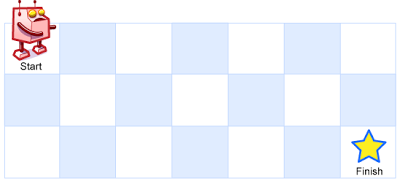
例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

[code]输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 2:

[code]输入: m = 7, n = 3
输出: 28

 解题思路：

动态规划

机器人每次只能向下或者向右移动一步，所以到达每一格的路径，等于左面格子的路径数加上方格子的路径数；

初始矩阵[[1，1，1]，[1，1，1]，[1，1，1]]，“路径记录”矩阵[[1，1，1]，[1，2，3]，[1，3，6]]

所以从左上角到右下角的路径数最后就记录在右下角矩阵中。

代码：

[code]class Solution:
def uniquePaths(self, m: int, n: int) -> int:
grid = [[1 for _ in range(n)] for _ in range(m)]
for i in range(1, m):
for j in range(1, n):
grid[i][j] = grid[i-1][j] + grid[i][j-1]

return grid[m-1][n-1]

63. 不同路径 II

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 

1

 和 

0

 来表示。

说明：m 和 n 的值均不超过 100。

示例 1:

输入:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
输出: 2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 [code]2

条不同的路径： 1. 向右 -> 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 -> 向右[/code]

解题思路：

同上题一样，也是动态规划问题，只不过要考虑障碍物；

首先我们将题中所述的矩阵0与1交换（0， 1 =1， 0），对第一行和第一列单独处理，行或列中出现障碍物，则后面位置就全写为0（必然走不到）；

接着对矩阵进行遍历从[1，1]，遍历到右下角元素，当当前位置的值为1时，当前位置的值等于左侧位置的值加上方位置的值，遍历到最后，右下角位置的值即为所求，返回右下角的值。

代码：

[code]class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
m = len(obstacleGrid)
n = len(obstacleGrid[0])

if obstacleGrid[0][0] == 1 or obstacleGrid[m-1][n-1] == 1:
return 0

for j in range(n):
if obstacleGrid[0][j] == 0:
obstacleGrid[0][j] = 1
elif obstacleGrid[0][j] == 1:
for k in range(j, n):
obstacleGrid[0][k] = 0
break

for i in range(1, m):
if obstacleGrid[i][0] == 0:
obstacleGrid[i][0] = 1
elif obstacleGrid[i][0] == 1:
for k in range(i, m):
obstacleGrid[k][0] = 0
break

for i in range(1, m):
for j in range(1, n):
if obstacleGrid[i][j] == 0:
obstacleGrid[i][j] = 1
elif obstacleGrid[i][j] == 1:
obstacleGrid[i][j] = 0
if obstacleGrid[i][j] == 1:
obstacleGrid[i][j] = obstacleGrid[i-1][j] + obstacleGrid[i][j-1]

return obstacleGrid[m-1][n-1]

总结：

第一个问题的处理上基本没什么问题；

对于存在障碍物的问题，在边界问题的处理上有些繁琐，可能是思路的问题，因为我顺着第一个问题做的，明天看看评论大神们都怎么做的，有空再回来修改一下。