第一课 神经网络和深度学习

第二周 神经网络基础

概要:
构建神经网络时,有些技巧是相当重要的.

可以不直接使用for循环来遍历整个训练集.

神经网络计算过程中通常有一个正向过程和一个反向过程.

Logistic Regression 是一个用于二分分类的算法.

网易云课堂传送门: https://mooc.study.163.com/course/2001281002#/info

2.1 二分分类

例子:

例如有一张图片的输入,想要识别此图的标签;

1(cat)vs 0(non cat)

计算机保存图片 要保存三个独立矩阵,分别对应 red green blue 三个颜色通道.

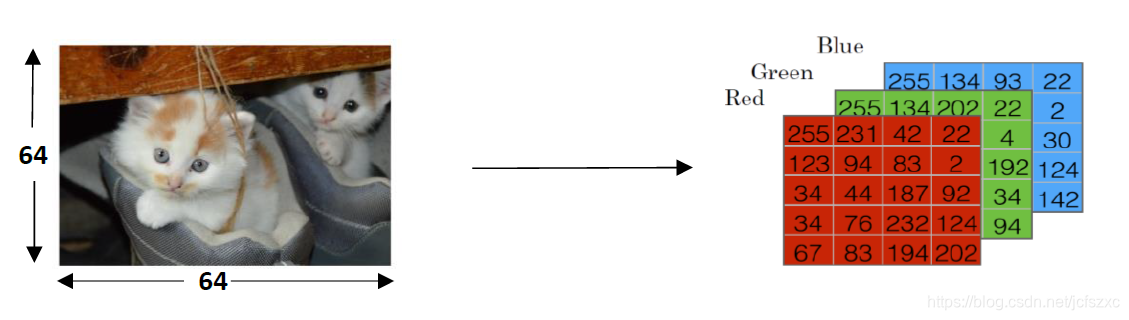
把这些像素亮度值提出来,放入一个特征向量 x. 如果图片是6464的 那么向量 x 的总维度就是6464*3 因为这是三个矩阵的元素数量 对于这个例子,数字是12888. 我们用 nx = 12288来表示输入特征向量 x 的维度 有时候为了简洁 会直接用小写的 n.

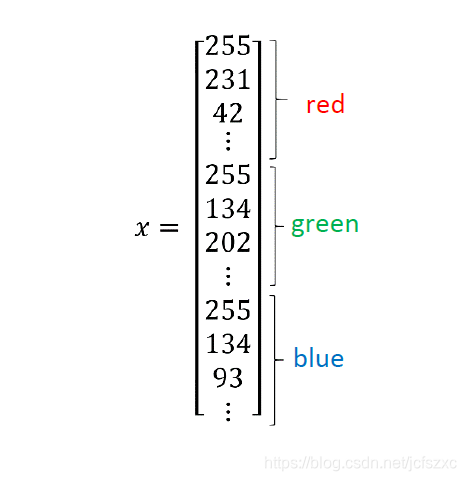
目标:

在二分分类问题中 目标是训练出一个分类器,它以图片的特征向量 x 作为输入,预测输出结果标签 y 是1还是0, 也就是预测图片是否有猫.

常用符号:

(x,y) —— 表示一个单独的样本

x 是 nx 维的特征向量

标签 y 值为0或1

训练集由 m 个训练样本构成,用小写的 m 来表示训练样本的个数。

有时候为了强调可以写作：

m = m_train —— 训练集的个数
m = m_test —— 测试集的样本数
(x(1),y(1)x^{(1)},y^{(1)}x(1),y(1)) —— 样本1的输入和输出
(x(2),y(2)x^{(2)},y^{(2)}x(2),y(2)) —— 样本2的输入和输出
(x(m),y(m)x^{(m)},y^{(m)}x(m),y(m)) —— 样本m的输入和输出
α\alphaα —— 学习率

用更紧凑的符号来表示训练集：
我们定义一个矩阵 用大写的 X 表示 它由训练集中的 x(1)x^{(1)}x(1) 、x(2)x^{(2)}x(2) 这些组成 像这样写成矩阵的列
现在我们把 x(1)x^{(1)}x(1) 放进矩阵的第一列, x(2)x^{(2)}x(2) 是第二列… x^(m) 是第 m 列, 最后得到矩阵 X ,这个矩阵有 m 列, nx 行, 有时候会表示为转置矩阵.

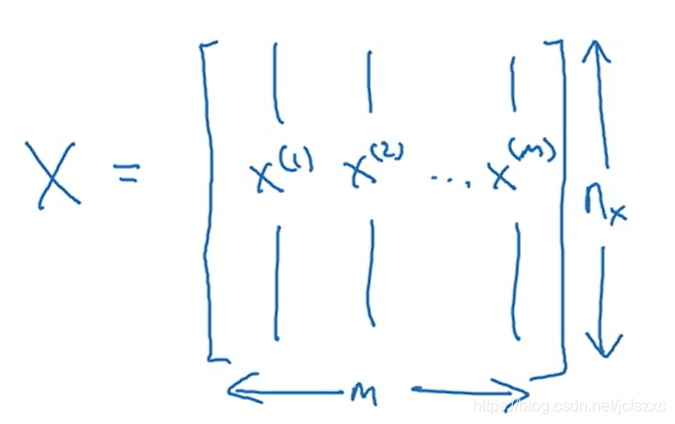
(构建神经网络时 一般用第一个约定形式,会让构建过程简单得多.)
输出标签 y 也放入一个矩阵, 我们定义 Y 是 y(1)y^{(1)}y(1), y(2)y^{(2)}y(2)…, y(m)y^{(m)}y(m), 这里的 Y 是一个 1 * m 矩阵.

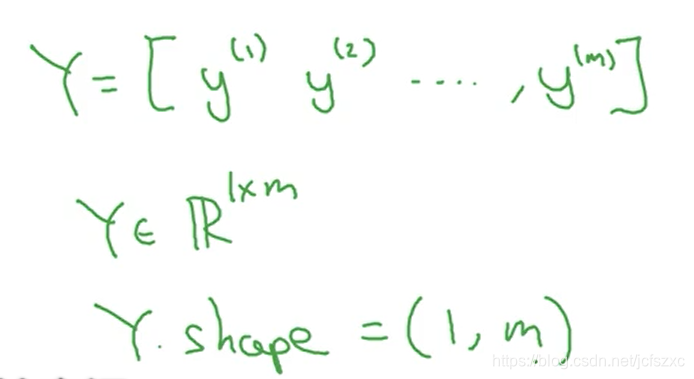
python中 用 X.shape 用来输出矩阵的维度即( nx ,m ). 这就是如何将训练样本 即输入 x 用矩阵表示,同样地 在python里 Y.shape 等于(1 , m).

提示: 好的惯例符号能够将不同训练样本的数据联系起来

2.2 Logistic 回归

这是一个学习算法,用在监督学习问题中. 当输出标签是0或1时,这是一个二元分类问题.

例子:

已知输入特征向量 x 可能是一张图,你需要识别出它是否是猫图. 需要一个算法可以给出一个预测值.

y^\widehat{y}y​ 记作对 y 的预测.更正式地说,希望 y^\widehat{y}y​ 是一个概率.

当输入特征 x 满足条件时, y 就是1,所以换句话说,如果 x 是图片, 我们希望 y^\widehat{y}y​ 可以反馈这是一张猫图的概率.

x 正如我们上面说过的. 是一个 n_x 维向量, 已知 Logistic 回归的参数是 w , w 也是一个 n_x 维向量. 而 b 就是一个实数,已知输入 x 和参数 w 和 b. 我们要如何计算输出预测 y^\widehat{y}y​

线性回归不是一个非常好的二元分类算法.因为我们希望 y^\widehat{y}y​ 是 y = 1 的概率. 所以 y^\widehat{y}y​ 应该介于0和1之间. 但是线性代数的值可能会比1大得多,或者是负数,这样的概率是没有意义的.

所以在 Logistic 回归中, 我们的输出变成 y^\widehat{y}y​ 等于 sigmoid 函数作用在 z=wTx+bz = w^T x + bz=wTx+b 这个量上.

即: y^=σ(wTx+b)\widehat{y}=\sigma(w^T x + b)y​=σ(wTx+b)

sigmoid函数:

y=11+e−z y=\frac{1}{1+e^{-z}} y=1+e−z1​

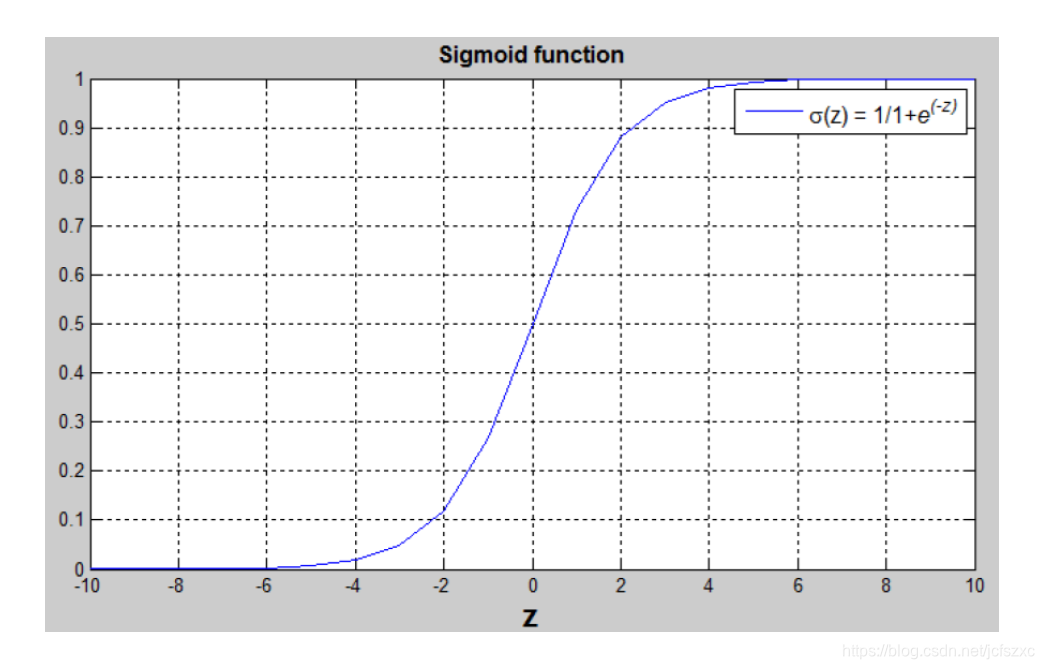
分析: z 是常数,如果 z 非常大,那么 e−ze^{-z}e−z 就很接近0, 那么 σ(z)\sigma(z)σ(z) 就很接近1. 相反,如果z非常小,那么 σ(z)\sigma(z)σ(z) 就会很接近0. 所以当实现 logistic 回归时,要做的是学习参数 w 和 b. 所以 y^\widehat{y}y​ 变成了对于 y = 1 概率的比较好的估计.

接下来,关于 w 和 b 需要我们定义一个成本函数.

2.3 Logistic 回归损失函数

为了训练 logistic regression 模型的参数 w 以及 b 需要定义一个成本函数.

为了让模型来通过学习调整参数. 需要给一个 m 个样本的训练集,想通过在训练集 找到参数 w 和 b 来得到输出.

对训练集中的预测值,将它写成 y^(i)\widehat{y}^{(i)}y​(i) 我们希望它接近于在训练集中的 y(i)y^{(i)}y(i) 值.

为了让上面的方程更详细一些 需要说明上面这里定义的 y(i)y^{(i)}y(i) 是对一个训练样本 x 来说的 对于每个训练样本 使用这些带有圆括号的上标 方便引用说明 还有区分样本, 你的训练样本 (i) 对应的预测值是 y^(i)\widehat{y}^{(i)}y​(i) ,是用训练样本通过 sigmoid 函数作用到 z=wTx+bz = w^T x + bz=wTx+b 得到的. 即 y^=σ(wTx+b)\widehat{y}=\sigma(w^T x + b)y​=σ(wTx+b).

我们将使用这个符号约定.就是这个上标来指明数据 表示 x 或者 y 或者 z 和第 i 个训练样本有关,和第 i 个样本有关.

损失函数:

损失函数,或者叫做误差函数. 他们可以用来衡量算法的运行情况. 方便梯度下降.

定义损失函数为: L(y^,y)=y(i)⋅log⁡y^(i)+(1−y(i))log⁡(1−y^(i))L(\widehat{y},y)=y^{(i)}\cdot\log{\widehat{y}^{(i)}}+(1-y^{(i)})\log{(1-\widehat{y}^{(i)})}L(y​,y)=y(i)⋅logy​(i)+(1−y(i))log(1−y​(i))

最后,损失函数是在单个训练样本中定义的 它衡量了在单个训练样本上的表现. 下面我们要定义一个成本函数, 它衡量的是在全体训练样本上的表现.这个成本函数 J 根据之前得到的两个参数 w 和 b

成本函数: J(w,b)=1m⋅∑i=1mL(y^(i),y(i))=−1m⋅∑i=1m[y(i)⋅log⁡y^(i)+(1−y(i))log⁡(1−y^(i))]J(w,b)=\frac1m\cdot\sum^m_{i=1}L(\widehat{y}^{(i)},y^{(i)})=-\frac1m\cdot\sum^m_{i=1}[y^{(i)}\cdot\log{\widehat{y}^{(i)}}+(1-y^{(i)})\log{(1-\widehat{y}^{(i)})}]J(w,b)=m1​⋅∑i=1m​L(y​(i),y(i))=−m1​⋅∑i=1m​[y(i)⋅logy​(i)+(1−y(i))log(1−y​(i))]

损失函数只适用于单个训练样本, 成本函数基于参数的总成本,所以在训练 Logistic 回归模型时,我们要找到合适的参数 w 和 b ,让下面这里的成本函数 J 尽可能地小.

Logistic 回归可以被看作一个很小的神经网络.

2.4 梯度下降法

梯度下降法用来训练或学习训练机上的参数 w 和 b.

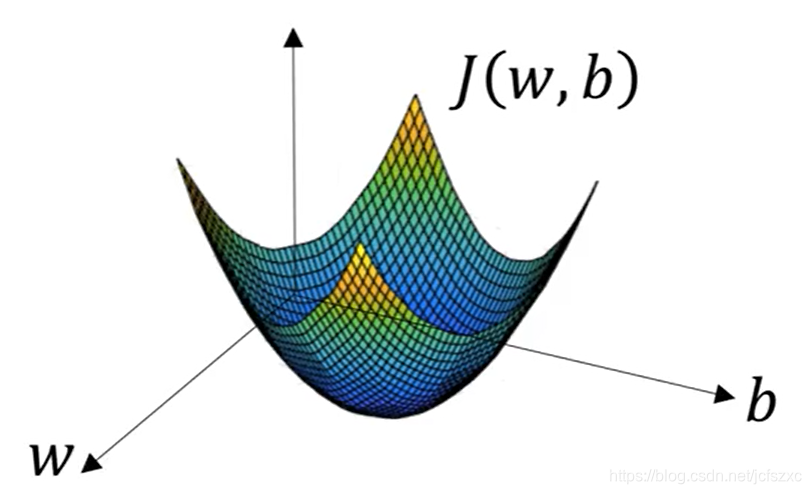
根据函数图像可知,函数 J(w,b) 是一个曲面凸函数.

为了找到更好的参数值,我们要做的就是用某初始值初始化 w 和 b.

对于 Logistic Regression 来说,一般任意的初始化都是可以的,无论在哪里初始化,都可以大致达到同一个位置.

梯度下降法所做的就是 从初始点开始 朝最陡的下坡方向走一步. 即为梯度下降的一次迭代. 不断接近最优解.

不断更新 w 和 b 的值. α 用来控制每一次迭代或者梯度下降法中的步长.

w:=w−αdJ(w)dww:=w−α⋅dw w:=w-\alpha\frac{d{J(w)}}{dw}\\ w:=w-\alpha \cdot dw w:=w−αdwdJ(w)​w:=w−α⋅dw

2.5 & 2.6 导数及其例子

掌握微积分的最基础知识即可(略)

2.7 计算图

一个神经网络的计算都是按照 前向或反向传播过程来实现的.

首先计算出神经网络的输出,紧接着进行一个反向传输操作.后者我们用来计算出对应的梯度或者导数.

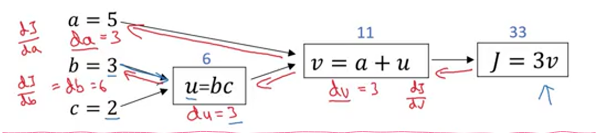
2.8 计算图的导数计算

一个计算流程图就是正向 或者说从左到右的计算 来计算成本函数 j ,然后反向从右到左计算导数.

2.9 Logistic 回归中的梯度下降法

我们在logistc回归中，需要做的就是变换参数w和b的值来最小化损失函数

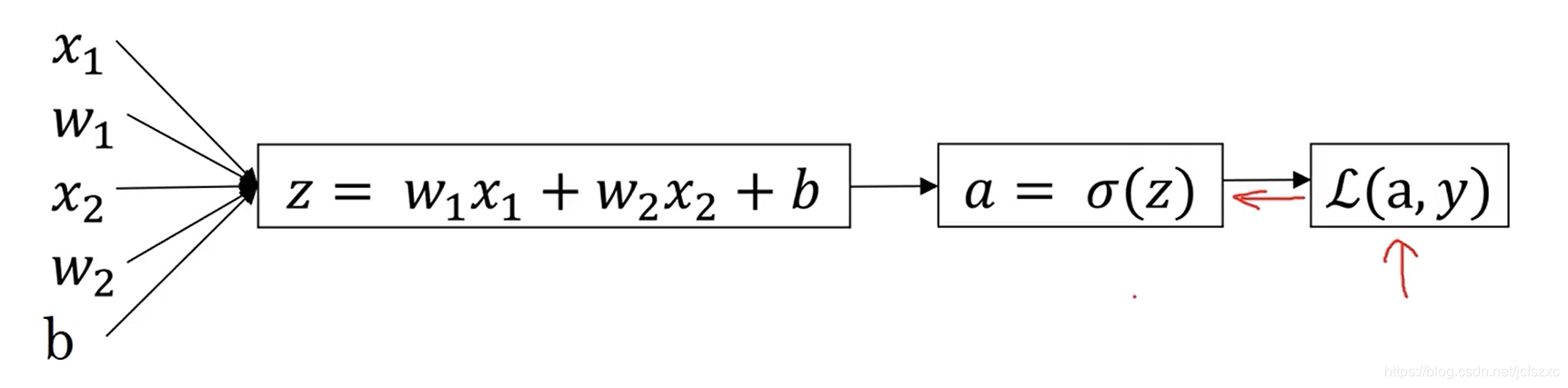
2.10 m 个样本的梯度下降

普通计算方法的两个缺点:

第一个 for 循环: 遍历 m 个训练样本的小循环

第二个 for 循环: 遍历所有特征的 for 循环

原因:

在代码中显式地使用 for 循环会使算法很低效

解决方法:

通过向量化来帮助代码摆脱这些显式的 for 循环

2.11 & 2.12 向量化及其更多的例子

什么是向量化?

在 Logistic 回归中,需要去计算 z=wTx+bz=w^Tx+bz=wTx+b, w 是列向量 x 也是列向量. 如果你有很多的特征,他们就是非常大的向量. 所以 w 和 x 都是 R 内的 nx 维向量.

python 中的 numpy 模块

在python用numpy函数. z=np.dot(w,x)+b 计算 wTx+bw^Tx+bwTx+b

向量化数据的计算速度会比非向量化数据的计算速度要快上一个数量级

所以尽可能地通过使用这些能去掉显式 for 循环的函数,这样python的numpy能够充分利用并行化去更快的计算.这点对CPU和GPU上面计算都是成立的.

熟练掌握numpy库的各种函数,可以让代码中不再使用 for 显式循环.

2.13 & 2.14 向量化 Logistic 回归及其的梯度输出

向量化可以显著加速代码,只要熟练掌握理解矩阵的运算和python的numpy函数即可.

2.15 Python 中的广播

广播是一种可以让 Python 代码段执行得更快的手段. 可以自动复制扩充填满矩阵,令计算继续.

2.16 注意事项:

不要将秩为1的数组和1×n的矩阵混用,容易产生错误.

Numpy的Python基础知识

说明:

• 将使用 Python3
• 尽量避免使用 for 循环和 while 循环.

目的:

• 能使用 iPython 笔记本电脑
• 能使用 numpy 函数 和 numpy 矩阵/向量操作
• 理解"广播"的概念
• 能够矢量化代码

关于iPython笔记本

iPython笔记本是嵌入在网页中的交互式编码环境。

编写代码后，可以通过按“SHIFT”+“ENTER”或单击笔记本上方栏中的“运行单元格”（用播放符号表示）来运行单元格。

1 - 用 numpy 构建基本功能

Numpy 是 Python 中科学计算的主要软件包。它由一个大型社区维护（www.numpy.org）。在本练习中，您将学习几个关键的 numpy 函数，如 np.exp ，np.log 和 np.reshape() 。您将需要知道如何将这些功能用于将来的分配。

1.1 - sigmoid 函数, np.exp()

sigmoid(x)=11+e−xsigmoid(x)=\frac{1}{1+e^{-x}}sigmoid(x)=1+e−x1​ 有时也被称为逻辑函数. 它是一种非线性函数, 不仅用于机器学习 (Logistic回归), 还用于深度学习.

我们很少在深度学习中使用“math”库，因为函数的输入是实数。在深度学习中，我们主要使用矩阵和向量。这就是numpy更有用的原因。

事实上, 如果x=(x1,x2,…xn)x=(x_1,x_2,\dots x_n)x=(x1​,x2​,…xn​)是行向量, np.exp() 可以将指数函数应用于 x 的每个元素, 因此输出将会是 np.exp(x)=(ex1,ex2,⋯exn)np.exp(x)=(e^{x_1},e^{x_2},\cdots e^{x_n})np.exp(x)=(ex1​,ex2​,⋯exn​)
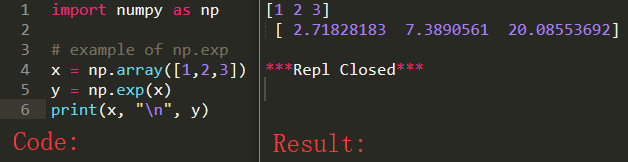
如果需要有关numpy功能的更多信息，建议您查看官方文档。

练习:
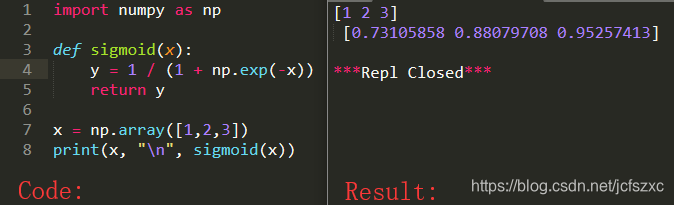
使用 numpy 实现 sigmoid 函数.
说明:
x 现在可以是实数, 矢量或矩阵. 我们在 numpy 中用来表示这些形状(向量, 矩阵…)的数据结构称为 numpy 数组.

1.2 - Sigmoid 梯度

我们需要使用反向传播来计算梯度来优化损失函数, 让我们来编写第一个导函数.

练习:
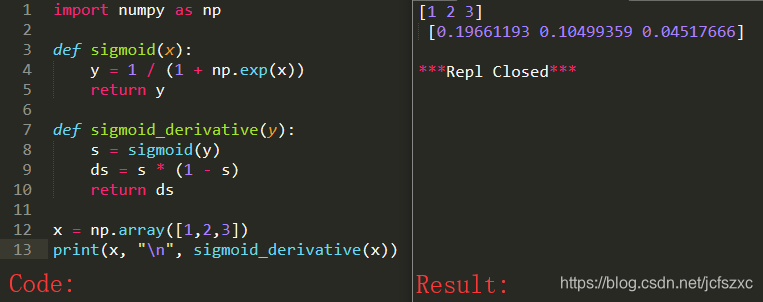
实现函数 sigmoid_grad() 以计算 sigmoid 函数相对于其输入 x 的梯度. 公式是:
sigmoidderivative(x)=σ′(x)=σ(x)(1−σ(x))sigmoid_derivative(x) = \sigma'(x)=\sigma(x)(1-\sigma(x))sigmoidd​erivative(x)=σ′(x)=σ(x)(1−σ(x))
我们通过下面这两步来实现:

1. 将 s 设置为 x 的sigmoid. 你会发现 sigmoid(x) 是很有用的.
2. 计算 σ′(x)=s(1−s)\sigma'(x)=s(1-s)σ′(x)=s(1−s)

1.3 - 重塑数组

深度学习中使用的两个常见的 numpy 函数是 np.shape 和 np.reshape().

• X.shape 用于获得矩阵/向量X的形状(维度).
• X.reshape(…) 用于将 X 重塑为其他维度.

例如, 在计算机科学中, 图像由 3D 阵列形状表示 (length,height,depth)(length, height, depth)(length,height,depth) 但是将图像作为算法输入时, 将其转换为形状矢量(length∗height∗depth,1)(length*height*depth,1)(length∗height∗depth,1) 换句话说, 在将 3D 阵列"展开"或重新整型为一维向量.

练习:
实现 image2vector() 接受形状输入(lenght,height,3)(lenght,height,3)(lenght,height,3) 并返回形状矢量(length∗height∗3,1)(length*height*3,1)(length∗height∗3,1), 例:

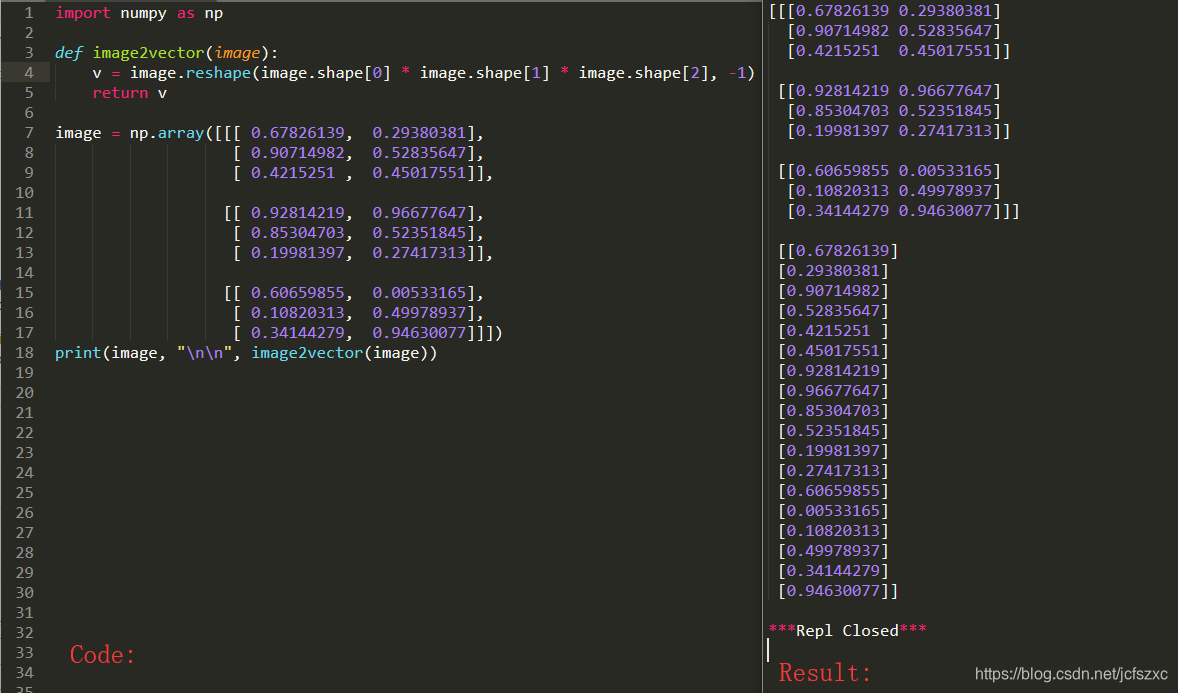
1.4 - 规范行

我们在机器学习和深度学习中使用的另一种常用技术是规范化我们的数据。它通常会带来更好的性能，因为梯度下降在归一化后收敛得更快。在这里，通过归一化我们的意思是将x改为x∣∣x∣∣\frac x{||x||}∣∣x∣∣x​（将x的每一行向量除以其范数）。例:

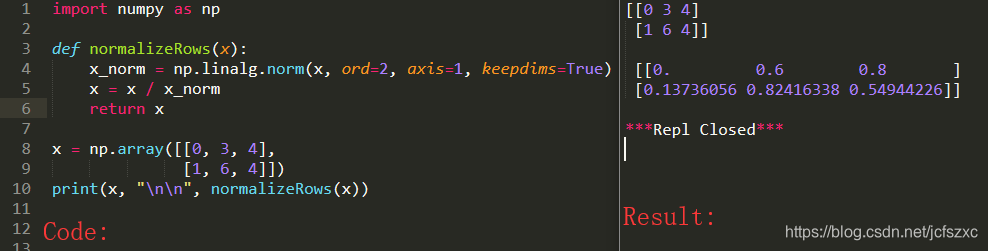
注意:

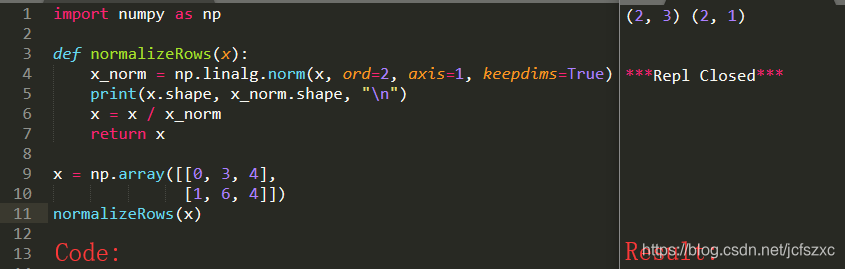
可以发现, x 和 x_norm 的相撞是不同的. 但是他们却仍然可以正常运算, 它是如何工作的呢? 这就是接下来要讲的广播.

1.5 - 广播和 softmax 函数

在 numpy 中理解的一个非常重要的概念是“广播”。它对于在不同形状的阵列之间执行数学运算非常有用。有关广播的详细信息，可以阅读官方广播文档。

练习:
使用 numpy 实现 softmax 函数。可以将 softmax 视为当算法需要对两个或更多类进行分类时使用的规范化函数。您将在本专业的第二个课程中了解有关 softmax 的更多信息。

对于一维矢量来说:
for x∈R1×nx \in R^{1\times n}x∈R1×n, softmax(x)=softmax([x1,x2,⋯xn])softmax(x)=softmax([x_1, x_2,\cdots x_n])softmax(x)=softmax([x1​,x2​,⋯xn​])

对于向量来说: (3)softmax(x)=softmax[x11x12x13⋯x1nx21x22x23⋯x2n⋯⋯⋯⋯⋯xm1xm2xm3⋯xmn]=[ex11∑jex1jex12∑jex1jex13∑jex1j⋯ex1n∑jex1jex21∑jex2jex22∑jex2jex23∑jex2j⋯ex2n∑jex2j⋯⋯⋯⋯⋯exm1∑jexmjexm2∑jexmjexm3∑jexmj⋯exmn∑jexmj] softmax(x)=softmax\left[ \begin{matrix} x_{11} & x_{12} & x_{13} & \cdots & x_{1n}\\ x_{21} & x_{22} & x_{23} & \cdots & x_{2n}\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ x_{m1} & x_{m2} & x_{m3} & \cdots & x_{mn}\\ \end{matrix} \right] \tag{3}=\left[ \begin{matrix} \frac{e^{x_{11}}}{\sum_je^{x_1j}} & {e^{x_{12}}}{\sum_je^{x_1j}} & {e^{x_{13}}}{\sum_je^{x_1j}} & \cdots & {e^{x_{1n}}}{\sum_je^{x_1j}}\\ \frac{e^{x_{21}}}{\sum_je^{x_2j}} & {e^{x_{22}}}{\sum_je^{x_2j}} & {e^{x_{23}}}{\sum_je^{x_2j}} & \cdots & {e^{x_{2n}}}{\sum_je^{x_2j}}\\ \cdots & \cdots & \cdots & \cdots & \cdots\\ \frac{e^{x_{m1}}}{\sum_je^{x_mj}} & {e^{x_{m2}}}{\sum_je^{x_mj}} & {e^{x_{m3}}}{\sum_je^{x_mj}} & \cdots & {e^{x_{mn}}}{\sum_je^{x_mj}}\\ \end{matrix} \right]softmax(x)=softmax⎣⎢⎢⎡​x11​x21​⋯xm1​​x12​x22​⋯xm2​​x13​x23​⋯xm3​​⋯⋯⋯⋯​x1n​x2n​⋯xmn​​⎦⎥⎥⎤​=⎣⎢⎢⎢⎢⎡​∑j​ex1​jex11​​∑j​ex2​jex21​​⋯∑j​exm​jexm1​​​ex12​∑j​ex1​jex22​∑j​ex2​j⋯exm2​∑j​exm​j​ex13​∑j​ex1​jex23​∑j​ex2​j⋯exm3​∑j​exm​j​⋯⋯⋯⋯​ex1n​∑j​ex1​jex2n​∑j​ex2​j⋯exmn​∑j​exm​j​⎦⎥⎥⎥⎥⎤​(3)

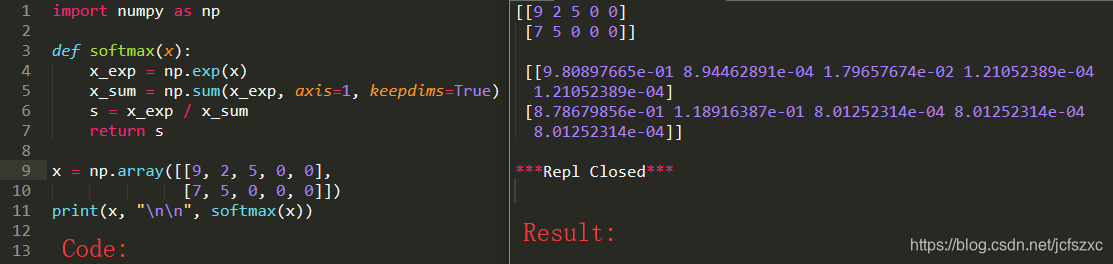
可以发现 x_exp 的形状为 (2, 5), x_sum 的形状为 (2, 1). x_exp / x_sum 是由于python广播在起作用, 广播能将单行或单列自动扩充.

2) 矢量化

向量化代码进行运算可以加快运算速度

2.1 - 实现 L1 和 L2 损失函数

练习:
实现 L1 损失的 numpy 矢量化版本. 你会发现函数 abs(x) (求 x 的绝对值)很有用.
提醒:

• 损失用于评估模型的性能。损失越大, 说明预测值y^\widehat{y}y​ 和真实值 (y)(y)(y) 的差别。在深度学习中，您可以使用Gradient Descent等优化算法来训练模型并最大限度地降低成本。
  L1(y^,y)=∑i=0m∣y(i)−y^(i)∣L_1(\widehat{y},y)=\sum^{m}_{i=0}|y^{(i)}-\widehat{y}^{(i)}|L1​(y​,y)=i=0∑m​∣y(i)−y​(i)∣
  

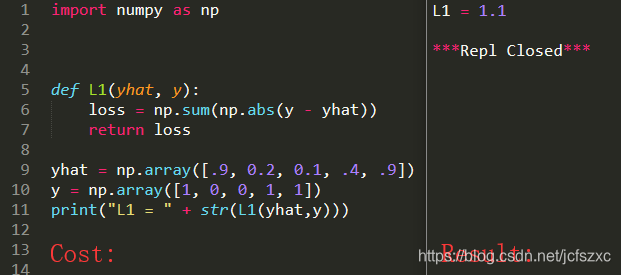
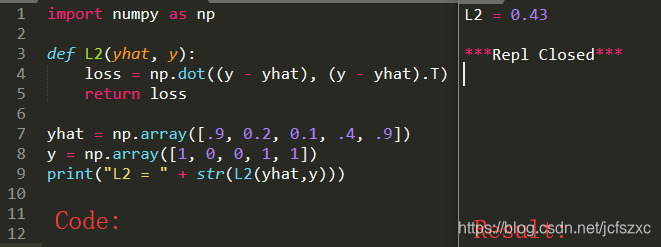
L2(y^,y)=∑i=0m(y(i)−y^(i))2L_2(\widehat{y},y)=\sum^m_{i=0}(y^{(i)}-\widehat{y}^{(i)})^2L2​(y​,y)=i=0∑m​(y(i)−y​(i))2