矩阵分解 SVD分解

在认识SVD之前，先来学习两个相关的概念：正交矩阵和酉矩阵。

如果

，则

阶实矩阵

称为正交矩阵。而酉矩阵是正交矩阵往复数域上的推广。

判断正交矩阵和酉矩阵的充分必要条件是：

。或者说正交矩阵和酉矩阵的共轭转置和它的

逆矩阵相等。

对任意

矩阵

，都能被奇异值分解为



其中

是

的正交矩阵，

是

的正交矩阵，

是由

个沿对角线从大到小排列的奇异值

组成的方阵，

就是矩阵

的秩。奇异值分解是一种正交矩阵分解法。

1.前言

一般提到特征值分解(eigenvalue decomposition)或者奇异值分解(singular value decomposition)，大多数同学脑海里的第一反应就是一大堆矩阵以及数学计算方法。确实，学校学习阶段，不管是学线性代数或者矩阵分析，对于这部分内容，或者说绝大部分内容，老师一上来都是吧啦吧啦给你一堆定理推论或者公理，然后就是哗啦哗啦一堆公式出来，告诉你怎么计算。最后再讲个一两道例题，这个知识点就算讲完了。至于这些公式的来龙去脉，尤其是这些公式定理在实际中有什么用，能解决什么实际问题，老师很少有谈及。所以大家普遍反映对于线性代数矩阵分析这类课程，觉得特别枯燥。学完以后，即使考试过了会做题，随便再问几个为什么，基本也是一脸懵逼的状态。至少我当年的学习经历就是这样滴。

等出学校以后发现，实际上在学校学的这些内容，都是非常有用而且有明确的数学或者物理意义的。在学校的时候，老师一般都会告诉你这个很有用，但是给解释清楚的，确实很少。今天，我就按照自己的理解，试图给大家将特征值分解与SVD的来龙去脉解释清楚。如果有哪里不对或者理解有偏差，还请大家海涵并指出。

2.特征值、特征向量、特征值分解

特征值特征向量是贯穿整个线性代数与矩阵分析的主线之一。那么特征值特征向量除了课本上公式的描述以外，到底有什么实际意义呢？

在http://blog.csdn.net/bitcarmanlee/article/details/52067985一文中，为大家解释了一个核心观点：矩阵是线性空间里的变换的描述。在有了这个认识的基础上，咱们接着往下。

特征值的定义很简单：Ax=λx。其中A为矩阵,λ为特征值，x为特征向量。不知道大家想过没有：为什么一个向量，跟一个数相乘的效果，与跟一个矩阵的效果相乘是一样的呢？

这得用到我们先前的结论：矩阵是线性空间里的变换的描述。矩阵A与向量相乘，本质上对向量x进行一次线性转换（旋转或拉伸），而该转换的效果为常数c乘以向量x（即只进行拉伸）。当我们求特征值与特征向量的时候，就是为了求矩阵A能使哪些向量（特征向量）只发生拉伸，而拉伸的程度，自然就是特征值λ了。

如果还有同学没有看懂，再引用wiki百科上的一个描述：

N 维非零向量 x 是 N×N 的矩阵 A 的特征向量，当且仅当下式成立：Ax=λx

其中λ为一标量，称为x对应的特征值。也称x为特征值λ对应的特征向量。也即特征向量被施以线性变换A只会使向量伸长或缩短而其方向不被改变。

对于一个矩阵A，有一组特征向量；再将这组向量进行正交化单位化，也就是我们学过的Schmidt正交化，就能得到一组正交单位向量。特征值分解，就是将矩阵A分解为如下方式：

A=QΣQ−1

这其中，Q是矩阵A的特征向量组成的矩阵，Σ则是一个对角阵，对角线上的元素就是特征值。

为了描述更清楚，引用网络上的一部分描述：

对于一个矩阵M:

M=[3001]

它对应的线性变换是下面的形式：



因为这个矩阵M乘以一个向量(x,y)的结果是：

[3001][xy]=[3xy]

上面的矩阵是对称的，所以这个变换是一个对x，y轴的方向一个拉伸变换（每一个对角线上的元素将会对一个维度进行拉伸变换，当值>1时，是拉长，当值<1时时缩短），当矩阵不是对称的时候，假如说矩阵是下面的样子：

[3011]

它所描述的变换是下面的样子：



这其实是在平面上对一个轴进行的拉伸变换（如蓝色的箭头所示），在图中，蓝色的箭头是一个最主要的变化方向（变化方向可能有不止一个），如果我们想要描述好一个变换，那我们就描述好这个变换主要的变化方向就好了。反过头来看看之前特征值分解的式子，分解得到的Σ矩阵是一个对角阵，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）

当矩阵是高维的情况下，那么这个矩阵就是高维空间下的一个线性变换，这个线性变化可能没法通过图片来表示，但是可以想象，这个变换也同样有很多的变换方向，我们通过特征值分解得到的前N个特征向量，那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向，就可以近似这个矩阵（变换）。也就是之前说的：提取这个矩阵最重要的特征。总结一下，特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么，可以将每一个特征向量理解为一个线性的子空间，我们可以利用这些线性的子空间干很多的事情。不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。

以上的图片及内容来自LeftNotEasy的博客内容。感觉描述还是比较到位。

3.SVD分解

前面啰啰嗦嗦说了这么多基础，终于轮到咱们的主角：SVD登场了。

首先我们来看看奇异值的定义：对于一个矩阵A，有：(ATA)ν=λν

那么向量v就是A的右奇异向量。并且：

奇异值：σi=λi−−√

左奇异向量：μi=1σiAνi

咱们前面讲了那么多的特征值与特征值分解，而且特征值分解是一个提取矩阵特征很不错的方法。但是，特征值分解最大的问题是只能针对方阵，即n∗n的矩阵。而在实际应用场景中，大部分不是这种矩阵。举个最简单的例子，关系型数据库中的某一张表的数据存储结构就类似于一个二维矩阵，假设这个表有m行，有n个字段，那么这个表数据矩阵的规模就是m∗n。很明显，在绝大部分情况下，m与n并不相等。如果对这个矩阵要进行特征提取，特征值分解的方法显然就行不通了。那么此时，就是SVD分解发挥威力的时候。

假设A是一个m∗n阶矩阵，如此则存在一个分解使得

A=UΣVT

其中U是m×m阶酉矩阵；Σ是m×n阶非负实数对角矩阵；而VT，即V的共轭转置，是n×n阶酉矩阵。这样的分解就称作M的奇异值分解。Σ对角线上的元素Σi,i即为M的奇异值。而且一般来说，我们会将Σ上的值按从大到小的顺序排列。

通过上面对SVD的简单描述，不难发现，SVD解决了特征值分解中只能针对方阵而没法对更一般矩阵进行分解的问题。所以在实际中，SVD的应用场景比特征值分解更为通用与广泛。

将将上面的SVD分解用一个图形象表示如下



其中各矩阵的规模已经在上面描述过了。

截止到这里为止，很多同学会有疑问了：你这不吃饱了撑得。好好的一个矩阵A，你这为毛要将他表示成三个矩阵。这三个矩阵的规模，一点也不比原来矩阵的规模小好么。而且还要做两次矩阵的乘法。要知道，矩阵乘法可是个复杂度为O(n3)的运算。

同志们别急，请接着往下看。

如果按照之前那种方式分解，肯定是没有任何好处的。矩阵规模大了，还要做乘法运算。关键是奇异值有个牛逼的性质：在大部分情况下，当我们把矩阵Σ里的奇异值按从大到小的顺序呢排列以后，很容易就会发现，奇异值σ减小的速度特别快。在很多时候，前10%甚至前1%的奇异值的和就占了全部奇异值和的99%以上。换句话说，大部分奇异值都很小，基本没什么卵用。。。既然这样，那我们就可以用前面r个奇异值来对这个矩阵做近似。于是，SVD也可以这么写：

Am×n≈Um×rΣr×rVr×n

其中，r≪m，r≪n。如果用另外一幅图描述这个过程，如下图：



看了上面这幅图，同学们是不是就恍然大悟：原来的那个大矩阵A，原来可以用右边的那三个小矩阵来表示。当然如果r越大，跟原来的矩阵相似度就越高。如果r=n，那得到的就是原来的矩阵A。但是这样存储与计算的成本就越高。所以，实际在使用SVD的时候，需要我们根据不同的业务场景与需求还有资源情况，合理选择r的大小。本质而言，就是在计算精度与空间时间成本之间做个折中。

4.SVD分解的应用

SVD在实际中应用非常广泛，每个应用场景再单写一篇文章都没有问题。这里我们先不做过多的展开，先举两个最重要的方面。为了方便后面的描述，先把SVD的近似表达式再拎出来

Am×n≈Um×rΣr×rVr×n

1.降维

通过上面的式子很容易看出，原来矩阵A的特征有n维。而经过SVD分解之后，完全可以用前r个非零奇异值对应的奇异向量表示矩阵A的主要特征。这样，就天然起到了降维的作用。

2.压缩

还是看上面的式子，再结合第三部分的图，也很容易看出，经过SVD分解以后，要表示原来的大矩阵A，我们只需要存U，Σ，V三个较小的矩阵的即可。而这三个较小矩阵的规模，加起来也远远小于原有矩阵A。这样，就天然起到了压缩的作用。

5.奇异值的计算：

奇异值的计算是一个难题，是一个O(N^3)的算法。在单机的情况下当然是没问题的，matlab在一秒钟内就可以算出1000 * 1000的矩阵的所有奇异值，但是当矩阵的规模增长的时候，计算的复杂度呈3次方增长，就需要并行计算参与了。Google的吴军老师在数学之美系列谈到SVD的时候，说起Google实现了SVD的并行化算法，说这是对人类的一个贡献，但是也没有给出具体的计算规模，也没有给出太多有价值的信息。

其实SVD还是可以用并行的方式去实现的，在解大规模的矩阵的时候，一般使用迭代的方法，当矩阵的规模很大（比如说上亿）的时候，迭代的次数也可能会上亿次，如果使用Map-Reduce框架去解，则每次Map-Reduce完成的时候，都会涉及到写文件、读文件的操作。个人猜测Google云计算体系中除了Map-Reduce以外应该还有类似于MPI的计算模型，也就是节点之间是保持通信，数据是常驻在内存中的，这种计算模型比Map-Reduce在解决迭代次数非常多的时候，要快了很多倍。

Lanczos迭代就是一种解对称方阵部分特征值的方法（之前谈到了，解A’*
A得到的对称方阵的特征值就是解A的右奇异向量），是将一个对称的方程化为一个三对角矩阵再进行求解。按网上的一些文献来看，Google应该是用这种方法去做的奇异值分解的。请见Wikipedia上面的一些引用的论文，如果理解了那些论文，也“几乎”可以做出一个SVD了。

由于奇异值的计算是一个很枯燥，纯数学的过程，而且前人的研究成果（论文中）几乎已经把整个程序的流程图给出来了。

6.奇异值与主成分分析（PCA）

主成分分析在上一节里面也讲了一些，这里主要谈谈如何用SVD去解PCA的问题。PCA的问题其实是一个基的变换，使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量，我们在讲一个东西的稳定性的时候，往往说要减小方差，如果一个模型的方差很大，那就说明模型不稳定了。但是对于我们用于机器学习的数据（主要是训练数据），方差大才有意义，不然输入的数据都是同一个点，那方差就为0了，这样输入的多个数据就等同于一个数据了。以下面这张图为例子：





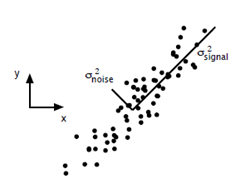
这个假设是一个摄像机采集一个物体运动得到的图片，上面的点表示物体运动的位置，假如我们想要用一条直线去拟合这些点，那我们会选择什么方向的线呢？当然是图上标有signal的那条线。如果我们把这些点单纯的投影到x轴或者y轴上，最后在x轴与y轴上得到的方差是相似的（因为这些点的趋势是在45度左右的方向，所以投影到x轴或者y轴上都是类似的），如果我们使用原来的xy坐标系去看这些点，容易看不出来这些点真正的方向是什么。但是如果我们进行坐标系的变化，横轴变成了signal的方向，纵轴变成了noise的方向，则就很容易发现什么方向的方差大，什么方向的方差小了。

一般来说，方差大的方向是信号的方向，方差小的方向是噪声的方向，我们在数据挖掘中或者数字信号处理中，往往要提高信号与噪声的比例，也就是信噪比。对上图来说，如果我们只保留signal方向的数据，也可以对原数据进行不错的近似了。

PCA的全部工作简单点说，就是对原始的空间中顺序地找一组相互正交的坐标轴，第一个轴是使得方差最大的，第二个轴是在与第一个轴正交的平面中使得方差最大的，第三个轴是在与第1、2个轴正交的平面中方差最大的，这样假设在N维空间中，我们可以找到N个这样的坐标轴，我们取前r个去近似这个空间，这样就从一个N维的空间压缩到r维的空间了，但是我们选择的r个坐标轴能够使得空间的压缩使得数据的损失最小。

还是假设我们矩阵每一行表示一个样本，每一列表示一个feature，用矩阵的语言来表示，将一个m * n的矩阵A的进行坐标轴的变化，P就是一个变换的矩阵从一个N维的空间变换到另一个N维的空间，在空间中就会进行一些类似于旋转、拉伸的变化。





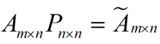
而将一个m * n的矩阵A变换成一个m * r的矩阵，这样就会使得本来有n个feature的，变成了有r个feature了（r < n)，这r个其实就是对n个feature的一种提炼，我们就把这个称为feature的压缩。用数学语言表示就是：





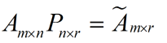
但是这个怎么和SVD扯上关系呢？之前谈到，SVD得出的奇异向量也是从奇异值由大到小排列的，按PCA的观点来看，就是方差最大的坐标轴就是第一个奇异向量，方差次大的坐标轴就是第二个奇异向量…我们回忆一下之前得到的SVD式子：





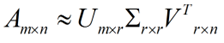
在矩阵的两边同时乘上一个矩阵V，由于V是一个正交的矩阵，所以V转置乘以V得到单位阵I，所以可以化成后面的式子





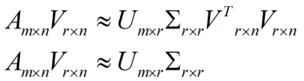
将后面的式子与A * P那个m * n的矩阵变换为m * r的矩阵的式子对照看看，在这里，其实V就是P，也就是一个变化的向量。这里是将一个m * n 的矩阵压缩到一个m * r的矩阵，也就是对列进行压缩，如果我们想对行进行压缩（在PCA的观点下，对行进行压缩可以理解为，将一些相似的sample合并在一起，或者将一些没有太大价值的sample去掉）怎么办呢？同样我们写出一个通用的行压缩例子：





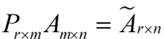
这样就从一个m行的矩阵压缩到一个r行的矩阵了，对SVD来说也是一样的，我们对SVD分解的式子两边乘以U的转置U'





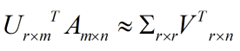
这样我们就得到了对行进行压缩的式子。可以看出，其实PCA几乎可以说是对SVD的一个包装，如果我们实现了SVD，那也就实现了PCA了，而且更好的地方是，有了SVD，我们就可以得到两个方向的PCA，如果我们对A’A进行特征值的分解，只能得到一个方向的PCA。

7.SVD与广义逆矩阵

在认识矩阵的广义逆之前，先来回顾一下方阵的逆。

对于一个

的方阵

，如果存在一个矩阵

，使得

，那么方阵

的逆为

。

那么对于非方阵来说情况又是怎样的？ 比如对于

的矩阵

，它的逆是怎样计算的？这就是我将要

讨论的广义逆矩阵。

矩阵的广义逆由Moore在1920年提出，后来在1955年经过Penrose发展得到如下定义

对任意

复数矩阵

，如果存在

的矩阵

，满足



则称

为

的一个Moore-Penrose逆，简称广义逆，记为

。并把上面四个方程叫做Moore-Penrose

方程，简称M-P方程。

由于M-P的四个方程都各有一定的解释，并且应用起来各有方便之处，所以出于不同的目的，常常考虑满足

部分方程的

，叫做弱逆，弱逆不唯一。为了引用方便，下面给出广义逆矩阵的定义

对于

的矩阵

，若存在

的矩阵

，满足M-P方程中的全部或者其中的一部分，则称

为


的广义逆矩阵。

实际上有结论：如果

满足M-P方程中的全部四个条件，那么得到的矩阵

是唯一的，如果只满足部分条件，

那么得到的矩阵

不唯一。也就是说一个矩阵

的Moore-Penrose逆

是唯一的。

而广义逆

的计算可以利用

的SVD分解得到，假设矩阵

的SVD分解为



那么，不难验证



有了广义逆矩阵

，那么就可以用来求解线性方程组

，假设现在已经知道了矩阵

的广义逆

，

如果矩阵

的秩是

，则其唯一解是

，如果秩小于

，则有无穷多组解，其中最小范数解仍然是


，通常我们关心的也就是这个解。



8. SVD与最小二乘法

最常见的最小二乘问题是线性最小二乘问题。比如在三维空间有如下四个点



现在用一个方程

来拟合这四个点，这就是典型的线性最小二乘问题。

接下来可以列出超定方程组，如下



那么，进一步得到



接下来用一个定理求最小二乘解，定理内容如下

如上述超定系数方程组，一般情况下它是没有解的，但是我们可以让

尽可能地小。解下面的方程

可以求得方程的最小二乘解。



这样最小二乘解又变成了解线性方程组问题，可以先用SVD来求出广义逆矩阵，然后解出

。最终求得解为



9. SVD与数据压缩

SVD在数据压缩方面有广泛的应用，比如图片压缩。我们知道电脑上的图像都是由一个一个像素点构成的，

所以存储一张1000*622的图片，实际上是存储一个1000*622的矩阵，即一共622000个元素，这是一个

很大的矩阵，实际上可以用奇异值分解并通过低阶近似的思想对图片进行压缩，但这是一种有损压缩，不

过不影响图片的大致效果，之后压缩为原来的四分之一大小。

链接：http://cos.name/2014/02/svd-and-image-compression/

又比如在自然语言处理中，最常见的两个问题是将文本按主题归类和将词汇表中的字词按近义词归类，这

两个问题都可以用SVD完美一次性地解决。首先，用一个大矩阵

来描述成千上万篇文章和上百万词的关

联性，在这个矩阵中，每一行代表一篇文章，每一列对应一个词。如果有

个词，

篇文章，那么就是如

下

的矩阵



其中第

行第

列的元素

，是字典中第

个词在第

篇文章中出现的加权词频，比如用词的TF-IDF值。

这个矩阵可能会很大，如果进行奇异值分解后，上述的两种分类也就完成了，而且存储空间也会减少很多。

10. SVD与LSA以及LSI

潜在语义分析（Latent Semantic Analysis）

简称LSA，是一种用于自动地实现知识提取和表示的

理论和方法，它通过对大量文本集进行统计分析，从中提取出词语的上下文使用含义。在技术上，它同向

量空间模型类似，都是采用空间向量表示文本，但通过SVD分解等处理消除了同义词，多义词的影响，提

高了后续处理的精度。

关于潜在语义分析的论文，可以百度：潜在语义分析理论及其应用。

潜在语义索引（Latent Semantic Indexing）

与PCA不太一样，至少不是实现了SVD就可以直接用的，不过LSI也是一个严重依赖于SVD的算法，之前吴军老师在矩阵计算与文本处理中的分类问题中谈到：

“三个矩阵有非常清楚的物理含义。第一个矩阵X中的每一行表示意思相关的一类词，其中的每个非零元素表示这类词中每个词的重要性（或者说相关性），数值越大越相关。最后一个矩阵Y中的每一列表示同一主题一类文章，其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵则表示类词和文章雷之间的相关性。因此，我们只要对关联矩阵A进行一次奇异值分解，w
我们就可以同时完成了近义词分类和文章的分类。（同时得到每类文章和每类词的相关性）。”

上面这段话可能不太容易理解，不过这就是LSI的精髓内容，我下面举一个例子来说明一下，下面的例子来自LSA tutorial，具体的网址我将在最后的引用中给出：





这就是一个矩阵，不过不太一样的是，这里的一行表示一个词在哪些title中出现了（一行就是之前说的一维feature），一列表示一个title中有哪些词，（这个矩阵其实是我们之前说的那种一行是一个sample的形式的一种转置，这个会使得我们的左右奇异向量的意义产生变化，但是不会影响我们计算的过程）。比如说T1这个title中就有guide、investing、market、stock四个词，各出现了一次，我们将这个矩阵进行SVD，得到下面的矩阵：





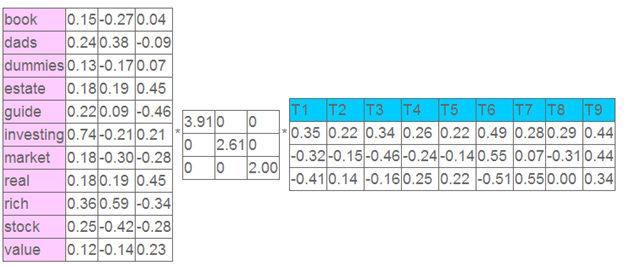
左奇异向量表示词的一些特性，右奇异向量表示文档的一些特性，中间的奇异值矩阵表示左奇异向量的一行与右奇异向量的一列的重要程序，数字越大越重要。

继续看这个矩阵还可以发现一些有意思的东西，首先，左奇异向量的第一列表示每一个词的出现频繁程度，虽然不是线性的，但是可以认为是一个大概的描述，比如book是0.15对应文档中出现的2次，investing是0.74对应了文档中出现了9次，rich是0.36对应文档中出现了3次；

其次，右奇异向量中一的第一行表示每一篇文档中的出现词的个数的近似，比如说，T6是0.49，出现了5个词，T2是0.22，出现了2个词。

然后我们反过头来看，我们可以将左奇异向量和右奇异向量都取后2维（之前是3维的矩阵），投影到一个平面上，可以得到：





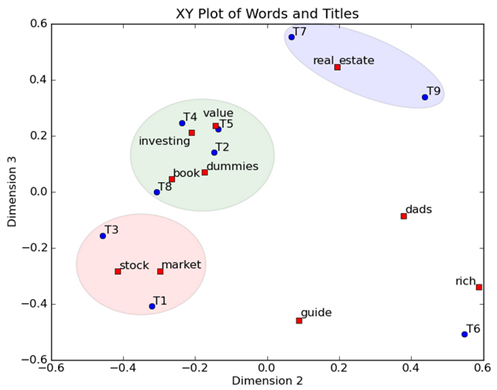
在图上，每一个红色的点，都表示一个词，每一个蓝色的点，都表示一篇文档，这样我们可以对这些词和文档进行聚类，比如说stock 和 market可以放在一类，因为他们老是出现在一起，real和estate可以放在一类，dads，guide这种词就看起来有点孤立了，我们就不对他们进行合并了。按这样聚类出现的效果，可以提取文档集合中的近义词，这样当用户检索文档的时候，是用语义级别（近义词集合）去检索了，而不是之前的词的级别。这样一减少我们的检索、存储量，因为这样压缩的文档集合和PCA是异曲同工的，二可以提高我们的用户体验，用户输入一个词，我们可以在这个词的近义词的集合中去找，这是传统的索引无法做到的。

转自
http://blog.csdn.net/bitcarmanlee/article/details/52068118 http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html http://blog.csdn.net/acdreamers/article/details/44656963