三、梯度下降与反向传播(含过程推导及证明)
2017-08-09 21:47
645 查看
本博客主要内容为图书《神经网络与深度学习》和National Taiwan University (NTU)林轩田老师的《Machine Learning》的学习笔记,因此在全文中对它们多次引用。初出茅庐,学艺不精,有不足之处还望大家不吝赐教。
C(w,b)=\frac1{2n}\sum_x||y(x)-a||^2\tag{1}\label{1}
公式里面的 w 表示所有的权重的集合, b 表示所有偏置的集合, n 是训练数据的个数, a 代表 x 作为输入时输出层的向量,求和针对所有的训练输入 x 。显而易见,输出 a 取决于 w 和 b ,但是 为了保持公式的简洁性,这里没有明确指出这种依赖性。称 C(w,b) 为二次代价函数,有时也称它为平方误差(MSE)。
在这里我们不增大正确输出的数量,而是去最小化一个像平方代价类似的间接评估,其主要目的在于提高分类器的准确率。 因为在神经网络中,被正确分类的图像的数量关于权重、偏置的函数并不是一 个平滑的函数。大多数情况下,对权重和偏置做出的微小变动并不会影响被正确分类的图像的数量,这会导致我们很难去刻画如何去优化权重和偏置才能得到更好的结果。一个类似平 方代价的平滑代价函数能够更好地指导我们如何去改变权重和偏置来达到更好的效果。
定义完代价函数后我们需要做的就是通过某一种算法调整函数的权重和偏置使得代价函数尽可能的小,因此下面介绍两种常用的方法。
在介绍梯度下降法的时候,首先忽略神经网络的结构,假设其为具有很多变量的函数,而我们的目的就是求解出这样的函数的最小值。当对自变量做较小的改变的时候
ΔC≈∇C⋅Δv(2)
其中 Δv=(Δv1, ……, Δvm) 表示自变量的变化量,∇C=(∂C∂v1, ……∂C∂vm) 表示梯度向量,ΔC 表示函数的变化量。假设我们取Δv=−ηΔC,这里的 η 是一个很小的正数,我们称之为学习率(Learning Rate),将 Δv 带入(2)可以得到
ΔC≈−η∇C⋅2(3)
因此保证ΔC≤0,使得C一直在下降,不会再增加。因此梯度下降算法工作的方式就是重复计算梯度∇C,然后沿着梯度的反方向运动, 即沿着山谷的斜坡下降。可以看作是一种通过在 C 下降最快的方向上做微小变化来使得 C 立即下降的方法。
为了使我们的梯度下降法能够正确地工作,我们需要选择足够小的学习速率 η 使得等式(2)能得到很好的近似。与此同时,我们也不能把 η 设得过小,因为如果 η 过小,那么梯度下降算法就会变得异常缓慢。在真正的实现中, η 通常是变化的,从而方程(2)能保持很好地近似度同时保证算法不会太慢;另外梯度下降法并不总是有效的,存在几种情况能导致错误的发生, 使得我们无法从梯度得到函数的全局最小值,这两个方面的内容会在后面的章节中讨论。
在神经网络中使用梯度下降法去寻找权重 w 和偏置 b 减小(2)中的代价函数,具体表现是
⎧⎩⎨⎪⎪wk→w′k=wk−η∂C∂wkbl→b′l=bl−η∂C∂bl(4)
C=1n∑xCx(5)
对(5)两侧同时求梯度可得
∇C=1n∑x∇Cx(6)
为了计算梯度,需要为每个样本 x 单独地计算梯度值 ∇C ,然后再求平均值。当训练输⼊的数量过⼤时会花费很⻓时间,这样会使学习变得相当缓慢。因此可以采用做随机梯度下降(SGD)的算法加速学习。
随机梯度下降通过随机选取⼩量的m个训练数据,并将它们标记为X1, X2, ……, Xm并把它们称为⼀个⼩批量数据(mini-batch)。假设样本数量 m ⾜够⼤,我们期望 ∇CXj 的平均值⼤致相等于整个 ∇C 的平均值,即
∑mj=1∇CXjm≈∑x∇Cxn=∇C(7)
因此可以采用随机梯度估计整体的梯度。假设 wk 和 bl 表⽰我们神经⽹络中权重和偏置, 随即梯度下降通过随机地选取并训练输⼊的⼩批量数据来⼯作
⎧⎩⎨⎪⎪⎪⎪wk→w′k=wk−ηm∑j∂CXj∂wkbl→b′l=bl−ηm∑j∂CXj∂bl(8)
其中两个求和符号是在当前⼩批量数据中的所有训练样本Xj上进⾏的。然后我们再挑选另⼀随 机选定的⼩批量数据去训练。直到我们⽤完了所有的训练输⼊,这被称为完成了⼀个训练迭代期(epoch),然后我们就会开始⼀个新的训练迭代期。
在⽅程(1)中,我们通过因⼦ 1n 来改变整个代价函数的⼤⼩。⼈们有时候忽略 1n 直接取单个训练样本的代价总和,⽽不是取平均值。这对我们不能提前知道训练数据数量的情况下特别有效。例如,这可能发⽣在有更多的训练数据是实时产⽣的情况下。同样,⼩批量数据的更新规则(8)有时也会舍弃前⾯的 1m 。
第一条假设
代价函数能够被写成C=1n∑xCx的形式,其中Cx是每个独立训练样本 的代价函数。
原因:反向传播实际上是对单个训练数据计算偏导数∂Cx∂w和∂Cx∂b。然后通过对所有训练样本求平均值获得∂C∂w和∂C∂b。
第二条假设
它可以写成关于神经网络输出结果的函数,或者理解成写成关于参数 w 和 b 的参数。
∂C∂w=1n∑x∂Cx∂w(9)
由此可以看出,只需要对计算出每一个数据的导数再相加就可以了,因此在求解的过程中只考虑其中的一项。根据链式法则可以知道
∂C∂w=∂z∂w∂C∂z=∂z∂w∂a∂z∂C∂a(10)
考虑第一项 ∂z∂w ,取其中某一个神经元的权值输入对其权重的导数为例,求导过程如图1所示
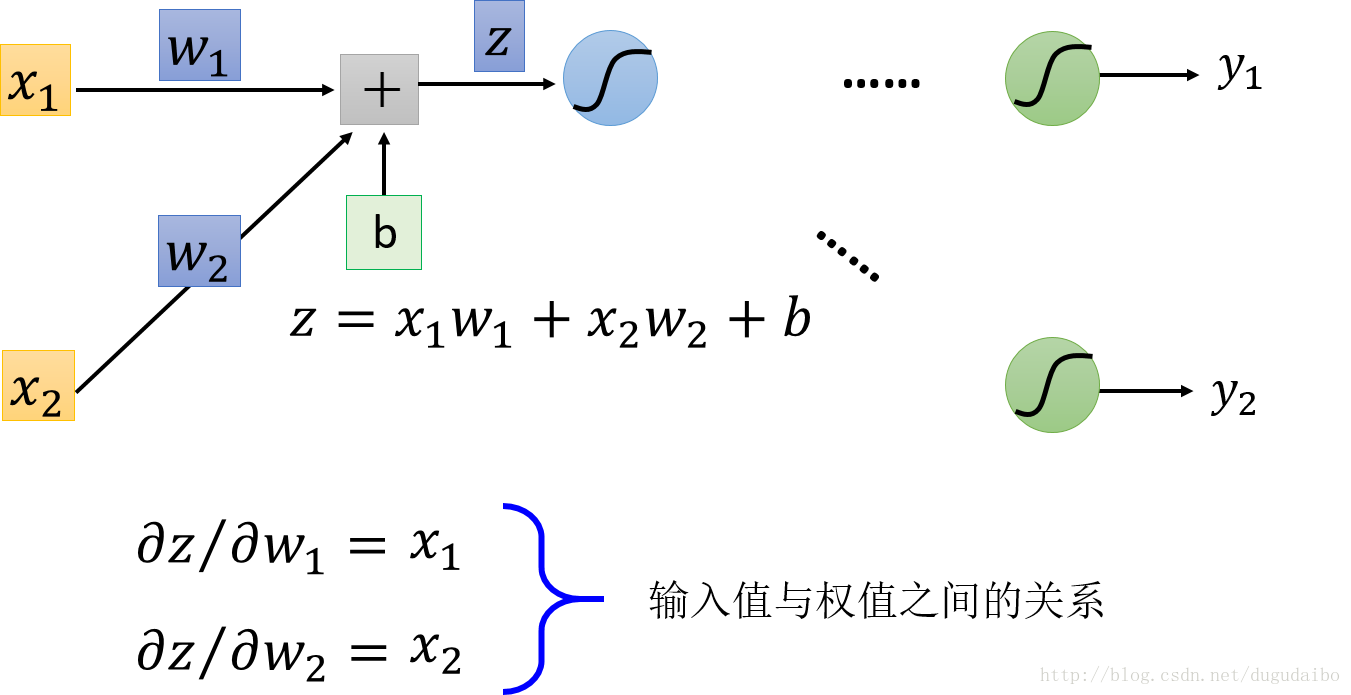
图1. 输入值与导数之间的关系
由此我们可以看到某一个加权输入 z 对于某一个权值 wj 的偏微分就是这个权值对应的输入值。因此只要知道某一层神经元的激活值 al−1 就可以得到第 l 层的 zl 对于第 l 层的 wl 的偏微分值, ∂z∂w 的快速求法将在下一节的前向传播中具体介绍。
考虑第二项 ∂a∂z ,因为对于某一种确定的激活函数肯定可以提前知道该激活函数 σ(z) 的导数的表达式,因此只需要将在前向传播计算过程中保存的 z 的值带入即可。
考虑最后一项 ∂C∂a ,假设此时的神经网络的结构如图2所示
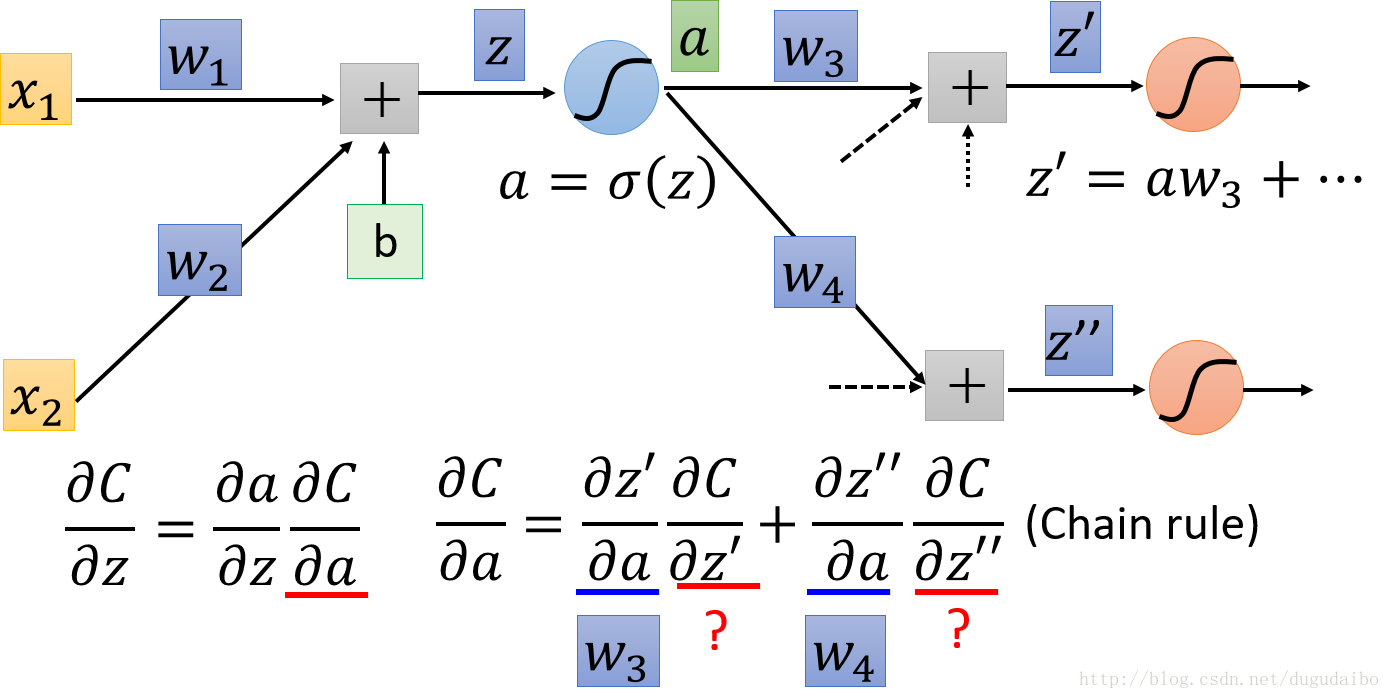
图2. 链式法则求解 ∂C∂a
从图2可以看出 ∂C∂a 的值主要受到 w3 和 w4 两条路径的影响,因此可以将 ∂C∂a 经过链式法则分解为图2的形式,转化为求解下一层的 ∂C∂z′与∂C∂z′‘ ,如果假定这两个值已经知道,则 ∂C∂a 的值可以通过如图3的方式求得
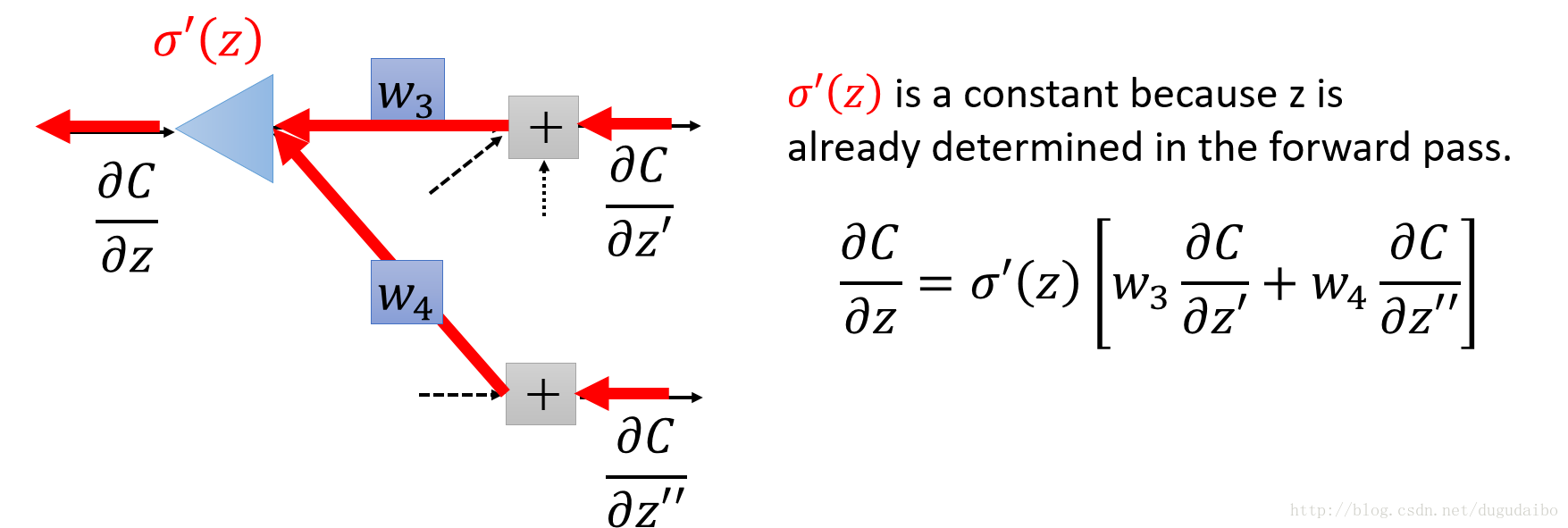
图3. 反向传播计算示意图
因此可以首先求出最后一层的 ∂C∂a L ,通过反向传播算法求解出待解的 ∂C∂a 。
a lj=σ(∑kw ljka l−1j+b lj)(11)
注意这里的求和只是针对第 l−1 层的所有神经元第 k 。将其表示为矩阵的形式为
a lj=σ⎛⎝⎜[w lj1…w ljk]⋅⎡⎣⎢a l−11…a l−1k⎤⎦⎥+b lj⎞⎠⎟(12)
前向传播是一种基于矩阵的快速计算神经网络输出的方法。为了实现这个目的,我们在图4 的神经网络中定义了这些矩阵及向量。
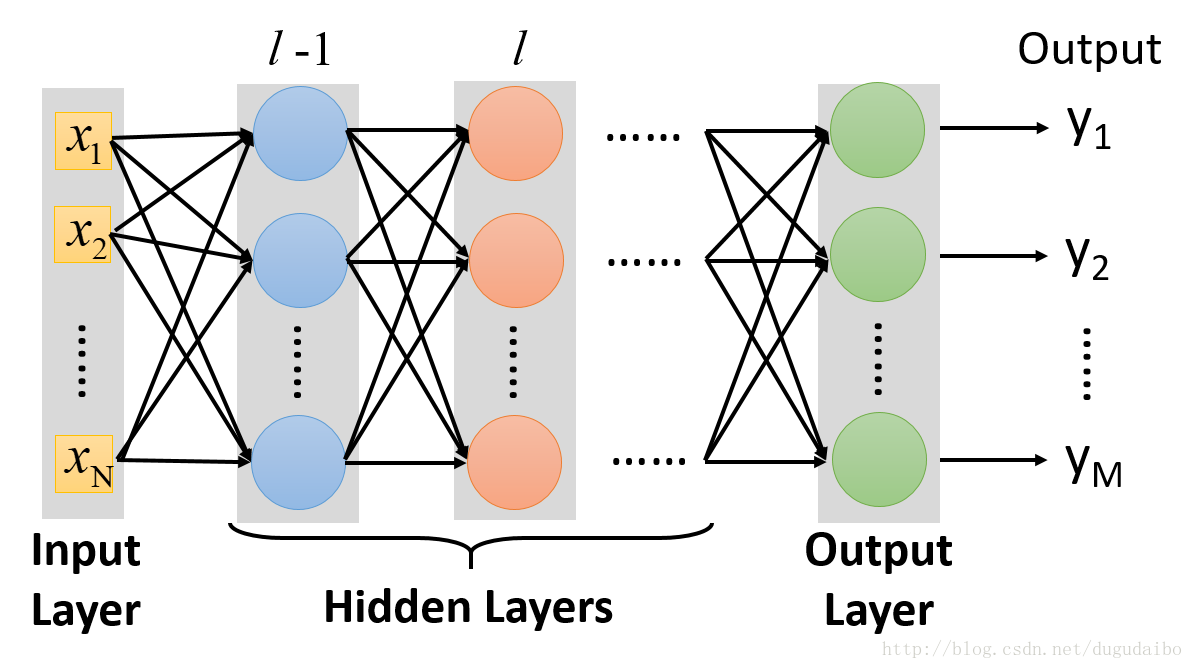
图4.神经网络结构示意图
权重矩阵 w l
权重矩阵 w l 的每一项就是连接到第 l 层神经元的权重,即 w l 中第 j 行第 k 列的元素就是 w ljk 。因此权重矩阵 w l 的行数是第 l 层神经元的个数,列数是第 l−1 层神经元的个数(这个是十分重要的,因为在后期的编程中会用到这个知识点)。
偏移向量 b l
偏移向量 b l 的每一项对应第 l 层中的一个神经元 b lj 的值。
激活向量 a l
激活向量 a l 的每一项对应第 l 层中的一个神经元 a lj 的值。
通过上述对于矩阵及向量的定义可以将每一层的激活函数值表示为如下的形式
a l=σ⎛⎝⎜⎜⎜⎜⎡⎣⎢⎢⎢⎢⎢w l11w l21…w lj1w l12w l22…w lj2…………w l1kw l2k…w ljk⎤⎦⎥⎥⎥⎥⎥⋅⎡⎣⎢⎢⎢⎢a l−11a l−12…a l−1k⎤⎦⎥⎥⎥⎥+⎡⎣⎢⎢⎢⎢b l−11b l−12…b l−1k⎤⎦⎥⎥⎥⎥⎞⎠⎟⎟⎟⎟=σ(∑w la l−1+b l)(13)
我们仅仅将权重矩阵作用于上一层的激活值,然后加上偏置向量,最后用 函数作用于这个结果,就得到了本层的激活函数值。(注意在计算的也要存储z l=∑w la l−1+b l的值)
s⨀t=[12]⨀[34]=[1×32×4]=[38]
这种对应元素相乘有时被称为Hadamard积(Hadamard product)或Schur积(Schur product)。我们将称它为Hadamard积。优秀的矩阵库通常会提供Hadamard积的快速实现, 这在实现反向传播时将会有用。
Hadamard积所实现的功能同样可以通过矩阵相乘得到。讲左侧的向量 s 写成一个方阵的形式,其中对角线元素是 s 中的值,而非对角线元素都是0,将这个对角矩阵记为 ∑′(s),则上式可以写为
s⨀t=∑′(s) t
但是这种矩阵表示的方法在数值计算的过程中明显慢于Hadamard积,因此后文均采用Hadamard积的形式。
δL=∇aC⨀σ′(zL)
证明:取输出层的某一个神经元 aLj 为例,应用链式法则可以得到如下的形式
δLj=∂C∂zLj=∑k∂aLk∂zLj∂C∂aLk(14)
因为在应用链式法则的过程中考虑到所有可能影响到 C 的路径,因此这里的求和是对于输出层的所有神经元 k 而言的。但是通过分析我们可以知道,对于第一项 ∂aLk∂zLj 只有当 j=k 的时候才能取到非零值,因此上式可以化简为如下的形式
δLj=∂aLj∂zLj∂C∂aLj(15)
其中取σ′(zLj)=∂aLj∂zLj,即可得到
δLj=∂C∂aLjσ′(zLj)(16)
如果将输出层的所有神经元写成向量的形式,将 [∂C∂aL1,…,∂C∂aL1]T记为 ∇aC ,则可以得到上述的形式。
δ l=((w l+1)Tδ l+1)⨀σ′(z l)
证明:应用链式法则可以得到
δlj=∂C∂zlj=∑k∂C∂zl+1k∂zl+1k∂zlj=∑k∂zl+1k∂zljδl+1j(17)
为了计算最后一行将 zk+1 展开可得
zl+1k=∑jwl+1kjalj+bl+1k=∑jwl+1kjσ(zlj)+bl+1k(18)
在此应该注意的是 wl+1kj 下标,根据下标可以知道在这里第 l 层神经元具有的神经元的个数是 j 个,而第 l+1 层神经元具有的神经元的个数是 k 个。对上式进行求导可得
∂zl+1k∂zlj=wl+1kjσ′(zlj)(19)
带回到式(17)可以得到
δkj=∑kwl+1kjδl+1kσ′(zlj)(20)
将上述的表达式写成矩阵的形式为
δkj=[wl+11j,…,wl+1kj]⎡⎣⎢⎢δl+11…δl+1k⎤⎦⎥⎥σ′(zlj)(21)
在上面的表达式中 w 与 δ 所代表的矩阵的维数分别是 1×k 和 k×1 ,但是由 wl+1kj 构成的矩阵 wl+1 的维数是 k×j 的,因此在用矩阵表示时候需要对 wl+1 进行转置,即如下所示
δ l=((w l+1)Tδ l+1)⨀σ′(z l)(22)
∂C∂blj=δj l
证明:
∂C∂blj=∂C∂zlj∂zlj∂blj=δj l
∂C∂wjkl=al−1kδlj
证明:
∂C∂wjkl=∂C∂zlj∂zlj∂wjkl=δj lal−1k
分析上面的四个基本等式可以得到两条明显的结论
结论1
如果输入神经元是低激活量的,或者输出神经元已经饱和 (高激活量或低激活量),那么权重就会学习得缓慢。
结论2
这四个基本的等式在使用任何激活函数的情况下都是成立的,不仅仅是标准的sigmoid函数,这是因为证明的过程并没有使用sigmoid函数的属性。所以我们可以利用这些等式来设计激活函数,使这些函数具有特殊目的的学习特性。
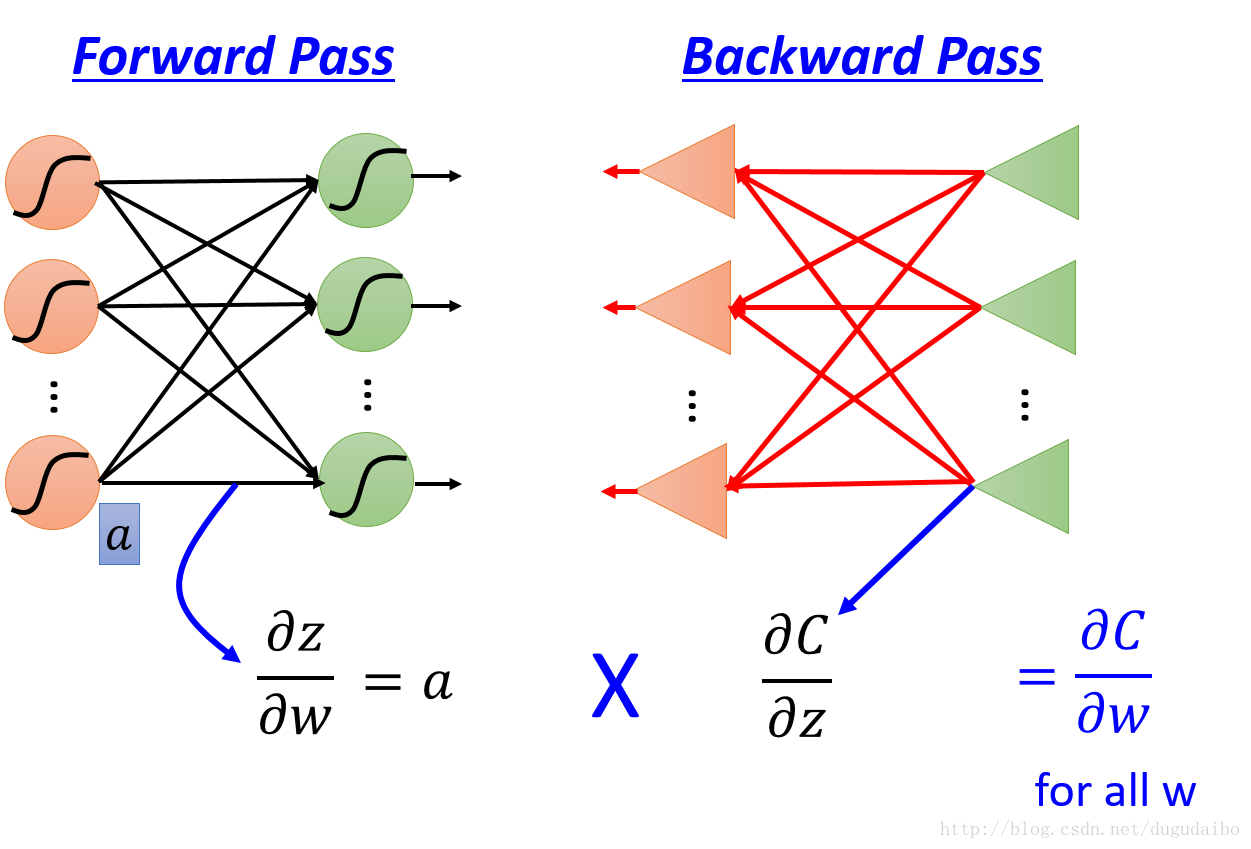
图5. 反向传播算法整体描述
具体分为以下5个步骤
1. 输入 x
计算输入层相应的激活函数值a1 。
2. 正向传播
对每个 l=2,3,...,L,计算 zl=wlal−1+bl 和 al=σ(zl) 。
3. 输出误差 δL
计算向量 δL=∇aC⨀σ′(zL)
4. 将误差反向传播
对每个 l=L−1,L−2,...,2 计算δ l=((w l+1)Tδ l+1)⨀σ′(z l)
5. 输出
代价函数的梯度为 ∂C∂wjkl=al−1kδlj 和 ∂C∂blj=δj l
2. 对每个训练样本x,相应的输入激活值记为 ax,l 并执行以下步骤:
2.1 正向传播:对每个 l=2,3,...,L,计算 z x,l=w lax,l−1+b l 和 a x,l=σ(zx,l)
2.2 输出误差 δ x,L:计算向量 δ x,L=∇aC⨀σ′(z x,L)
2.3 将误差反向传播:对每个 l=L−1,L−2,...,2 计算δ x,l=((w l+1)Tδ x,l+1)⨀σ‘(z x,l)
3. 梯度下降:对每个 l=L−1,L−2,...,2 分别根据法则
w l→w l−ηm∑xax,l−1kδx,lj 和 b l→b l−ηm∑xδx,lj 更新权重和偏移值,其中的 m 是一个mini-batch中样本的个数。
反向传播的优点在于它仅利用一次前向传播就可以同时计算出所有的偏导 ∂C∂wj,随后也仅需要一次反向传播。
缺点
在80年代后期,人们终于 触及到了性能瓶颈,在利用反向传播算法来训练深度神经网络(即具有很多隐含层的网络)时尤为明显。
1 代价函数
用 x 定义训练集的输入数据,用 y 定义训练集输入数据的标签。现在我们需要一个算法能让我们找到合适的权重 w 和偏置 b,从而对所有的训练输入为 x 的输出都近似于 y 。 为了衡量我们当前取得的结果距离目标结果的好坏程度,我们定义一个代价函数C(w,b)=\frac1{2n}\sum_x||y(x)-a||^2\tag{1}\label{1}
公式里面的 w 表示所有的权重的集合, b 表示所有偏置的集合, n 是训练数据的个数, a 代表 x 作为输入时输出层的向量,求和针对所有的训练输入 x 。显而易见,输出 a 取决于 w 和 b ,但是 为了保持公式的简洁性,这里没有明确指出这种依赖性。称 C(w,b) 为二次代价函数,有时也称它为平方误差(MSE)。
在这里我们不增大正确输出的数量,而是去最小化一个像平方代价类似的间接评估,其主要目的在于提高分类器的准确率。 因为在神经网络中,被正确分类的图像的数量关于权重、偏置的函数并不是一 个平滑的函数。大多数情况下,对权重和偏置做出的微小变动并不会影响被正确分类的图像的数量,这会导致我们很难去刻画如何去优化权重和偏置才能得到更好的结果。一个类似平 方代价的平滑代价函数能够更好地指导我们如何去改变权重和偏置来达到更好的效果。
定义完代价函数后我们需要做的就是通过某一种算法调整函数的权重和偏置使得代价函数尽可能的小,因此下面介绍两种常用的方法。
2 参数更新方法
2.1 梯度下降方法
取目标函数 C(v) ,其中 v =v1, ……vm, ,用 v 去代表 w 和 b 以强调它可能是任意的函数。在求解目标函数最小值的过程中理论上可以采用两种方法进行计算:一种解决方法就是用数值计算的方法去计算出它的最小值,但是这种方法需要求偏导数,然而在参数量巨大的神经网络中这是很难完成的一件事情;另一种方法是采用梯度下降的方法,计算较为简便。在介绍梯度下降法的时候,首先忽略神经网络的结构,假设其为具有很多变量的函数,而我们的目的就是求解出这样的函数的最小值。当对自变量做较小的改变的时候
ΔC≈∇C⋅Δv(2)
其中 Δv=(Δv1, ……, Δvm) 表示自变量的变化量,∇C=(∂C∂v1, ……∂C∂vm) 表示梯度向量,ΔC 表示函数的变化量。假设我们取Δv=−ηΔC,这里的 η 是一个很小的正数,我们称之为学习率(Learning Rate),将 Δv 带入(2)可以得到
ΔC≈−η∇C⋅2(3)
因此保证ΔC≤0,使得C一直在下降,不会再增加。因此梯度下降算法工作的方式就是重复计算梯度∇C,然后沿着梯度的反方向运动, 即沿着山谷的斜坡下降。可以看作是一种通过在 C 下降最快的方向上做微小变化来使得 C 立即下降的方法。
为了使我们的梯度下降法能够正确地工作,我们需要选择足够小的学习速率 η 使得等式(2)能得到很好的近似。与此同时,我们也不能把 η 设得过小,因为如果 η 过小,那么梯度下降算法就会变得异常缓慢。在真正的实现中, η 通常是变化的,从而方程(2)能保持很好地近似度同时保证算法不会太慢;另外梯度下降法并不总是有效的,存在几种情况能导致错误的发生, 使得我们无法从梯度得到函数的全局最小值,这两个方面的内容会在后面的章节中讨论。
在神经网络中使用梯度下降法去寻找权重 w 和偏置 b 减小(2)中的代价函数,具体表现是
⎧⎩⎨⎪⎪wk→w′k=wk−η∂C∂wkbl→b′l=bl−η∂C∂bl(4)
2.2 随机梯度下降法
根据(1)可知,代价函数可以写成如下的形式C=1n∑xCx(5)
对(5)两侧同时求梯度可得
∇C=1n∑x∇Cx(6)
为了计算梯度,需要为每个样本 x 单独地计算梯度值 ∇C ,然后再求平均值。当训练输⼊的数量过⼤时会花费很⻓时间,这样会使学习变得相当缓慢。因此可以采用做随机梯度下降(SGD)的算法加速学习。
随机梯度下降通过随机选取⼩量的m个训练数据,并将它们标记为X1, X2, ……, Xm并把它们称为⼀个⼩批量数据(mini-batch)。假设样本数量 m ⾜够⼤,我们期望 ∇CXj 的平均值⼤致相等于整个 ∇C 的平均值,即
∑mj=1∇CXjm≈∑x∇Cxn=∇C(7)
因此可以采用随机梯度估计整体的梯度。假设 wk 和 bl 表⽰我们神经⽹络中权重和偏置, 随即梯度下降通过随机地选取并训练输⼊的⼩批量数据来⼯作
⎧⎩⎨⎪⎪⎪⎪wk→w′k=wk−ηm∑j∂CXj∂wkbl→b′l=bl−ηm∑j∂CXj∂bl(8)
其中两个求和符号是在当前⼩批量数据中的所有训练样本Xj上进⾏的。然后我们再挑选另⼀随 机选定的⼩批量数据去训练。直到我们⽤完了所有的训练输⼊,这被称为完成了⼀个训练迭代期(epoch),然后我们就会开始⼀个新的训练迭代期。
在⽅程(1)中,我们通过因⼦ 1n 来改变整个代价函数的⼤⼩。⼈们有时候忽略 1n 直接取单个训练样本的代价总和,⽽不是取平均值。这对我们不能提前知道训练数据数量的情况下特别有效。例如,这可能发⽣在有更多的训练数据是实时产⽣的情况下。同样,⼩批量数据的更新规则(8)有时也会舍弃前⾯的 1m 。
3. 反向传播算法
在上一节中我们学习了神经网络是如何利用梯度下降算法来学习权重(weights)和偏置 (biases)的,在这一节将介绍一个快速计算梯度的算法,即反向传播算法(backpropagation)。3.1 损失函数的两个假设
为了使反向传播工作,需要对代价函数的结构做两个主要假设。第一条假设
代价函数能够被写成C=1n∑xCx的形式,其中Cx是每个独立训练样本 的代价函数。
原因:反向传播实际上是对单个训练数据计算偏导数∂Cx∂w和∂Cx∂b。然后通过对所有训练样本求平均值获得∂C∂w和∂C∂b。
第二条假设
它可以写成关于神经网络输出结果的函数,或者理解成写成关于参数 w 和 b 的参数。
3.2 BP算法的总体思路
再利用梯度下降法求梯度时,根据损失函数的第一条假设,先只对目标函数(5)中的 w 求导可得∂C∂w=1n∑x∂Cx∂w(9)
由此可以看出,只需要对计算出每一个数据的导数再相加就可以了,因此在求解的过程中只考虑其中的一项。根据链式法则可以知道
∂C∂w=∂z∂w∂C∂z=∂z∂w∂a∂z∂C∂a(10)
考虑第一项 ∂z∂w ,取其中某一个神经元的权值输入对其权重的导数为例,求导过程如图1所示

图1. 输入值与导数之间的关系
由此我们可以看到某一个加权输入 z 对于某一个权值 wj 的偏微分就是这个权值对应的输入值。因此只要知道某一层神经元的激活值 al−1 就可以得到第 l 层的 zl 对于第 l 层的 wl 的偏微分值, ∂z∂w 的快速求法将在下一节的前向传播中具体介绍。
考虑第二项 ∂a∂z ,因为对于某一种确定的激活函数肯定可以提前知道该激活函数 σ(z) 的导数的表达式,因此只需要将在前向传播计算过程中保存的 z 的值带入即可。
考虑最后一项 ∂C∂a ,假设此时的神经网络的结构如图2所示

图2. 链式法则求解 ∂C∂a
从图2可以看出 ∂C∂a 的值主要受到 w3 和 w4 两条路径的影响,因此可以将 ∂C∂a 经过链式法则分解为图2的形式,转化为求解下一层的 ∂C∂z′与∂C∂z′‘ ,如果假定这两个值已经知道,则 ∂C∂a 的值可以通过如图3的方式求得

图3. 反向传播计算示意图
因此可以首先求出最后一层的 ∂C∂a L ,通过反向传播算法求解出待解的 ∂C∂a 。
3.3 前向传播
在上一小节中已经得出结论,如果想求出∂z∂w 的值,只需要求出上一层神经元的激活值即可,其中第 l 层第 j 个神经元的激活值表示为如下的形式(因为只是讲述求解的思路,所以仅仅以 w 为例)a lj=σ(∑kw ljka l−1j+b lj)(11)
注意这里的求和只是针对第 l−1 层的所有神经元第 k 。将其表示为矩阵的形式为
a lj=σ⎛⎝⎜[w lj1…w ljk]⋅⎡⎣⎢a l−11…a l−1k⎤⎦⎥+b lj⎞⎠⎟(12)
前向传播是一种基于矩阵的快速计算神经网络输出的方法。为了实现这个目的,我们在图4 的神经网络中定义了这些矩阵及向量。

图4.神经网络结构示意图
权重矩阵 w l
权重矩阵 w l 的每一项就是连接到第 l 层神经元的权重,即 w l 中第 j 行第 k 列的元素就是 w ljk 。因此权重矩阵 w l 的行数是第 l 层神经元的个数,列数是第 l−1 层神经元的个数(这个是十分重要的,因为在后期的编程中会用到这个知识点)。
偏移向量 b l
偏移向量 b l 的每一项对应第 l 层中的一个神经元 b lj 的值。
激活向量 a l
激活向量 a l 的每一项对应第 l 层中的一个神经元 a lj 的值。
通过上述对于矩阵及向量的定义可以将每一层的激活函数值表示为如下的形式
a l=σ⎛⎝⎜⎜⎜⎜⎡⎣⎢⎢⎢⎢⎢w l11w l21…w lj1w l12w l22…w lj2…………w l1kw l2k…w ljk⎤⎦⎥⎥⎥⎥⎥⋅⎡⎣⎢⎢⎢⎢a l−11a l−12…a l−1k⎤⎦⎥⎥⎥⎥+⎡⎣⎢⎢⎢⎢b l−11b l−12…b l−1k⎤⎦⎥⎥⎥⎥⎞⎠⎟⎟⎟⎟=σ(∑w la l−1+b l)(13)
我们仅仅将权重矩阵作用于上一层的激活值,然后加上偏置向量,最后用 函数作用于这个结果,就得到了本层的激活函数值。(注意在计算的也要存储z l=∑w la l−1+b l的值)
3.4 反向传播
3.4.1 Hadamard积(s⨀t)
假设 s 和 t 是两个有相同维数的向量用 s⨀t 来表示两个向量的对应元素(elementwise)相乘。因此 s⨀t 的元素 (s⨀t) j=sj tj。例如,s⨀t=[12]⨀[34]=[1×32×4]=[38]
这种对应元素相乘有时被称为Hadamard积(Hadamard product)或Schur积(Schur product)。我们将称它为Hadamard积。优秀的矩阵库通常会提供Hadamard积的快速实现, 这在实现反向传播时将会有用。
Hadamard积所实现的功能同样可以通过矩阵相乘得到。讲左侧的向量 s 写成一个方阵的形式,其中对角线元素是 s 中的值,而非对角线元素都是0,将这个对角矩阵记为 ∑′(s),则上式可以写为
s⨀t=∑′(s) t
但是这种矩阵表示的方法在数值计算的过程中明显慢于Hadamard积,因此后文均采用Hadamard积的形式。
3.4.2 反向传播算法中的四个基本等式
通过上述的分析,梯度的求解可以归结为以下四个基本等式δL=∇aC⨀σ′(zL)
证明:取输出层的某一个神经元 aLj 为例,应用链式法则可以得到如下的形式
δLj=∂C∂zLj=∑k∂aLk∂zLj∂C∂aLk(14)
因为在应用链式法则的过程中考虑到所有可能影响到 C 的路径,因此这里的求和是对于输出层的所有神经元 k 而言的。但是通过分析我们可以知道,对于第一项 ∂aLk∂zLj 只有当 j=k 的时候才能取到非零值,因此上式可以化简为如下的形式
δLj=∂aLj∂zLj∂C∂aLj(15)
其中取σ′(zLj)=∂aLj∂zLj,即可得到
δLj=∂C∂aLjσ′(zLj)(16)
如果将输出层的所有神经元写成向量的形式,将 [∂C∂aL1,…,∂C∂aL1]T记为 ∇aC ,则可以得到上述的形式。
δ l=((w l+1)Tδ l+1)⨀σ′(z l)
证明:应用链式法则可以得到
δlj=∂C∂zlj=∑k∂C∂zl+1k∂zl+1k∂zlj=∑k∂zl+1k∂zljδl+1j(17)
为了计算最后一行将 zk+1 展开可得
zl+1k=∑jwl+1kjalj+bl+1k=∑jwl+1kjσ(zlj)+bl+1k(18)
在此应该注意的是 wl+1kj 下标,根据下标可以知道在这里第 l 层神经元具有的神经元的个数是 j 个,而第 l+1 层神经元具有的神经元的个数是 k 个。对上式进行求导可得
∂zl+1k∂zlj=wl+1kjσ′(zlj)(19)
带回到式(17)可以得到
δkj=∑kwl+1kjδl+1kσ′(zlj)(20)
将上述的表达式写成矩阵的形式为
δkj=[wl+11j,…,wl+1kj]⎡⎣⎢⎢δl+11…δl+1k⎤⎦⎥⎥σ′(zlj)(21)
在上面的表达式中 w 与 δ 所代表的矩阵的维数分别是 1×k 和 k×1 ,但是由 wl+1kj 构成的矩阵 wl+1 的维数是 k×j 的,因此在用矩阵表示时候需要对 wl+1 进行转置,即如下所示
δ l=((w l+1)Tδ l+1)⨀σ′(z l)(22)
∂C∂blj=δj l
证明:
∂C∂blj=∂C∂zlj∂zlj∂blj=δj l
∂C∂wjkl=al−1kδlj
证明:
∂C∂wjkl=∂C∂zlj∂zlj∂wjkl=δj lal−1k
分析上面的四个基本等式可以得到两条明显的结论
结论1
如果输入神经元是低激活量的,或者输出神经元已经饱和 (高激活量或低激活量),那么权重就会学习得缓慢。
结论2
这四个基本的等式在使用任何激活函数的情况下都是成立的,不仅仅是标准的sigmoid函数,这是因为证明的过程并没有使用sigmoid函数的属性。所以我们可以利用这些等式来设计激活函数,使这些函数具有特殊目的的学习特性。
3.5 反向传播算法整体描述
反向传播等式为我们提供了一个计算代价函数梯度的方法,如图5所示,计算某一层神经网络的梯度可以通过分别求前向传播与反向传播值相乘得到最后的结果。
图5. 反向传播算法整体描述
具体分为以下5个步骤
1. 输入 x
计算输入层相应的激活函数值a1 。
2. 正向传播
对每个 l=2,3,...,L,计算 zl=wlal−1+bl 和 al=σ(zl) 。
3. 输出误差 δL
计算向量 δL=∇aC⨀σ′(zL)
4. 将误差反向传播
对每个 l=L−1,L−2,...,2 计算δ l=((w l+1)Tδ l+1)⨀σ′(z l)
5. 输出
代价函数的梯度为 ∂C∂wjkl=al−1kδlj 和 ∂C∂blj=δj l
3.6 BP算法在随机梯度下降中的应用
1. 输入一组训练样本2. 对每个训练样本x,相应的输入激活值记为 ax,l 并执行以下步骤:
2.1 正向传播:对每个 l=2,3,...,L,计算 z x,l=w lax,l−1+b l 和 a x,l=σ(zx,l)
2.2 输出误差 δ x,L:计算向量 δ x,L=∇aC⨀σ′(z x,L)
2.3 将误差反向传播:对每个 l=L−1,L−2,...,2 计算δ x,l=((w l+1)Tδ x,l+1)⨀σ‘(z x,l)
3. 梯度下降:对每个 l=L−1,L−2,...,2 分别根据法则
w l→w l−ηm∑xax,l−1kδx,lj 和 b l→b l−ηm∑xδx,lj 更新权重和偏移值,其中的 m 是一个mini-batch中样本的个数。
3.7 BP算法的优缺点
优点反向传播的优点在于它仅利用一次前向传播就可以同时计算出所有的偏导 ∂C∂wj,随后也仅需要一次反向传播。
缺点
在80年代后期,人们终于 触及到了性能瓶颈,在利用反向传播算法来训练深度神经网络(即具有很多隐含层的网络)时尤为明显。
相关文章推荐
- BP神经网络,BP推导过程,反向传播算法,误差反向传播,梯度下降,权值阈值更新推导,隐含层权重更新公式
- 梯度下降法和误差反向传播推导
- 深度学习第三次课-梯度下降与反向传播
- DNN反向传播推导过程
- bp网络反向传播梯度下降修改权值
- 梯度下降和反向传播
- 神经网络之梯度下降与反向传播(上)
- 反向传播的工作过程以及公式推导
- 神经网络之梯度下降与反向传播(下)
- 【深度学习】梯度下降和反向传播
- 深度学习基础:反向传播即BP算法的推导过程
- DNN反向传播推导过程
- 反向传播与梯度下降的基本概念
- PyTorch: 梯度下降及反向传播
- 梯度下降法与反向传播
- 逻辑回归梯度下降法的推导过程
- 梯度下降法与反向传播
- 反向传播(Back propagation)算法推导具体过程
- 神经网络之梯度下降法和反向传播BP
- CNN中的梯度的求法和反向传播过程
