神经网络之卷积理解
2017-07-13 16:06
253 查看
卷积看了也使用了不少时间了,最近在知乎上如何理解深度学习中的deconvolution networks看到一个关于卷积的,感觉不错,因此有把那篇讲卷积的文章A guide to convolution arithmetic for deep learning看了一遍。
首先是卷积和反卷积的输入和输出形状(shape)大小,受到padding、strides和核的大小的影响。其计算如下:
注:其中o表示卷积操作输出结果,i表示卷积输入大小,k表示卷积核大小,p表示padding大小,s表示strides大小,o’, i’, k’, p’, s’则表示相应的反卷积操作大小. a 表示如果在卷积时移动步长(strides)不为1,且不能被strides整除,则其反卷积操作需要在输入i’的上边和右边补0,其大小为a,a = (i + 2k - p).
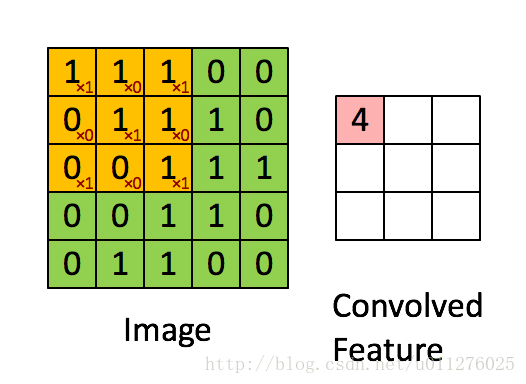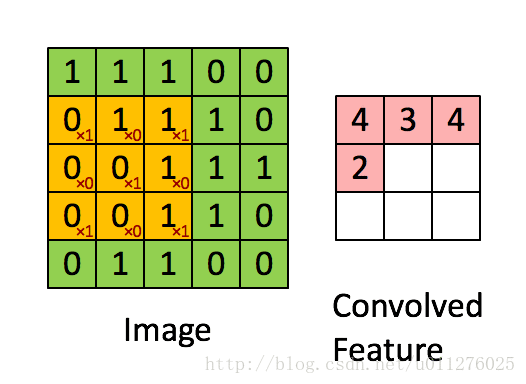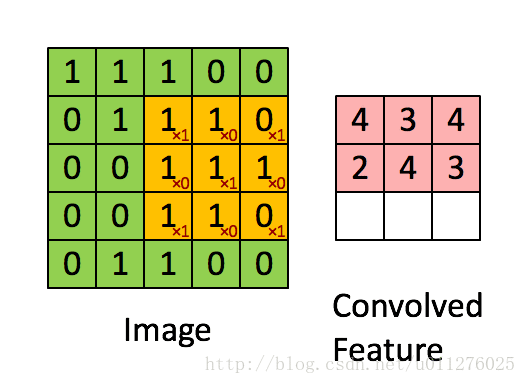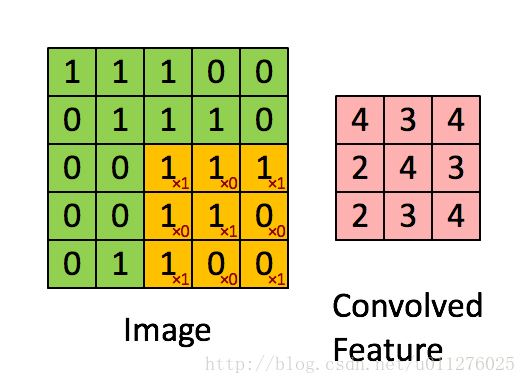
就是通过一个卷积核在图片像素中移动进行计算,同时,这种平移计算卷积的操作也可以看成矩阵操作,对于上面一个输入为5x5的输入,核为3x3的卷积来说(无padding且1 strides),把输入、卷积核和输出都展开为向量形式:
输入为25维的列向量 x
x=[11100...01100]
核扩充为9x25维的矩阵 C
C=⎡⎣⎢⎢⎢⎢w0,00...0w0,1w0,00w0,2w0,10w0,3w0,200w0,30000.........⎤⎦⎥⎥⎥⎥=⎡⎣⎢1...00010000000......⎤⎦⎥
输出为4维的行向量y=Cx
x=[434243234]
y=Cx
则对于单个xj有:
∂L∂xj=∑i∂L∂yi⋅∂yi∂xj=∑i∂L∂yi⋅Ci,j=∂L∂y⋅C∗,j=CT∗,j⋅∂L∂y
则对于x有:
∂L∂x=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢∂L∂x1∂L∂x2...∂L∂xn⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥= ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢CT∗,1⋅∂L∂yCT∗,2⋅∂L∂y...CT∗,n⋅∂L∂y⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥=CT⋅∂L∂y
根据上面矩阵表示卷积的前向和反向传播的过程,其反卷积的操作就非常简单了,只需要对C进行转置就好了,C′=CT.
即:
x=CTy
∂L∂x=C⋅∂L∂y
因此,在反卷积中不需要改变核的大小。

输出大小为:o=(i−k)+1
解释: 只看一次重做到右的滑动,一共滑动i−k次,在加上本身初始所在的位置,所以输出为(i−k)+1。
k’ = k
s’ = s
p’ = k-1
解释:k和s在反卷积中不改变,卷积操作使得输出减小了k−1, 则反卷积操作需要使输出还原到原大小,即输出增加k−1, 得:i′+(k−1)=(i′+2p′−k′)+1 –> p′=k−1.
其过程如下所示:
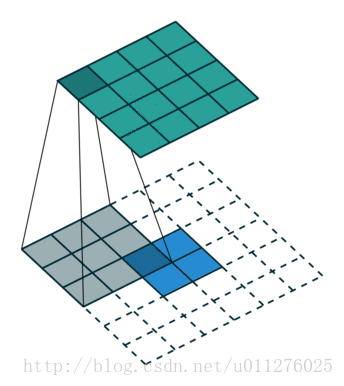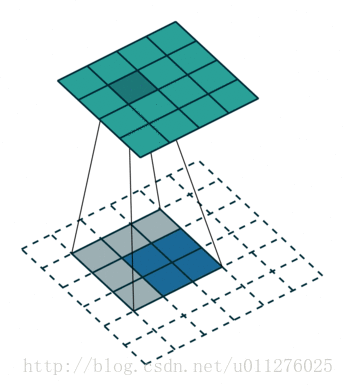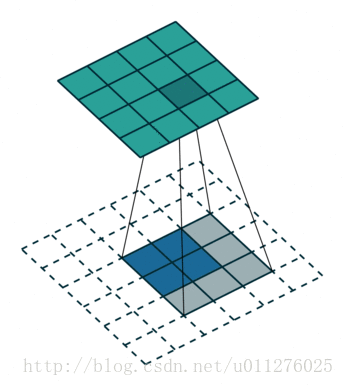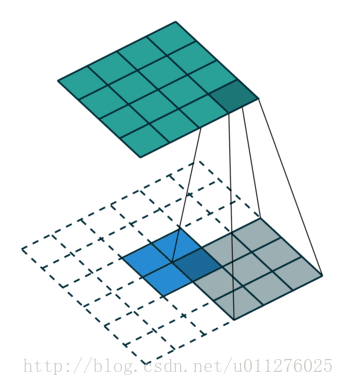
输出大小为:o′=i′+(k−1)
解释:o′=(i′+2p′−k′)+1=i′+(k−1)

输出大小为:o=(i−k)+2p+1
**解释:**padding在矩阵周围增加了p个单位的0,因此其输入大小增加为i+2p, 即,o=(i+2p−k)+1
解释:同理,卷积操作减少了k−2p−1, 在反卷积中需要增加回来,则,i′+(k−2p−1)=(i′+2p;−k′)+1 –> p=k−p−1.
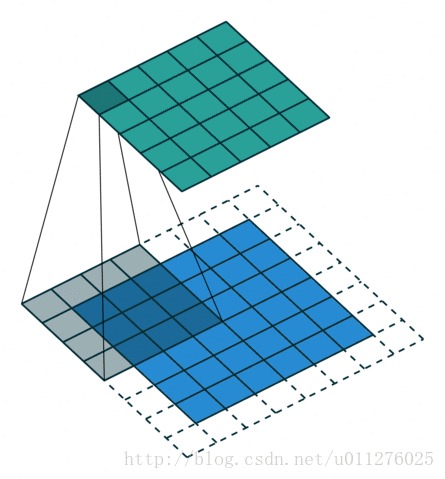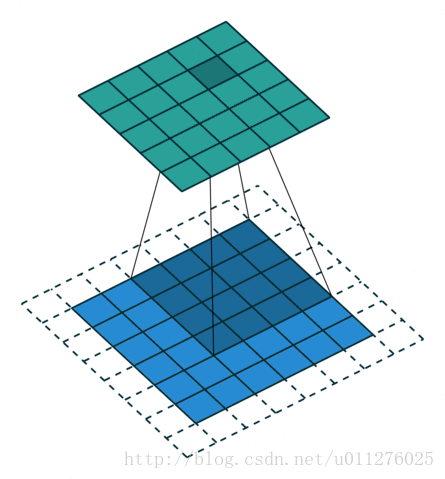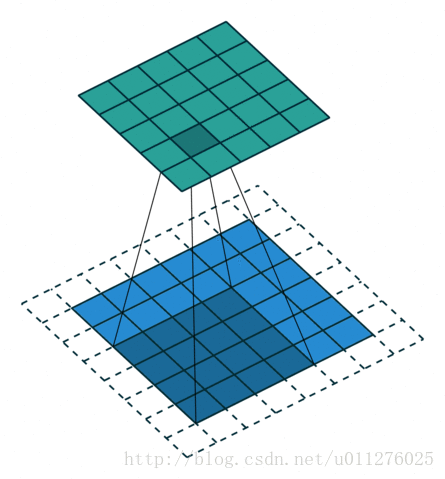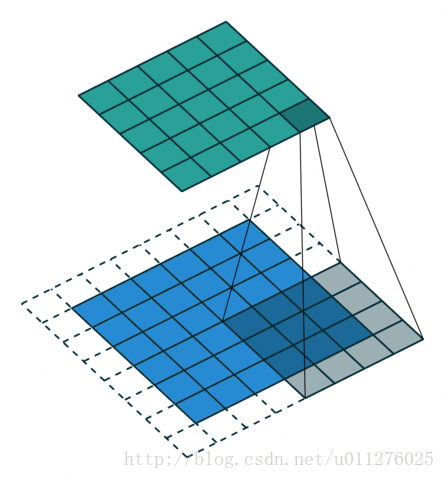
输出大小为:o′=i′+(k−1)−2p
解释:o′=(i′+2p′−k′)+1=i′+2(k−p−1)−k+1=i′+k−1−2p
注意:p′的重新计算和o′中使用的是p
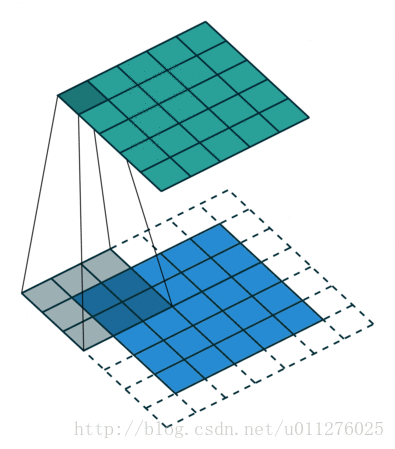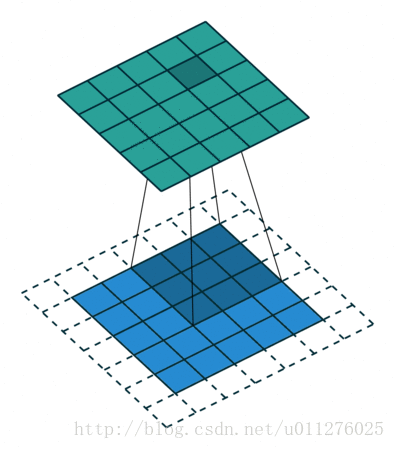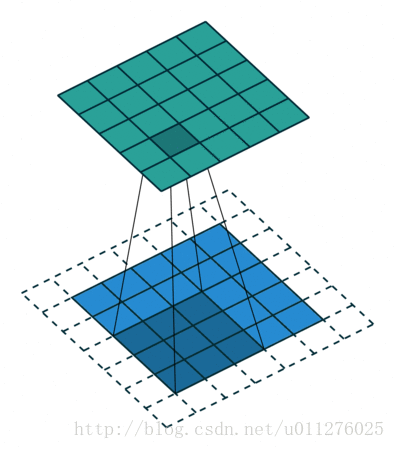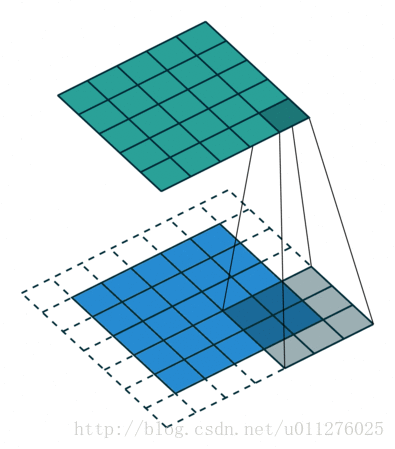
输出大小为:o=i+2⌊k/2⌋−(k−1)=i+2n−2n=i
即, k′=k,p′=p,s′=s
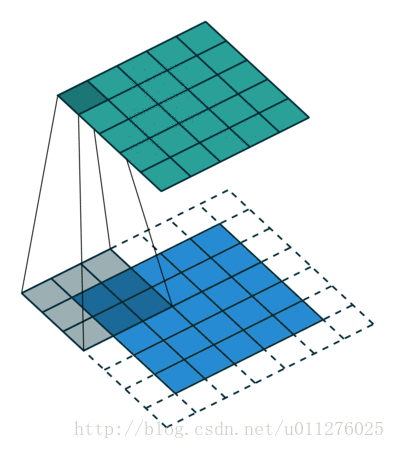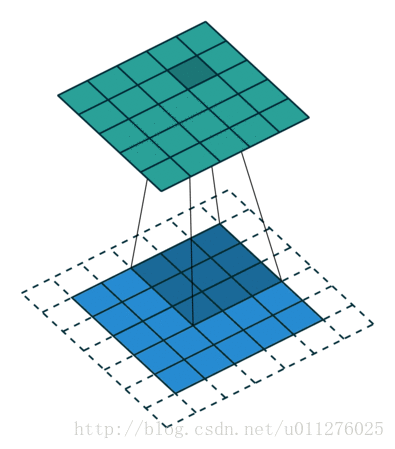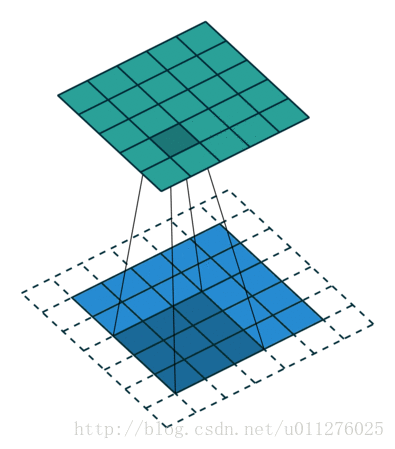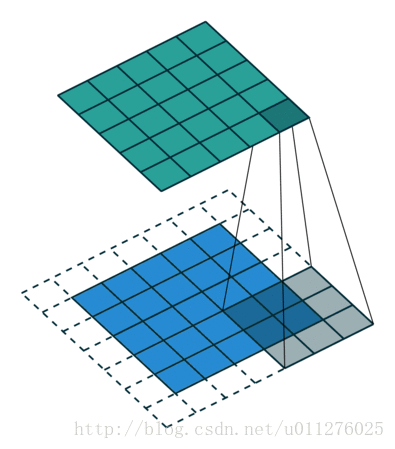
输出大小为:o′=i′+(k−1)−2p=i′+2n−2n=i′
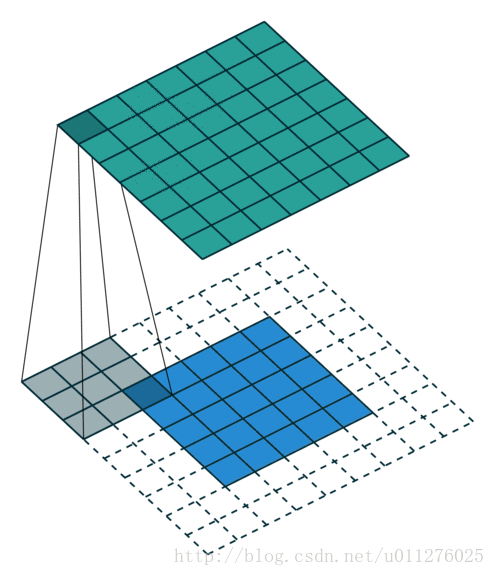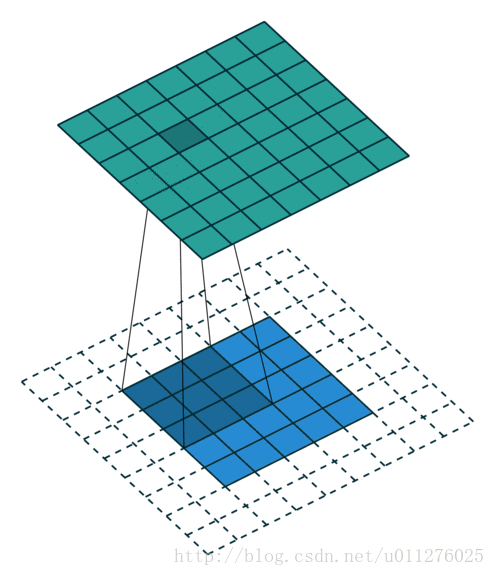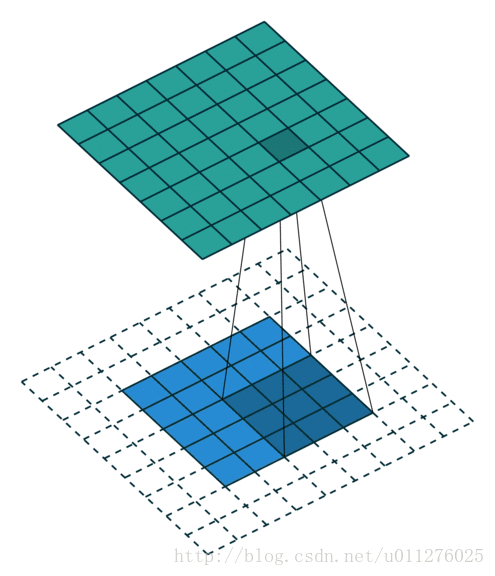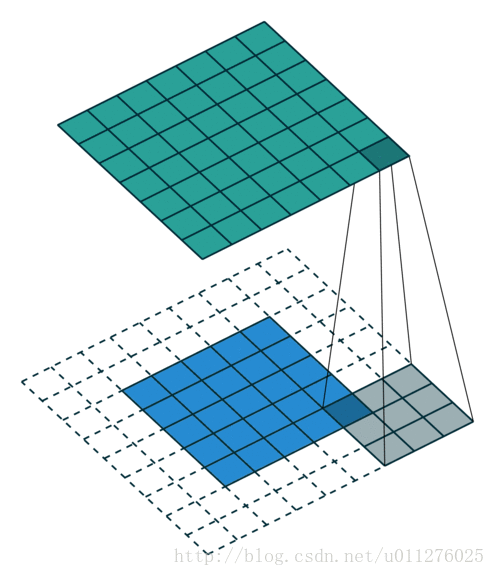
输出大小为:o=i+2(k−1)−(k−1)=i+(k−1)
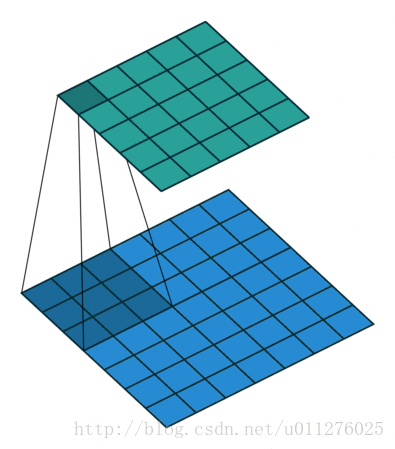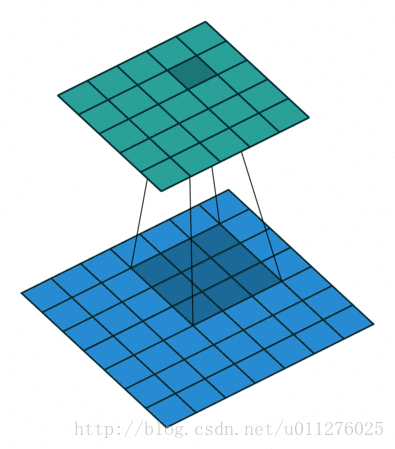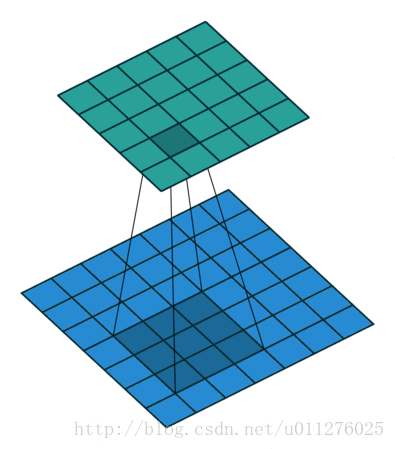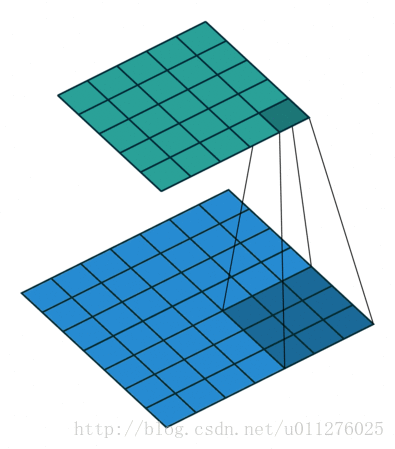
输出大小为:o′=i′+(k−1)−2p=i′−(k−1)
注意:使用的是p。
输出大小为:o=⌊i−ks⌋+1
注意:上式进行了向下取整,也就是遇到奇数无法除尽的时候需要向下取整。这种情况需要额外注意,因为在反卷积中需要在其上面和左边补0, 该图在下一节一起放出。

核:k′=k,stride:s′=1,padding:p′=k−1
注意i′的大小为在输入中插入了s - 1个0。
输出大小为:o′=s(i′−1)+k

输出大小为:o=⌊i+2p−ks + 1
核:k′=k,stride:s′=1,padding:p′=k−p−1
输出大小为:o′=s(i′−1)+k−2p
对于无法整除的
这种情况需要在输入矩阵的上边和右边增加a排0,其中a=(i+2p−k)
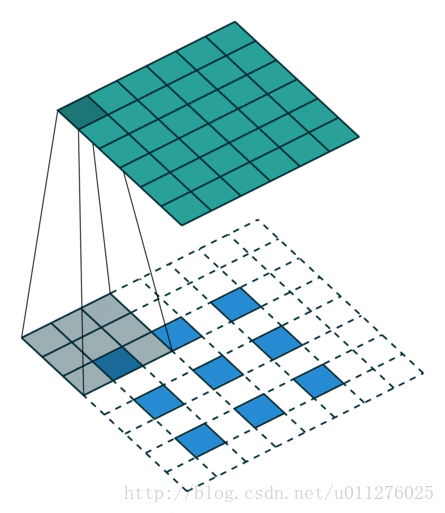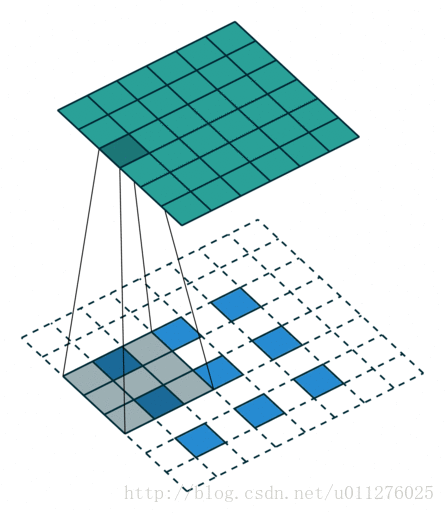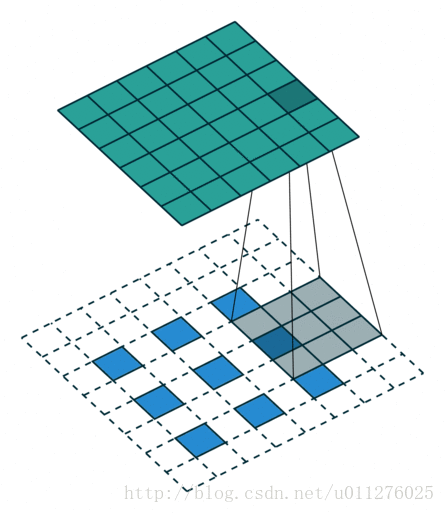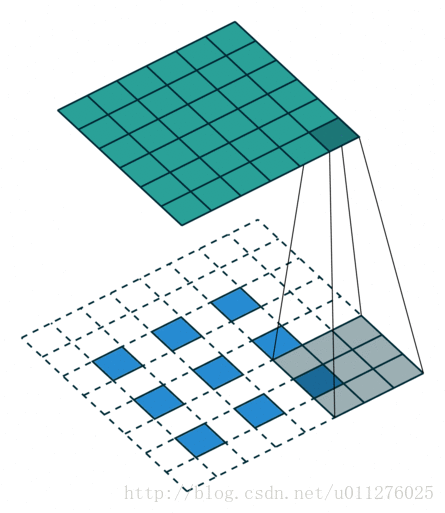
输出大小为:o′=s(i′−1)+k+a−2p
文章参考:A guide to convolution arithmetic for deep learning
首先是卷积和反卷积的输入和输出形状(shape)大小,受到padding、strides和核的大小的影响。其计算如下:
| 操作 | 卷积 | 反卷积 |
|---|---|---|
| non padding,no strides | o = (i - k) + 1 | o’ = i’ + (k - 1) |
| arbitrary padding, no strdies | o = (i - k) + 2p + 1 | o’ = i’ + (k - 1) - 2p |
| half padding, no strides | o = i | o’ = i’ |
| full padding, no strides | o = i + (k - 1) | o’ = i’ - (k - 1) |
| non padding, non-unit strides | o = ⌊i−ks⌋+1 | o’ = s(i’ - 1) + k |
| arbitrary padidng, non-unit strides | o = ⌊i+2p−ks⌋+1 | o′=s(i′−1)+k−2p能被strides整除o′=s(i′−1)+a+k−2p不能被strides整除 |
卷积操作
关于在数学上的卷积公式就不多说了,全是一堆公式,在图像中卷积的应用而且有点不一样,直接上一个ufldl的神图,初始接触卷积就是看的这个教程。
就是通过一个卷积核在图片像素中移动进行计算,同时,这种平移计算卷积的操作也可以看成矩阵操作,对于上面一个输入为5x5的输入,核为3x3的卷积来说(无padding且1 strides),把输入、卷积核和输出都展开为向量形式:
输入为25维的列向量 x
x=[11100...01100]
核扩充为9x25维的矩阵 C
C=⎡⎣⎢⎢⎢⎢w0,00...0w0,1w0,00w0,2w0,10w0,3w0,200w0,30000.........⎤⎦⎥⎥⎥⎥=⎡⎣⎢1...00010000000......⎤⎦⎥
输出为4维的行向量y=Cx
x=[434243234]
前向传播
通过上述的矩阵表示,则前向传播可以表示为:y=Cx
反向传播
神经网络的反向传播是通过链式求导计算的,后一层的误差乘以导数得到前一层的误差。则每层的梯度为:∂L∂y⋅∂y∂x则对于单个xj有:
∂L∂xj=∑i∂L∂yi⋅∂yi∂xj=∑i∂L∂yi⋅Ci,j=∂L∂y⋅C∗,j=CT∗,j⋅∂L∂y
则对于x有:
∂L∂x=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢∂L∂x1∂L∂x2...∂L∂xn⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥= ⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢CT∗,1⋅∂L∂yCT∗,2⋅∂L∂y...CT∗,n⋅∂L∂y⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥=CT⋅∂L∂y
反卷积操作(transposed convolution)
反卷积,其实就是卷积转置(transposed convolution),也称为微步卷积(fractionally strided convolutions),因为在反卷积中可能出现移动小于一步的情况,下面会介绍。根据上面矩阵表示卷积的前向和反向传播的过程,其反卷积的操作就非常简单了,只需要对C进行转置就好了,C′=CT.
即:
x=CTy
∂L∂x=C⋅∂L∂y
因此,在反卷积中不需要改变核的大小。
不使用padding和strides
卷积操作
这种类型是最简单的
输出大小为:o=(i−k)+1
解释: 只看一次重做到右的滑动,一共滑动i−k次,在加上本身初始所在的位置,所以输出为(i−k)+1。
反卷积操作
为了使得到的输出结果比输出结果的shape大,需要改变其padidng的值。k’ = k
s’ = s
p’ = k-1
解释:k和s在反卷积中不改变,卷积操作使得输出减小了k−1, 则反卷积操作需要使输出还原到原大小,即输出增加k−1, 得:i′+(k−1)=(i′+2p′−k′)+1 –> p′=k−1.
其过程如下所示:

输出大小为:o′=i′+(k−1)
解释:o′=(i′+2p′−k′)+1=i′+(k−1)
使用padding和不使用strides
卷积操作
使用padding在输入图像周围填充0,使输出的结果shape大于输入的结果(不是反卷积)。在实际实现卷积操作中没有计算这些0的乘法
输出大小为:o=(i−k)+2p+1
**解释:**padding在矩阵周围增加了p个单位的0,因此其输入大小增加为i+2p, 即,o=(i+2p−k)+1
反卷积操作
由于在卷积时在输入的四周补0了,所以在反卷积时需要重新计算p′, p′=k−p−1.解释:同理,卷积操作减少了k−2p−1, 在反卷积中需要增加回来,则,i′+(k−2p−1)=(i′+2p;−k′)+1 –> p=k−p−1.

输出大小为:o′=i′+(k−1)−2p
解释:o′=(i′+2p′−k′)+1=i′+2(k−p−1)−k+1=i′+k−1−2p
注意:p′的重新计算和o′中使用的是p
奇数核一半的padding和不使用strides
这种结构比较好玩,就是使输入和输出的大小相同,VGG就是使用这种结构。卷积操作
核:k=2n+1,,stride:s=1,padding:p=⌊k/2⌋=n
输出大小为:o=i+2⌊k/2⌋−(k−1)=i+2n−2n=i
反卷积操作
由于卷积的输入和输出的形状相同,则反卷积操作与卷积操作也相同。即, k′=k,p′=p,s′=s

输出大小为:o′=i′+(k−1)−2p=i′+2n−2n=i′
奇数核-1大小的padding和不使用strides
stride:s=1,padding:p=k−1。卷积操作
输出的结果比输入的大,输出增加了p大小。
输出大小为:o=i+2(k−1)−(k−1)=i+(k−1)
反卷积操作
相当于没有使用padding的反卷积操作,就是卷积操作中输出增加了k−1,则在反卷积中不使用padding,则输出大小减少k−1。
输出大小为:o′=i′+(k−1)−2p=i′−(k−1)
注意:使用的是p。
不使用padding和使用strides
即,卷积核一次移动多步。卷积操作

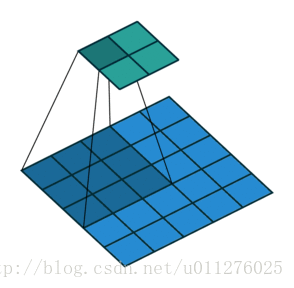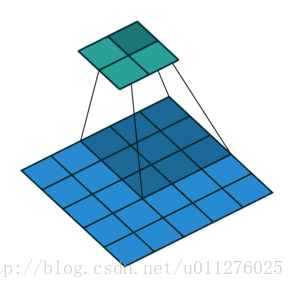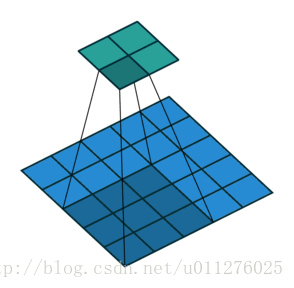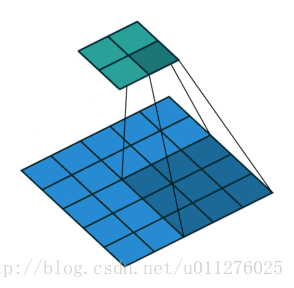
输出大小为:o=⌊i−ks⌋+1
注意:上式进行了向下取整,也就是遇到奇数无法除尽的时候需要向下取整。这种情况需要额外注意,因为在反卷积中需要在其上面和左边补0, 该图在下一节一起放出。

反卷积操作
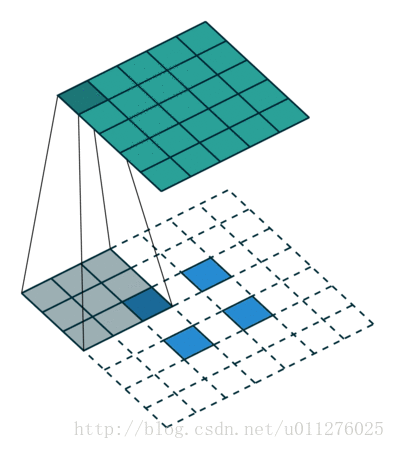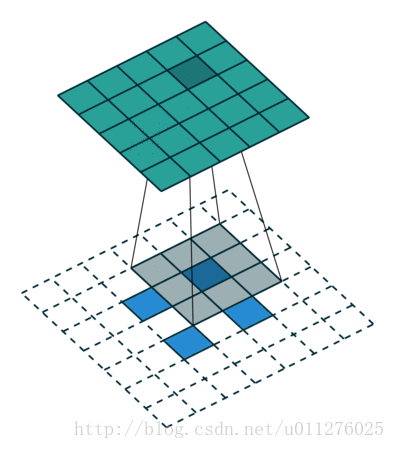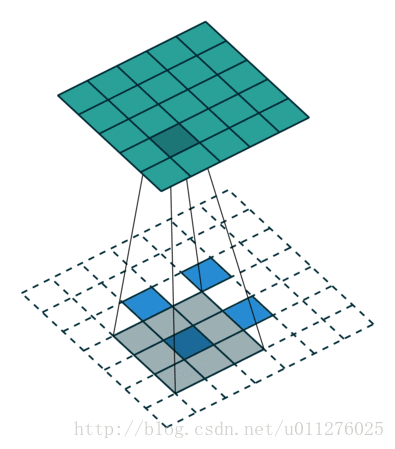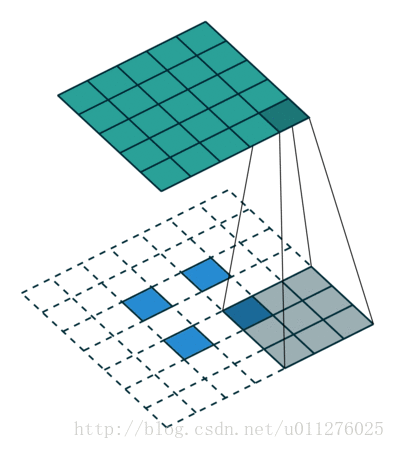
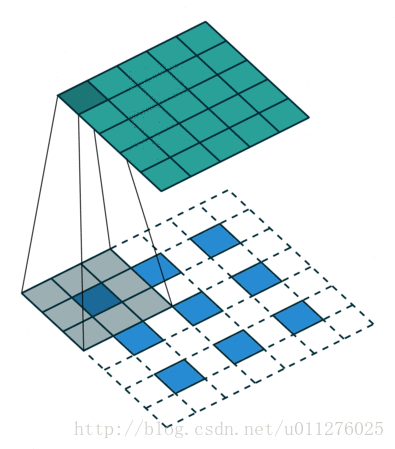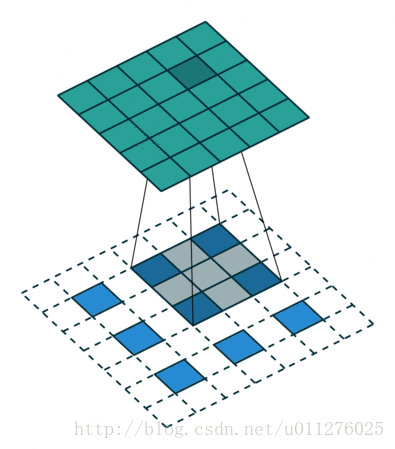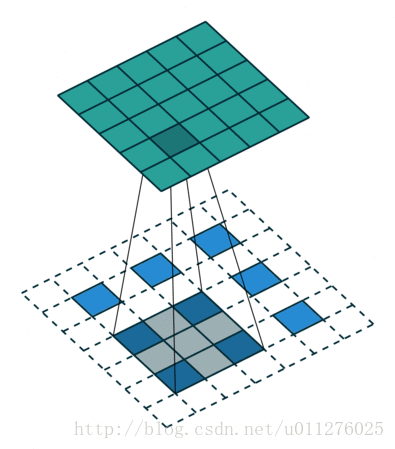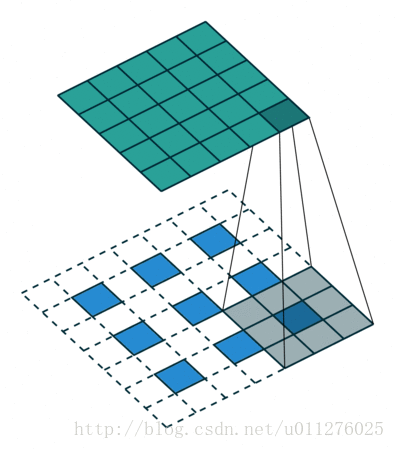
这种情况的反卷积比较好玩,需要在输入数据中插0。这也是微步卷积的由来(fractionally strided convolutions),由于在输入中插入0,导致strides移动<1。核:k′=k,stride:s′=1,padding:p′=k−1
注意i′的大小为在输入中插入了s - 1个0。

输出大小为:o′=s(i′−1)+k
使用padding和使用strides
卷积操作
和不使用padding差不多,只不过四周补0了.
输出大小为:o=⌊i+2p−ks + 1
反卷积操作
对于移动步数刚好整除的核:k′=k,stride:s′=1,padding:p′=k−p−1

输出大小为:o′=s(i′−1)+k−2p
对于无法整除的
这种情况需要在输入矩阵的上边和右边增加a排0,其中a=(i+2p−k)

输出大小为:o′=s(i′−1)+k+a−2p
references
图片来自:https://github.com/vdumoulin/conv_arithmetic文章参考:A guide to convolution arithmetic for deep learning
相关文章推荐
- 卷积神经网络理解与实现
- caffe中LetNet-5卷积神经网络模型文件lenet.prototxt理解
- 个人对sparse在神经网络学习中的一些理解
- 【论文学习】神经光流网络——用卷积网络实现光流预测(FlowNet: Learning Optical Flow with Convolutional Networks)
- 深度学习(四)卷积神经网络入门学习
- 深度神经网络结构以及Pre-Training的理解
- SVM神经网络的术语理解
- 理解卷及神经网络应用在自然语言处理的学习笔记
- 神经网络入门(二)卷积网络在图像识别的应用
- 神经网络(10)--有助于对神经网络Backpropagation算法的理解
- 深度学习之卷积神经网络入门(2)
- 深度学习之卷积神经网络总结
- 神经网络的通俗理解
- 深度神经网络结构以及Pre-Training的理解
- 深度学习与自然语言处理之四:卷积神经网络模型(CNN)
- 径向基(Radial basis function)神经网络、核函数的一些理解
- 深度神经网络结构以及Pre-Training的理解
- [我们是这样理解语言的-3]神经网络语言模型(续)
- 深度学习与自然语言处理之四:卷积神经网络模型(CNN)
- 全卷积网络:从图像级理解到像素级理解
