期望最大化算法(The EM algorithm)
2017-04-12 10:27
218 查看
在上一章中,我们为了解决拟合混合高斯模型的拟合问题已经接触了EM算法。这一章里,我们会进一步扩展EM算法的应用,你会发现它可以用于解决一大类包含隐参数的估计问题。让我们从Jensen不等式开始我们的讨论。
定理. 设f是一个凸函数,X是一个随机变量。那么:
E[f(X)]≥f(EX).
不仅如此,若f为严格凸时,那么E[f(X)]=f(EX)当且仅当X=E[X]的概率为1时发生。关于定理的阐述我们可以看看下面这张图片:
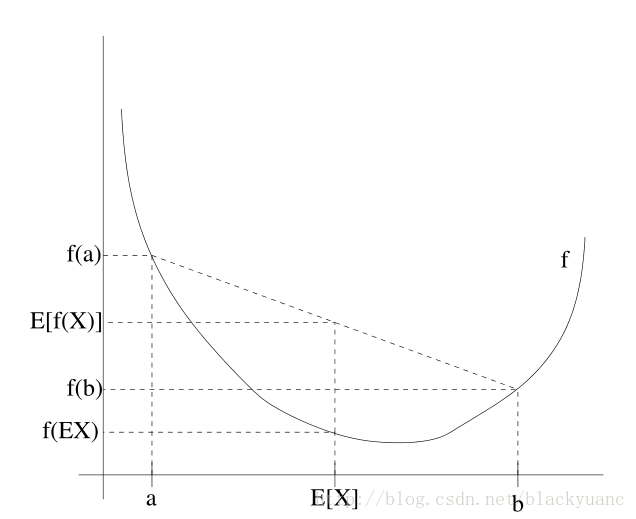
图中凸函数f是实线绘制的曲线,随机变量X有50%的概率是a,50%的概率是b,所以X的期望是a,b的中点。从这个例子可以看到,只要f是凸函数,必有E[f(X)]≥f(EX)。
ℓ(θ)=∑i=1mlog p(x;θ)=∑i=1mlog∑zp(x,z;θ).
由于无法直接求解参数θ的极大似然估计,引入隐参数z(i),如果假设隐参数的值已知,那么求解极大似然估计就会变得很容易。
这时求最大似然估计,EM算法是一个行之有效的方法。直接最大化ℓ(θ)很困难,但我们的策略是先构造ℓ的下界(E步骤),再最优化其下界(M步骤)。过程如下图所示

对每一个i,设z服从Qi分布(∑zQi(z)=1,Qi(z)≥0),则下式成立:
∑ilogp(x(i);θ)=∑ilog∑z(i)p(x(i),z(i);θ)=∑ilog∑z(i)Qi(z(i))p(x(i),z(i);θ)Qi(z(i))=∑ilog Ez(i)∼Qi[p(x(i),z(i);θ)Qi(z(i))]≥∑iEz(i)∼Qi [logp(x(i),z(i);θ)Qi(z(i))]≥∑i∑z(i)Qi(z(i)) logp(x(i),z(i);θ)Qi(z(i))(1)(2)(3)
因为f′′(x)=−1/x2<0,f(x)=log x是一个凹函数。第四步可以根据Jensen不等式求得。
对于任意的分布Qi,方程(3)给出了对数似然函数ℓ(θ)的下界。这时Qi分布有很多可能的选择,我们应该如何决定呢?如果我们现在有关于参数θ的假设值,那么很自然下界的选择要和θ相关。
要使下界的选择与θ相关,我们需要推导中使用Jensen不等式的地方变为相等。为此期望值需要是一个常数变量。则有:
p(x(i),z(i);θ)Qi(z(i))=c
为使常数c不依赖z(i)的取值。我们需要Qi(z(i))与p(x(i),z(i);θ)成比例。
实际上因为∑zQi(z(i))=1,这进一步告诉我们:
Qi(z(i))=p(x(i),z(i);θ)∑zp(x(i),z(i);θ)=p(x(i),z(i);θ)p(x(i);θ)=p(z(i)|x(i);θ)
我们令Qi为给定x(i)与参数θ关于z(i)的后验概率。
通过选择Qi,我们求对数似然函数的最大下界,这是E阶段。通过改变参数θ,我们求方程(3)中的最大值。重复执行一上两个步骤就是EM算法:
循环至收敛 {
(E步骤)对每个i,令:
Qi(z(i))=p(z(i)|x(i);θ).
(M步骤) 令:
θ:=arg maxθ∑i∑z(i)Qi(z(i)) logp(x(i),z(i);θ)Qi(z(i))
}
EM算法是一个一致收敛的算法。我们在算法描述时说循环至收敛。实际情况下判断收敛的方式一般为,当对数函数的增长小于某一设定值时,我们认为EM算法继续改善的能力已经很小了,即认为其收敛。
1 Jensen 不等式
设f是一个定义域为实数的函数,回忆前面的内容,当f′′(x)≥0是函数f就是一个凸函数(下凸)。而当f的输入是一个向量时,当它的海森矩阵是一个半正定矩阵时,我们可以说函数f是一个严格凸函数。Jensen不等式的表述如下:定理. 设f是一个凸函数,X是一个随机变量。那么:
E[f(X)]≥f(EX).
不仅如此,若f为严格凸时,那么E[f(X)]=f(EX)当且仅当X=E[X]的概率为1时发生。关于定理的阐述我们可以看看下面这张图片:

图中凸函数f是实线绘制的曲线,随机变量X有50%的概率是a,50%的概率是b,所以X的期望是a,b的中点。从这个例子可以看到,只要f是凸函数,必有E[f(X)]≥f(EX)。
2 EM算法
设某估计问题中有m个独立的样本{x(1),…,x(m)}。我们希望使模型p(x,z)的参数和数据拟合,则对数似然函数写成如下形式:ℓ(θ)=∑i=1mlog p(x;θ)=∑i=1mlog∑zp(x,z;θ).
由于无法直接求解参数θ的极大似然估计,引入隐参数z(i),如果假设隐参数的值已知,那么求解极大似然估计就会变得很容易。
这时求最大似然估计,EM算法是一个行之有效的方法。直接最大化ℓ(θ)很困难,但我们的策略是先构造ℓ的下界(E步骤),再最优化其下界(M步骤)。过程如下图所示

对每一个i,设z服从Qi分布(∑zQi(z)=1,Qi(z)≥0),则下式成立:
∑ilogp(x(i);θ)=∑ilog∑z(i)p(x(i),z(i);θ)=∑ilog∑z(i)Qi(z(i))p(x(i),z(i);θ)Qi(z(i))=∑ilog Ez(i)∼Qi[p(x(i),z(i);θ)Qi(z(i))]≥∑iEz(i)∼Qi [logp(x(i),z(i);θ)Qi(z(i))]≥∑i∑z(i)Qi(z(i)) logp(x(i),z(i);θ)Qi(z(i))(1)(2)(3)
因为f′′(x)=−1/x2<0,f(x)=log x是一个凹函数。第四步可以根据Jensen不等式求得。
对于任意的分布Qi,方程(3)给出了对数似然函数ℓ(θ)的下界。这时Qi分布有很多可能的选择,我们应该如何决定呢?如果我们现在有关于参数θ的假设值,那么很自然下界的选择要和θ相关。
要使下界的选择与θ相关,我们需要推导中使用Jensen不等式的地方变为相等。为此期望值需要是一个常数变量。则有:
p(x(i),z(i);θ)Qi(z(i))=c
为使常数c不依赖z(i)的取值。我们需要Qi(z(i))与p(x(i),z(i);θ)成比例。
实际上因为∑zQi(z(i))=1,这进一步告诉我们:
Qi(z(i))=p(x(i),z(i);θ)∑zp(x(i),z(i);θ)=p(x(i),z(i);θ)p(x(i);θ)=p(z(i)|x(i);θ)
我们令Qi为给定x(i)与参数θ关于z(i)的后验概率。
通过选择Qi,我们求对数似然函数的最大下界,这是E阶段。通过改变参数θ,我们求方程(3)中的最大值。重复执行一上两个步骤就是EM算法:
循环至收敛 {
(E步骤)对每个i,令:
Qi(z(i))=p(z(i)|x(i);θ).
(M步骤) 令:
θ:=arg maxθ∑i∑z(i)Qi(z(i)) logp(x(i),z(i);θ)Qi(z(i))
}
EM算法是一个一致收敛的算法。我们在算法描述时说循环至收敛。实际情况下判断收敛的方式一般为,当对数函数的增长小于某一设定值时,我们认为EM算法继续改善的能力已经很小了,即认为其收敛。
相关文章推荐
- 【the EM algorithm】期望最大化
- 十大经典数据挖掘算法之EM(期望最大化)算法
- Expectation Maximization-EM(期望最大化)-算法以及源码
- EM-期望最大化算法
- 机器学习算法(优化)之二:期望最大化(EM)算法
- Expectation Maximization-EM(期望最大化)-算法以及源码
- 图像处理基础知识系列之四:最大似然和EM(期望最大化)算法简单梳理
- 期望最大化(EM)算法(讲的很好)
- EM 期望最大化算法
- 机器学习算法(优化)之二:期望最大化(EM)算法
- EM(期望最大化)算法(1):初探原理
- 期望最大化算法(Expectation Maximum, EM)
- 期望最大化(EM)算法
- EM(期望最大化)算法初步认识
- 期望最大化(EM)算法与高斯混合模型(GMM)证明
- 期望最大化算法EM
- 期望最大化(EM)算法(讲的很好)
- 高斯混合模型(GMM)及其求解(期望最大化(EM)算法)
- (EM算法)The EM Algorithm
- maximum likelihood estimation( 极大似然估计 ) - 无完整数据的参数估计 --- Expectation Maximization ( 期望最大化 ) 算法
