视觉定位原理：对极几何与基本矩阵

对极几何与基本矩阵

标签（空格分隔）： slam

对极几何

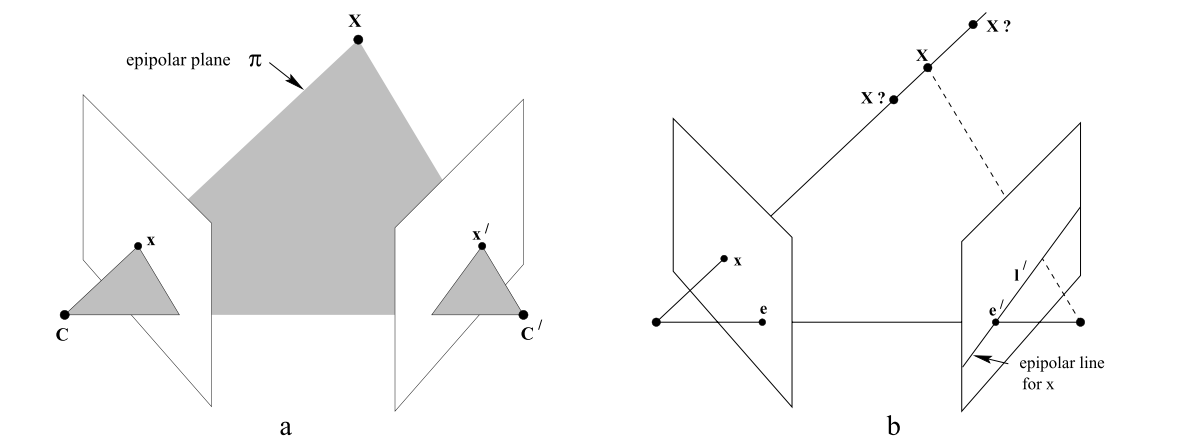
本质上两幅图之间的对极几何是图像平面与以基线为轴的平面束的交的几何，这种几何被广泛同于双目成像原理中

如图所示，摄像机由相机中心C,C’以及各自的成像平面表示，对于任意一个空间中的点X,在两个像平面上的点分别为x,x’，第一幅图像上的点x反向投影成空间三维的一条射线，它由摄像机中心和x确定，这条射线向第二个图像平面上投影得到一条直线l’，显然x的投影x’必然在l’上



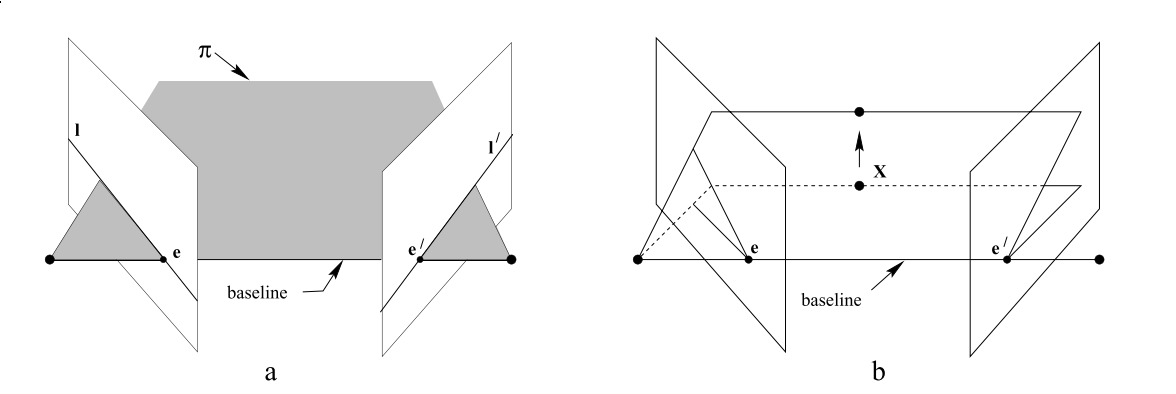
如图所示，我们把相机中心的连线叫做基线(baseline),基线与两幅图像平面交于对极点e和e’，任何一条包含基线的平面pi是一张对极平面，分别与图像平面相交于l和l’，实际上，当三维位置X变化时，对应的实际上是该对极平面绕基线”旋转”，这个旋转得到的平面簇叫做对极平面束，由所有对极平面和成像平面相交得到的对极限相交于对极点

汇交相机

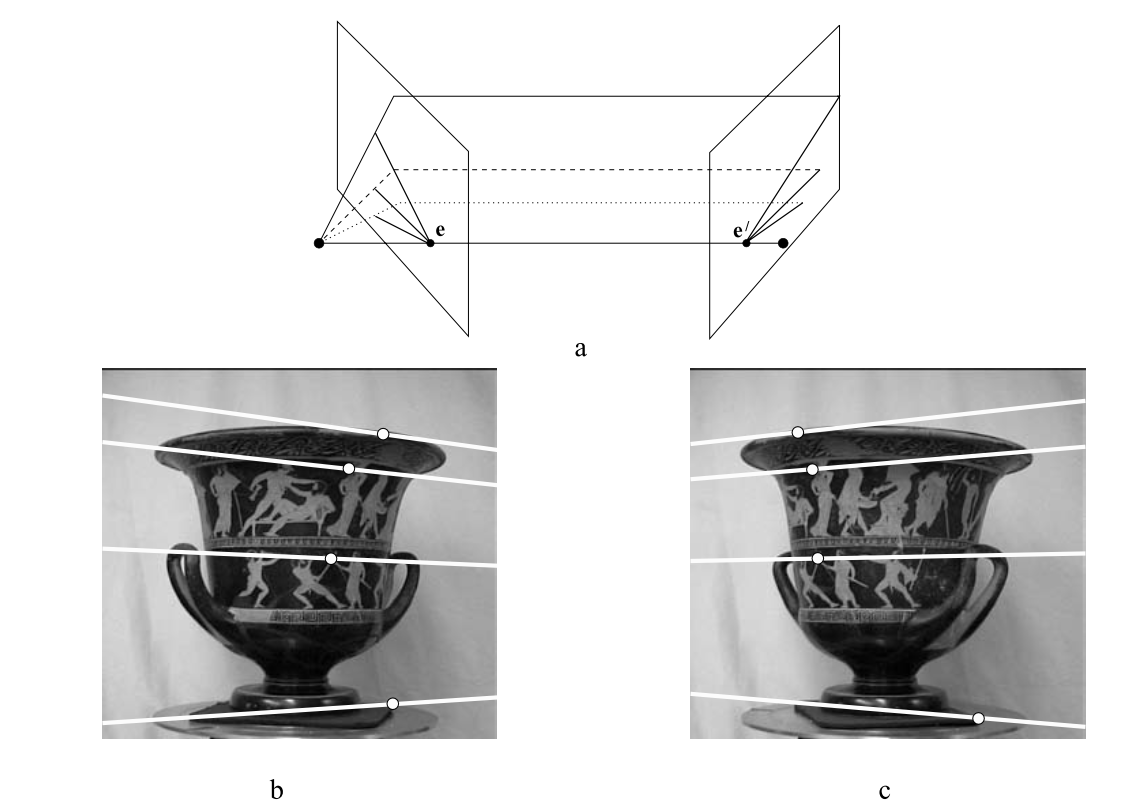
汇聚摄像机的对极几何是比较一般的情形，如b,c图所示，视图之间的运动是一个平移加上旋转

平行于图像平面的运动

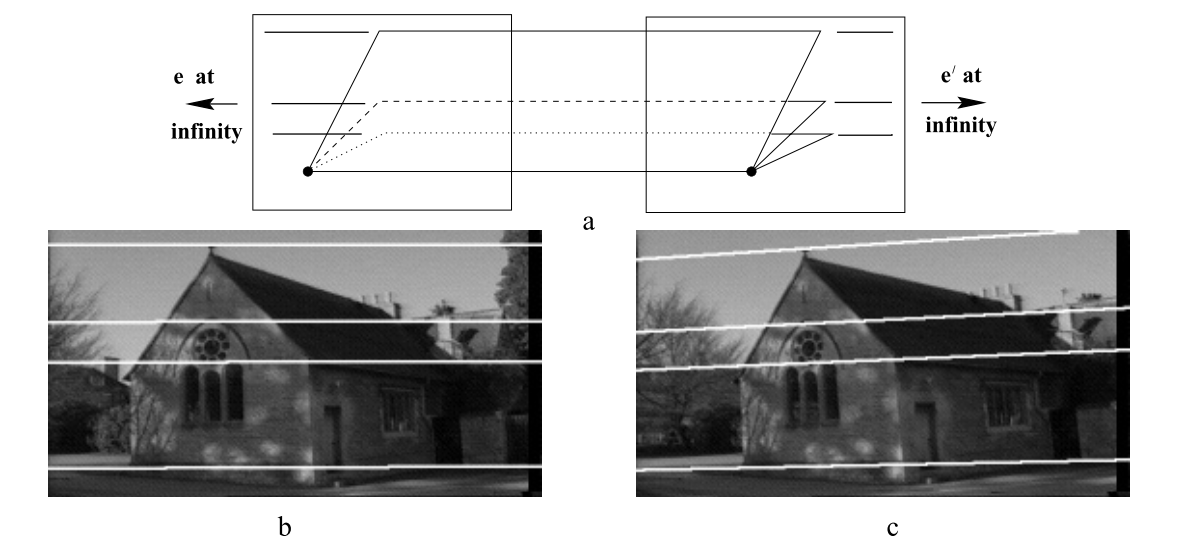
平行于图像的平移运动是运动的特殊情况，基线与图像平面相交于无穷远，因此对极点是无限远点，对极线是平行线

基本矩阵F

基本矩阵是对极几何的代数表示，我们已经知道对于一幅视图上的点x，在另一视图上有一条对应的极线l’,该点的对应点x’必然在l’上，因此存在映射: x-> l’,基本矩阵F实际上就是表示这样的一种点到直线的射影映射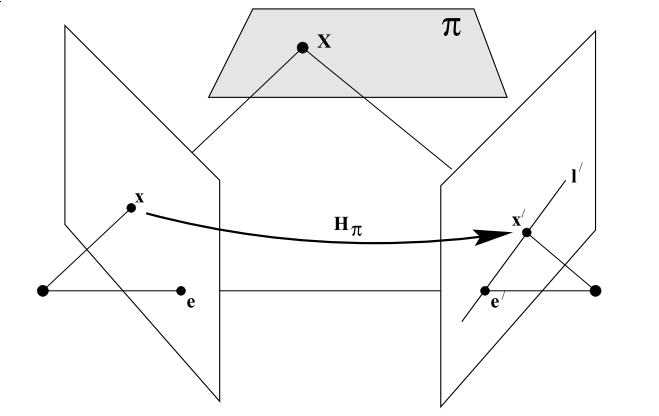



如图所示，考虑空间中不通过任何两个摄像机中心的平面pi,过第一个相机中心C和x的射线与该平面pi交于X,这个点再投影到第二幅图像上的点x’，这个过程通过平面pi的平移。由于X在对应与x的射线上，所以投影点x’必然在对应于这条射线的图像即极限l’上，点x和x’都是在一张平面上的3D点X的像，在第一幅图像上的所有点xi和对应点x’i的射影实际上是等价的，因为他们都射影等价于共面点集Xi，所以存在一个2D映射H,把每一个xi映射到x’i

给定点x’,通过x’和对极点e’的对极线I’，可以记为I’=e’ * x’ = [e’]x’，又因为x’=Hx，所以必然有

I’ = [e’]Hx = Fx

以下部分是多视角几何的原文：



我在这里解释一下，由于射影变换是一个不满秩的映射，由此，对于一个射影映射的逆映射，会映射成一条直线X(lambda)



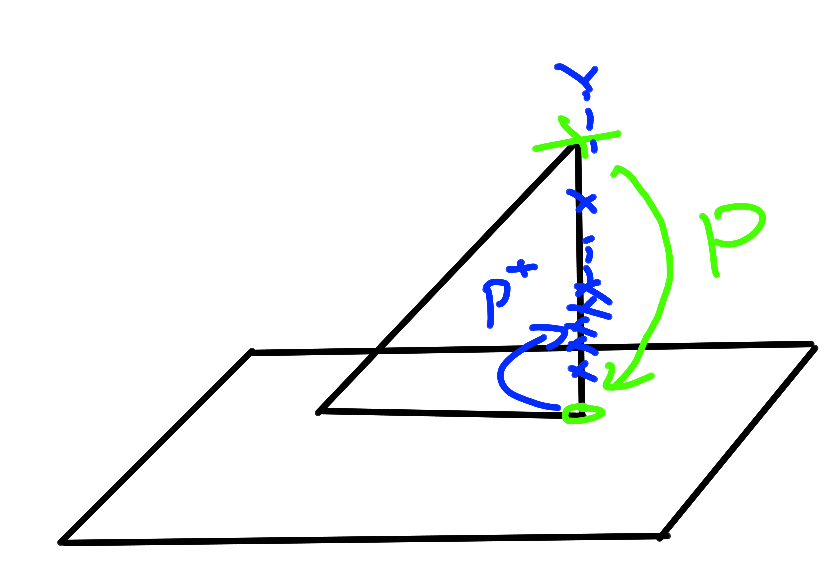
由于这条射线是由点x和相机中心表示的，自然X(lambda)如文献中公式所示

由于这个射线向另一张图片上的投影问P’所以自然而然将另一幅图的对极点和X在另一幅图的投影表示为



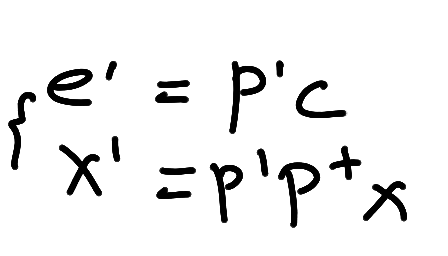
由于l’ = e’叉乘x’所以最后得到公式9.1，即



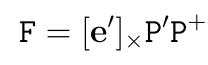
最后，由于l’ = Fx,x’又在直线l’上，所以x’l’ = x’Fx = 0

本质矩阵

通过以上部分，你会发现，基本矩阵F，只和图像有关和空间位置实际上没啥关系，实际上你会发现，只要算出一个F，他可以由多种投影矩阵得到，由公式4.9，假如两个相机都超同一方向旋转R，那么F还是不会有任何变化，因此我们需要对相机投影矩阵进行一种规定

由此，引入归一化坐标，考虑分解P = K[P|t]的摄像机矩阵，领x=PX为图像上点，假如给定标定矩阵K，用它的逆作用于x，得到新的x”，那么必然有x”=[R|t]X，其中x”叫做图像上点的归一化坐标下的表示由此[R|t]记为归一化相机矩阵

考虑一对归一化相机矩阵P=[I|0]以及P’=[R|t]，在这对归一化矩阵下得到的基本矩阵称为本质矩阵



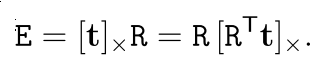
实际上由于[t]是三维的叉积矩阵，所以自然是一个反对称矩阵，所以很容易可以得到E = SR,其中S是反对称矩阵

根据极分解定理，S=kUZU^T，Z = [0,1,0;-1,0,0;0,0,0]

但由SVD分解可以得到E = Udiag(1,1,0)V^T

由于Udiag(1,1,0)V^T=(UZU^T)(UXV^T)=U(ZX)V^T，其中X为某种旋转

实际上得到ZX=diag(1,1,0),其中X是旋转矩阵,若假设W=[0,-1,0;1,0,0;0,0,1]那么可以得到X=W或者X=W^T

最终可以得到书上的结论9.18和9.19









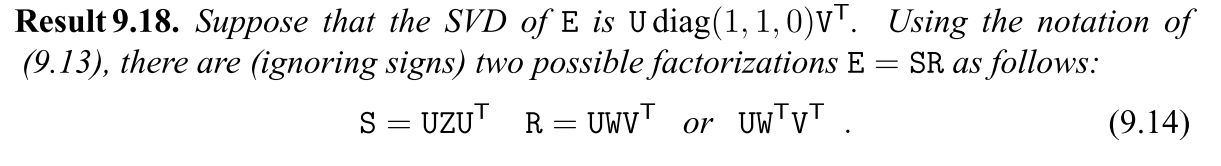
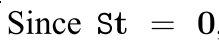
S = [t]表达的意思是叉积，自己叉自己等于0