利用java求积分(定积分和无穷限积分)
2016-05-18 11:44
696 查看
【0】README
0.1)本文部分文字描述转自或译自 https://en.wikipedia.org/wiki/Simpson%27s_rule和 href="https://en.wikipedia.org/wiki/Numerical_integration#Methods_for_one-dimensional_integrals" target=_blank>https://en.wikipedia.org/wiki/Numerical_integration#Methods_for_one-dimensional_integrals;旨在利用java求积分;(定积分和无穷限积分)
0.2)you can also refer to this link for source code: https://github.com/pacosonTang/postgraduate-research/tree/master/integration
0.3)o m g. CSDN编辑器掉链子,无法正常显示source code, 大家凑合着看吧。oh.
【1】求定积分
1)intro:由 wikepedia 上关于 辛普森法的intro 以及 《高等数学第6版上册同济版》p229 关于定积分的近似计算中提到的辛普森法,本文求定积分的方法采用了辛普森近似法;
2)下面引用《高等数学第6版上册同济版》p229 关于辛普森法的描述
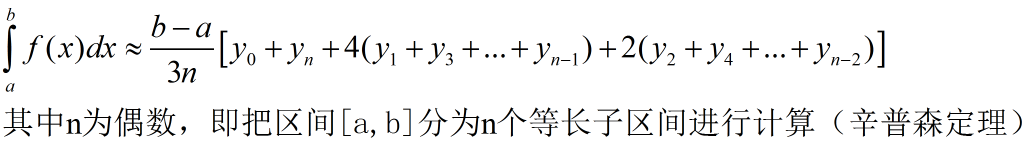
3)计算函数定积分的源代码如下:
Attention)
A1)以上测试用例中涉及到的积分函数来自 《高等数学第6版上册同济版》p230的例2;
A2)定积分表达式为
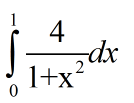
【2】求无穷限积分(本文以求标准正态分布的无穷下限反常积分为例)
1)求无穷限积分是基于定积分的;如何求定积分,本文在章节【1】中已经讲了;

2)所以标准正态分布的无穷下限反常积分函数可转化为:

3)计算标准正态分布无穷下限积分的测试用例如上所示。
Attention)
A1)上述求标准正态分布无穷下限积分的代码对realUpper 有要求,小于等于5.0;因为当realUpper>5的话,其value=1了;
A2)需要求标准正态分布的下限积分时,强烈建议使用 integration.stdGaussValue() 其精度要高些。
0.1)本文部分文字描述转自或译自 https://en.wikipedia.org/wiki/Simpson%27s_rule和
0.2)you can also refer to this link for source code: https://github.com/pacosonTang/postgraduate-research/tree/master/integration
0.3)o m g. CSDN编辑器掉链子,无法正常显示source code, 大家凑合着看吧。oh.
【1】求定积分
1)intro:由 wikepedia 上关于 辛普森法的intro 以及 《高等数学第6版上册同济版》p229 关于定积分的近似计算中提到的辛普森法,本文求定积分的方法采用了辛普森近似法;
2)下面引用《高等数学第6版上册同济版》p229 关于辛普森法的描述
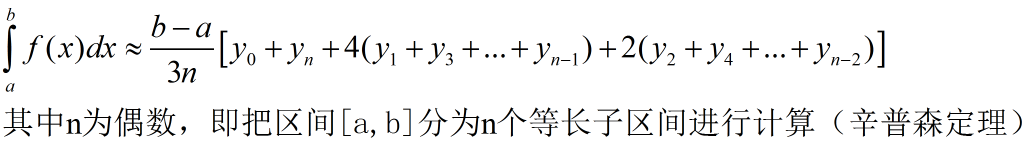
3)计算函数定积分的源代码如下:
// compute the numeric integration.
public class Integration {
public Integration(){}
// apply simpson rule to approximately compute the integration.
public double simpsonRule(double upper, double lower, int n, Function df) {
double result = 0;
double unit = (upper-lower)/n;
double factor1 = unit / 3;
double[] x = new double[n+1];
for (int i = 0; i < x.length; i++) {
x[i] = lower + unit*i;
}
for (int i = 0; i < x.length; i++) {
if(i==0 || i==x.length-1) {
result += df.fun(x[i]);
}else if(i%2 == 0) { // if i is even num.
result += 2*df.fun(x[i]);
}else { // if i is odd num.
result += 4*df.fun(x[i]);
}
}
result *= factor1;
return result;
}
// compute the standard normal distribution integration
// refer to the integration table in p382 of "probability and statistics" from ZheJiang University.
public double stdGaussValue(double realUpper) {
Integration integration = new Integration();
double upper = 1.0;
double lower = 0.0;
int n = 200; // splited into 200 subintervals.
// double realUpper = 0.03;
if(realUpper >= 5.0) {
return 1.0;
}
double result =
integration.simpsonRule(upper, lower, n, new Function() {
@Override
public double fun(double x) {
if(x==0) {
return 0;
}
double t = realUpper-(1-x)/x;
return Math.pow(Math.E, -0.5*t*t) / (x*x);
}
});
result /= Math.pow(2*Math.PI, 0.5);
result = new BigDecimal(result).
setScale(6, RoundingMode.HALF_UP).doubleValue(); // save 6 decimal places.
return result;
}
}public class IntegrationTest { //test case.
public static void main(String[] args) {
Integration integration = new Integration();
double result = integration.stdGaussValue(4.42);
System.out.println(result);
}
public static void main3(String[] args) {
Integration integration = new Integration();
double upper = 1.0;
double lower = 0.0;
int n = 50;
double realUpper = 0.39;
double result =
integration.simpsonRule(upper, lower, n, new Function() {
@Override
public double fun(double x) {
if(x==0) {
return 0;
}
double t = realUpper-(1-x)/x;
return Math.pow(Math.E, -0.5*t*t) / (x*x);
}
});
result /= Math.pow(2*Math.PI, 0.5);
result = new BigDecimal(result).
setScale(4, RoundingMode.HALF_UP).doubleValue();
System.out.println(result);
}
public static void main2(String[] args) {
Integration integration = new Integration();
double upper = 1.0;
double lower = 0.0;
int n = 10;
double result =
integration.simpsonRule(upper, lower, n, new Function() {
@Override
public double fun(double x) {
return Math.pow(Math.E, -x*x/2);
}
});
result /= Math.pow(2*Math.PI, 0.5);
System.out.println(result);
BigDecimal decimal = new BigDecimal(result).setScale(4, RoundingMode.HALF_UP);
result = Double.valueOf(decimal.toString());
System.out.println(result);
}
public static void main1(String[] args) {
Integration integration = new Integration();
double upper = 1.0;
double lower = 0;
int n = 10;
double result =
integration.simpsonRule(upper, lower, n, new Function() {
@Override
public double fun(double x) {
return 4 / (1+Math.pow(x,2.0));
}
});
System.out.println(result);
}
}Attention)
A1)以上测试用例中涉及到的积分函数来自 《高等数学第6版上册同济版》p230的例2;
A2)定积分表达式为
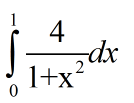
【2】求无穷限积分(本文以求标准正态分布的无穷下限反常积分为例)
1)求无穷限积分是基于定积分的;如何求定积分,本文在章节【1】中已经讲了;

2)所以标准正态分布的无穷下限反常积分函数可转化为:

3)计算标准正态分布无穷下限积分的测试用例如上所示。
Attention)
A1)上述求标准正态分布无穷下限积分的代码对realUpper 有要求,小于等于5.0;因为当realUpper>5的话,其value=1了;
A2)需要求标准正态分布的下限积分时,强烈建议使用 integration.stdGaussValue() 其精度要高些。
相关文章推荐
- java学习个人笔记---finally模块的陷阱
- 如何捕获java线程中的逃逸的异常
- java ArrayList与LinkedList 使用for,forearch,Iterator的遍历效率
- eclipse adt 搭建gradle的一些问题
- Java 字符流读取数据
- java基础重点: 面向对象,
- JAVA设计模式之抽象工厂模式
- Lambda真的挺好玩的
- LuceneTestCase Junit测试出现严重: Panic: RunListener hook shouldn't throw exceptions. java.lang.NullPointe
- 【异常处理】java.lang.NoClassDefFoundError
- Java中的继承与组合
- jdbc pool java连接池技术
- spring+mybatis+ehcache配置缓存
- spring mvc 拦截器路径问题,只拦截固定后缀
- Java实现-二叉树定义树结点及创建
- Java 对象实例化过程
- java实现身份证有效性验证
- Rxjava操作符学习博客
- 工厂模式
- 快速排序算法Java
