三角网格数据结构-2
2016-05-17 01:05
375 查看
基本Mesh结构
上篇文章讲述了一般的基本的Mesh应该至少包含点集和三角形集合的信息,也就是类似如下的定义方式:
本篇继续介绍Mesh相关的一些算法,包括计算面法向,邻接面,点法向,邻接点,以及拉普拉斯平滑算法,同时丰富了Mesh的成员。
计算面法向量
面法向量是Mesh中每一个三角形的法向量的集合,要得出这个集合,就应当为这个Mesh的每一个三角形计算法向量。注意,在立体几何中,一个面的法向量是方向垂直于这个面的向量(注意这里的向量都是指单位向量)。也就是说,对于一个面,这个面的法向量其实有两个方向,比如下图的平面。它的法向量既可以指向上面也可以指向下面。

但是对于Mesh中的三角形,法向量的方向是有讲究的,对于一个按P0、P1、P2顺序存储的三角形,它的法向量方向是符合右手法则的方向。就是用右手按P0、P1、P2的方向握过去,大拇指所指的方向,即下图的向上的向量,向下的向量是错误的。

区分法向量的方向是为了计算机图形的渲染,在渲染的时候,一般视法向量正对的方向为三角形的正面,而另一个相反的方向则是背面,在单侧光进行照射的时候,正面会根据材质进行适当的反光而显得明亮,而背面则暗淡一些。详细的关于光线照射这方面的信息,可以参考相应的书籍,本文就不再多述。
根据几何上对向量叉积的定义,面法向量可以使用三角形边向量的叉积计算:

为此特别定义向量Vector结构,同时在Mesh类中添加存储面法向的成员数组FaceNormals,类型为std::vector<Vector>,相应的代码如下:
计算邻接面
求邻接面,或者说邻接三角形,简单的说就是对Mesh中的任何一个点,求出包含这个点的三角形的集合。如下图所示,对于点V而言,它的邻接面就是被标记为红色的那些三角形。

每一个顶点都有自己的邻接三角形集合,用std::vector<int> 来存储这些三角形的索引,为此添加Mesh的成员AdjacentFacesPerVertex,类型为std::vector<std::vector<int>*>,含义就是所有点对应的邻接三角形索引集组成的集合。那如何从Mesh中求出所有点的邻接面呢?一个简单的思路就是对于给定Mesh中的点P,既然已知P在点集中的索引i,就遍历一遍三角形集合,凡是三角形的P0Index、P1Index、P2Index中有一个等于
i 则这个三角形就在P的邻接面集合里面。如果按这个思路,对于规模比较大的Mesh,要求出所有点的邻接面,就需要执行顶点数×三角形数×3的比较。这对于时间资源紧张的应用是不可接受的。所以一般这个问题是反过来解决的:遍历三角形集合,将这个三角形的索引直接添加到这个三角形的三个点的邻接面集合中去。这样只需要执行三角形数×3的操作,从数量级上减少了操作。相应的代码如下:
计算点法向
对于没有学过计算机图形学的人来讲点法向可能有点不太好理解。因为从立体几何的视角上看,一个点哪里来什么法向量?不过在计算机图形学中,点法向是用于渲染图形的很重要的量,它是有如下的定义:Mesh上一个点P的法向量为其邻接三角形法向量的均值,示意图如下:

点法向能较好贴合穿过该点处曲面的法线,因而采用点法向渲染的图像显得更为平滑。关于这些知识本文不过多介绍,这里只需求出点法向,那么就只需将此点处相邻三角形的面法向求出即可。也就是说在求点法向之前,要计算完面法向和邻接面。相应的代码如下:
计算邻接点
参考邻接面,邻接点也很容易理解,对于一个Mesh上的点V,其邻接点就是和他有一个三角形边相连的其他点。在下图用红点标出了点V的邻接点:
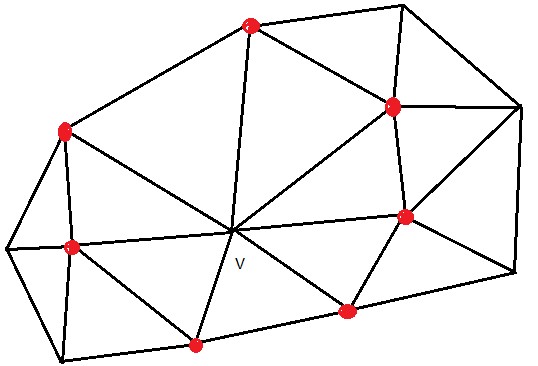
在邻接面的计算中,我们已经知道不应该采用对于每个点都遍历一遍三角形集合的方法来找想要的点。所以这里一样用到逆向的思维,只需遍历一次三角形表,对于每个三角形,P0的邻接点表添加P1、P2的索引;P1的邻接点表添加P0、P2的索引;P2的邻接点表添加P1,P0的索引。当然,由于同时有Pi Pj两个点的三角形往往不止一个,所以在添加的时候注意检测该点的索引是否已经被加进去了。
相应的代码如下:
拉普拉斯平滑
拉普拉斯平滑其实是对邻接点的一个简单应用。首先简单介绍一下网格的平滑。网格的平滑目的是使原本形状粗糙的网格表面变得更加光滑。如下图显示,左边模型经过平滑之后变成了右边较为平滑的模型。在Mesh平滑前后,只是顶点的位置发生改变,顶点之间的连接情况是不变的。

拉普拉斯平滑是网格平滑算法中最简单高效的一个,它的原理是将Mesh的每个顶点移到他邻接顶点的平均位置。所以此算法执行前首先要计算完邻接点。注意不能在一次循环中计算完某个点的平均位置后立刻修改该点的位置,因为这样会影响到后面顶点计算平均位置。所以算法采用和原点集相同大小的辅助空间来存放每个点将移到的新位置。所有点的新位置计算完成后再将这些位置的值覆盖修改原对应点的值。其原理用图表示如下:

注意平滑操作是可以反复迭代的,每迭代一次都是对所有的点计算一次位置,在迭代的过程中,Mesh也会越来越平滑。拉普拉斯平滑算法相应的代码如下:
最后本文完整的代码如下:
上篇文章讲述了一般的基本的Mesh应该至少包含点集和三角形集合的信息,也就是类似如下的定义方式:
struct Point3d
{
public:
float X;
float Y;
float Z;
Point3d()
{
X = 0;
Y = 0;
Z = 0;
}
~Point3d()
{
}
Point3d(float x, float y, float z)
{
this->X = x;
this->Y = y;
this->Z = z;
}
};
struct Triangle
{
public :
int P0Index;
int P1Index;
int P2Index;
Triangle(int p0index, int p1index, int p2index)
{
this->P0Index=p0index;
this->P1Index=p1index;
this->P2Index=p2index;
}
Triangle()
{
P0Index=-1;
P1Index=-1;
P2Index=-1;
}
};
class Mesh
{
public:
std::vector<Point3d> Vertices;
std::vector<Triangle> Faces;
int AddVertex(Point3d& toAdd)
{
int index = Vertices.size();
Vertices.push_back(toAdd);
return index;
}
int AddFace(Triangle& tri)
{
int index = Faces.size();
Faces.push_back(tri);
return index;
}
};本篇继续介绍Mesh相关的一些算法,包括计算面法向,邻接面,点法向,邻接点,以及拉普拉斯平滑算法,同时丰富了Mesh的成员。
计算面法向量
面法向量是Mesh中每一个三角形的法向量的集合,要得出这个集合,就应当为这个Mesh的每一个三角形计算法向量。注意,在立体几何中,一个面的法向量是方向垂直于这个面的向量(注意这里的向量都是指单位向量)。也就是说,对于一个面,这个面的法向量其实有两个方向,比如下图的平面。它的法向量既可以指向上面也可以指向下面。

但是对于Mesh中的三角形,法向量的方向是有讲究的,对于一个按P0、P1、P2顺序存储的三角形,它的法向量方向是符合右手法则的方向。就是用右手按P0、P1、P2的方向握过去,大拇指所指的方向,即下图的向上的向量,向下的向量是错误的。

区分法向量的方向是为了计算机图形的渲染,在渲染的时候,一般视法向量正对的方向为三角形的正面,而另一个相反的方向则是背面,在单侧光进行照射的时候,正面会根据材质进行适当的反光而显得明亮,而背面则暗淡一些。详细的关于光线照射这方面的信息,可以参考相应的书籍,本文就不再多述。
根据几何上对向量叉积的定义,面法向量可以使用三角形边向量的叉积计算:

为此特别定义向量Vector结构,同时在Mesh类中添加存储面法向的成员数组FaceNormals,类型为std::vector<Vector>,相应的代码如下:
struct Vector
{
public:
float X;
float Y;
float Z;
Vector()
{
X = 0;
Y = 0;
Z = 0;
}
~Vector()
{
}
Vector(float x, float y, float z)
{
this->X = x;
this->Y = y;
this->Z = z;
}
};Vector CaculateTriangleNormal(Point3d& p0, Point3d& p1, Point3d& p2)
{
Vector Normal;
float v1x = p1.X - p0.X;
float v1y = p1.Y - p0.Y;
float v1z = p1.Z - p0.Z;
float v2x = p2.X - p1.X;
float v2y = p2.Y - p1.Y;
float v2z = p2.Z - p1.Z;
Normal.X= v1y * v2z - v1z * v2y;
Normal.Y = v1z * v2x - v1x * v2z;
Normal.Z = v1x * v2y - v1y * v2x;
float len = (float)sqrt(Normal.X * Normal.X + Normal.Y * Normal.Y + Normal.Z * Normal.Z);
if (len == 0)
{
//throw Exception();
}
else
{
Normal.X /= len;
Normal.Y /= len;
Normal.Z /= len;
}
return Normal;
}void CaculateFaceNormals()
{
FaceNormals.reserve(Faces.size());
for(size_t i=0;i<Faces.size();i++)
{
Point3d& p0=Vertices[Faces[i].P0Index];
Point3d& p1=Vertices[Faces[i].P1Index];
Point3d& p2=Vertices[Faces[i].P2Index];
Vector v=CaculateTriangleNormal(p0,p1,p2);
FaceNormals.push_back(v);
}//对每一个三角形计算面法向并存至FaceNormals
}//计算面发向计算邻接面
求邻接面,或者说邻接三角形,简单的说就是对Mesh中的任何一个点,求出包含这个点的三角形的集合。如下图所示,对于点V而言,它的邻接面就是被标记为红色的那些三角形。

每一个顶点都有自己的邻接三角形集合,用std::vector<int> 来存储这些三角形的索引,为此添加Mesh的成员AdjacentFacesPerVertex,类型为std::vector<std::vector<int>*>,含义就是所有点对应的邻接三角形索引集组成的集合。那如何从Mesh中求出所有点的邻接面呢?一个简单的思路就是对于给定Mesh中的点P,既然已知P在点集中的索引i,就遍历一遍三角形集合,凡是三角形的P0Index、P1Index、P2Index中有一个等于
i 则这个三角形就在P的邻接面集合里面。如果按这个思路,对于规模比较大的Mesh,要求出所有点的邻接面,就需要执行顶点数×三角形数×3的比较。这对于时间资源紧张的应用是不可接受的。所以一般这个问题是反过来解决的:遍历三角形集合,将这个三角形的索引直接添加到这个三角形的三个点的邻接面集合中去。这样只需要执行三角形数×3的操作,从数量级上减少了操作。相应的代码如下:
void CaculateAdjacentFacesPerVertex()
{
AdjacentFacesPerVertex.reserve(Vertices.size());
for (size_t i = 0; i < Vertices.size(); i++)
{
std::vector<int>* list=new std::vector<int>();
list->reserve(4);//预先假设每个点大概有4个邻接面
AdjacentFacesPerVertex.push_back(list);
}//首先分配好存储空间
for (size_t i = 0; i < Faces.size(); i++)
{
Triangle& t = Faces[i];
std::vector<int> *t0list= AdjacentFacesPerVertex[t.P0Index];
std::vector<int> *t1list= AdjacentFacesPerVertex[t.P1Index];
std::vector<int> *t2list= AdjacentFacesPerVertex[t.P2Index];
t0list->push_back(i);
t1list->push_back(i);
t2list->push_back(i);
}//遍历三角形集合,使用三角形信息补充邻接面表
}//计算邻接面计算点法向
对于没有学过计算机图形学的人来讲点法向可能有点不太好理解。因为从立体几何的视角上看,一个点哪里来什么法向量?不过在计算机图形学中,点法向是用于渲染图形的很重要的量,它是有如下的定义:Mesh上一个点P的法向量为其邻接三角形法向量的均值,示意图如下:

点法向能较好贴合穿过该点处曲面的法线,因而采用点法向渲染的图像显得更为平滑。关于这些知识本文不过多介绍,这里只需求出点法向,那么就只需将此点处相邻三角形的面法向求出即可。也就是说在求点法向之前,要计算完面法向和邻接面。相应的代码如下:
void CaculateVertexNormals()
{
if(FaceNormals.size()==0)
CaculateFaceNormals();//计算点法向前需计算完面法向
if(AdjacentFacesPerVertex.size()==0)
CaculateAdjacentFacesPerVertex();//计算点法向前也必须计算完邻接面
VertexNormals.reserve(Vertices.size());
for (size_t i = 0; i < Vertices.size(); i++)
{
float sumx = 0;
float sumy = 0;
float sumz = 0;
std::vector<int>& tlist = *(AdjacentFacesPerVertex[i]);
if(tlist.size()!=0)
{
for (size_t j = 0; i < tlist.size(); j++)
{
sumx += FaceNormals[tlist[j]].X;
sumy += FaceNormals[tlist[j]].Y;
sumz += FaceNormals[tlist[j]].Z;
}
VertexNormals.push_back(Vector(sumx / tlist.size(), sumy / tlist.size(), sumz /tlist.size()));//求邻接面发向均值
}
else
{
VertexNormals.push_back(Vector(0,0,0));//若无邻接面,则为孤立点,使用默认值
}
}
}//计算点法向计算邻接点
参考邻接面,邻接点也很容易理解,对于一个Mesh上的点V,其邻接点就是和他有一个三角形边相连的其他点。在下图用红点标出了点V的邻接点:

在邻接面的计算中,我们已经知道不应该采用对于每个点都遍历一遍三角形集合的方法来找想要的点。所以这里一样用到逆向的思维,只需遍历一次三角形表,对于每个三角形,P0的邻接点表添加P1、P2的索引;P1的邻接点表添加P0、P2的索引;P2的邻接点表添加P1,P0的索引。当然,由于同时有Pi Pj两个点的三角形往往不止一个,所以在添加的时候注意检测该点的索引是否已经被加进去了。
相应的代码如下:
void CaculateAdjacentVerticesPerVertex()
{
AdjacentVerticesPerVertex.reserve(Vertices.size());
for (size_t i = 0; i < Vertices.size(); i++)
{
std::vector<int>* list=new std::vector<int>();
list->reserve(4);//预先假设每个点大概有4个邻接点
AdjacentVerticesPerVertex.push_back(list);
}//首先分配好存储空间
for (size_t i = 0; i < Faces.size(); i++)
{
Triangle &t = Faces[i];
std::vector<int> *p0list= AdjacentVerticesPerVertex[t.P0Index];
std::vector<int> *p1list= AdjacentVerticesPerVertex[t.P1Index];
std::vector<int> *p2list= AdjacentVerticesPerVertex[t.P2Index];
if (std::find(p0list->begin(), p0list->end(), t.P1Index)==p0list->end())
p0list->push_back(t.P1Index);
if (std::find(p0list->begin(), p0list->end(), t.P2Index)==p0list->end())
p0list->push_back(t.P2Index);
if (std::find(p1list->begin(), p1list->end(), t.P0Index)==p1list->end())
p1list->push_back(t.P0Index);
if (std::find(p1list->begin(), p1list->end(), t.P2Index)==p1list->end())
p1list->push_back(t.P2Index);
if (std::find(p2list->begin(), p2list->end(), t.P0Index)==p2list->end())
p2list->push_back(t.P0Index);
if (std::find(p2list->begin(), p2list->end(), t.P1Index)==p2list->end())
p2list->push_back(t.P1Index);
}//遍历三角形集合,使用三角形信息补充邻接面表
}//计算邻接点拉普拉斯平滑
拉普拉斯平滑其实是对邻接点的一个简单应用。首先简单介绍一下网格的平滑。网格的平滑目的是使原本形状粗糙的网格表面变得更加光滑。如下图显示,左边模型经过平滑之后变成了右边较为平滑的模型。在Mesh平滑前后,只是顶点的位置发生改变,顶点之间的连接情况是不变的。


拉普拉斯平滑是网格平滑算法中最简单高效的一个,它的原理是将Mesh的每个顶点移到他邻接顶点的平均位置。所以此算法执行前首先要计算完邻接点。注意不能在一次循环中计算完某个点的平均位置后立刻修改该点的位置,因为这样会影响到后面顶点计算平均位置。所以算法采用和原点集相同大小的辅助空间来存放每个点将移到的新位置。所有点的新位置计算完成后再将这些位置的值覆盖修改原对应点的值。其原理用图表示如下:

注意平滑操作是可以反复迭代的,每迭代一次都是对所有的点计算一次位置,在迭代的过程中,Mesh也会越来越平滑。拉普拉斯平滑算法相应的代码如下:
void LaplacianSmooth(int time)
{
if(AdjacentVerticesPerVertex.size()==0)
CaculateAdjacentVerticesPerVertex();//平滑前需要计算邻接点
Point3d* tempPos=new Point3d[Vertices.size()];//辅助空间存储每次平滑后的点将要挪到的位置
for(int k=0;k<time;k++)
{
for (size_t i = 0; i < Vertices.size(); i++)
{
float xav = 0;
float yav = 0;
float zav = 0;
std::vector<int>& adjlist =*(AdjacentVerticesPerVertex[i]);
size_t adjcount=adjlist.size();
if(adjcount==0)
continue;
for (size_t j = 0; j < adjcount; j++)
{
xav += Vertices[adjlist[j]].X;
yav += Vertices[adjlist[j]].Y;
zav += Vertices[adjlist[j]].Z;
}
xav /= adjcount;
yav /= adjcount;
zav /= adjcount;
tempPos[i].X = xav;
tempPos[i].Y = yav;
tempPos[i].Z = zav;
}//对所有点计算邻接点平均位置并存到辅助空间
for (size_t i = 0; i < Vertices.size(); i++)
{
Vertices[i].X = tempPos[i].X;
Vertices[i].Y = tempPos[i].Y;
Vertices[i].Z = tempPos[i].Z;
}//将计算出的新点位置覆盖原来点的位置
}//每次循环意味着一次平滑
delete[] tempPos;
}最后本文完整的代码如下:
#include <vector>
#include <algorithm>
struct Point3d
{
public:
float X;
float Y;
float Z;
Point3d()
{
X = 0;
Y = 0;
Z = 0;
}
~Point3d()
{
}
Point3d(float x, float y, float z)
{
this->X = x;
this->Y = y;
this->Z = z;
}
};
struct Triangle
{
public :
int P0Index;
int P1Index;
int P2Index;
Triangle(int p0index, int p1index, int p2index)
{
this->P0Index=p0index;
this->P1Index=p1index;
this->P2Index=p2index;
}
Triangle()
{
P0Index=-1;
P1Index=-1;
P2Index=-1;
}
};
struct Vector { public: float X; float Y; float Z; Vector() { X = 0; Y = 0; Z = 0; } ~Vector() { } Vector(float x, float y, float z) { this->X = x; this->Y = y; this->Z = z; } };
Vector CaculateTriangleNormal(Point3d& p0, Point3d& p1, Point3d& p2) { Vector Normal; float v1x = p1.X - p0.X; float v1y = p1.Y - p0.Y; float v1z = p1.Z - p0.Z; float v2x = p2.X - p1.X; float v2y = p2.Y - p1.Y; float v2z = p2.Z - p1.Z; Normal.X= v1y * v2z - v1z * v2y; Normal.Y = v1z * v2x - v1x * v2z; Normal.Z = v1x * v2y - v1y * v2x; float len = (float)sqrt(Normal.X * Normal.X + Normal.Y * Normal.Y + Normal.Z * Normal.Z); if (len == 0) { //throw Exception(); } else { Normal.X /= len; Normal.Y /= len; Normal.Z /= len; } return Normal; }
class Mesh
{
public:
std::vector<Point3d> Vertices;//存放点的集合
std::vector<Triangle> Faces;//存放三角形的集合
std::vector<Vector> FaceNormals;//存放面法向的集合,与三角形集合一一对应
std::vector<Vector> VertexNormals;//存放点法向的集合,与点集一一对应
std::vector<std::vector<int>*> AdjacentFacesPerVertex;//存放点的邻接面的集合,与点集一一对应
std::vector<std::vector<int>*> AdjacentVerticesPerVertex;//存放点的邻接点的集合,与点集一一对应
Mesh()
{
}
~Mesh()
{
}
int AddVertex(Point3d& toAdd)
{
int index = Vertices.size();
Vertices.push_back(toAdd);
return index;
}
int AddFace(Triangle& tri)
{
int index = Faces.size();
Faces.push_back(tri);
return index;
}
void CaculateFaceNormals() { FaceNormals.reserve(Faces.size()); for(size_t i=0;i<Faces.size();i++) { Point3d& p0=Vertices[Faces[i].P0Index]; Point3d& p1=Vertices[Faces[i].P1Index]; Point3d& p2=Vertices[Faces[i].P2Index]; Vector v=CaculateTriangleNormal(p0,p1,p2); FaceNormals.push_back(v); }//对每一个三角形计算面法向并存至FaceNormals }//计算面发向
void CaculateVertexNormals()
{
if(FaceNormals.size()==0)
CaculateFaceNormals();//计算点法向前需计算完面法向
if(AdjacentFacesPerVertex.size()==0)
CaculateAdjacentFacesPerVertex();//计算点法向前也必须计算完邻接面
VertexNormals.reserve(Vertices.size());
for (size_t i = 0; i < Vertices.size(); i++)
{
float sumx = 0;
float sumy = 0;
float sumz = 0;
std::vector<int>& tlist = *(AdjacentFacesPerVertex[i]);
if(tlist.size()!=0)
{
for (size_t j = 0; i < tlist.size(); j++)
{
sumx += FaceNormals[tlist[j]].X;
sumy += FaceNormals[tlist[j]].Y;
sumz += FaceNormals[tlist[j]].Z;
}
VertexNormals.push_back(Vector(sumx / tlist.size(), sumy / tlist.size(), sumz /tlist.size()));//求邻接面发向均值
}
else
{
VertexNormals.push_back(Vector(0,0,0));//若为孤立点则使用默认值
}
}
}//计算点法向
void CaculateAdjacentFacesPerVertex() { AdjacentFacesPerVertex.reserve(Vertices.size()); for (size_t i = 0; i < Vertices.size(); i++) { std::vector<int>* list=new std::vector<int>(); list->reserve(4);//预先假设每个点大概有4个邻接面 AdjacentFacesPerVertex.push_back(list); }//首先分配好存储空间 for (size_t i = 0; i < Faces.size(); i++) { Triangle& t = Faces[i]; std::vector<int> *t0list= AdjacentFacesPerVertex[t.P0Index]; std::vector<int> *t1list= AdjacentFacesPerVertex[t.P1Index]; std::vector<int> *t2list= AdjacentFacesPerVertex[t.P2Index]; t0list->push_back(i); t1list->push_back(i); t2list->push_back(i); }//遍历三角形集合,使用三角形信息补充邻接面表 }//计算邻接面
void CaculateAdjacentVerticesPerVertex() { AdjacentVerticesPerVertex.reserve(Vertices.size()); for (size_t i = 0; i < Vertices.size(); i++) { std::vector<int>* list=new std::vector<int>(); list->reserve(4);//预先假设每个点大概有4个邻接点 AdjacentVerticesPerVertex.push_back(list); }//首先分配好存储空间 for (size_t i = 0; i < Faces.size(); i++) { Triangle &t = Faces[i]; std::vector<int> *p0list= AdjacentVerticesPerVertex[t.P0Index]; std::vector<int> *p1list= AdjacentVerticesPerVertex[t.P1Index]; std::vector<int> *p2list= AdjacentVerticesPerVertex[t.P2Index]; if (std::find(p0list->begin(), p0list->end(), t.P1Index)==p0list->end()) p0list->push_back(t.P1Index); if (std::find(p0list->begin(), p0list->end(), t.P2Index)==p0list->end()) p0list->push_back(t.P2Index); if (std::find(p1list->begin(), p1list->end(), t.P0Index)==p1list->end()) p1list->push_back(t.P0Index); if (std::find(p1list->begin(), p1list->end(), t.P2Index)==p1list->end()) p1list->push_back(t.P2Index); if (std::find(p2list->begin(), p2list->end(), t.P0Index)==p2list->end()) p2list->push_back(t.P0Index); if (std::find(p2list->begin(), p2list->end(), t.P1Index)==p2list->end()) p2list->push_back(t.P1Index); }//遍历三角形集合,使用三角形信息补充邻接面表 }//计算邻接点
void LaplacianSmooth(int time) { if(AdjacentVerticesPerVertex.size()==0) CaculateAdjacentVerticesPerVertex();//平滑前需要计算邻接点 Point3d* tempPos=new Point3d[Vertices.size()];//辅助空间存储每次平滑后的点将要挪到的位置 for(int k=0;k<time;k++) { for (size_t i = 0; i < Vertices.size(); i++) { float xav = 0; float yav = 0; float zav = 0; std::vector<int>& adjlist =*(AdjacentVerticesPerVertex[i]); size_t adjcount=adjlist.size(); if(adjcount==0) continue; for (size_t j = 0; j < adjcount; j++) { xav += Vertices[adjlist[j]].X; yav += Vertices[adjlist[j]].Y; zav += Vertices[adjlist[j]].Z; } xav /= adjcount; yav /= adjcount; zav /= adjcount; tempPos[i].X = xav; tempPos[i].Y = yav; tempPos[i].Z = zav; }//对所有点计算邻接点平均位置并存到辅助空间 for (size_t i = 0; i < Vertices.size(); i++) { Vertices[i].X = tempPos[i].X; Vertices[i].Y = tempPos[i].Y; Vertices[i].Z = tempPos[i].Z; }//将计算出的新点位置覆盖原来点的位置 }//每次循环意味着一次平滑 delete[] tempPos; }
};
相关文章推荐
- 三角网格数据结构
- 数据结构和算法二叉树排序
- 数据结构第一讲
- 线性表--顺序实现
- 第9章 数据结构
- 第9章 数据结构
- 第9章 数据结构
- 【数据结构】树
- 数据结构实验之链表七:单链表中重复元素的删除
- 数据结构实验之链表六:有序链表的建立
- 数据结构之线性表的概念
- 数据结构实验之链表五:单链表的拆分
- 数据结构课程笔记_拓扑排序
- 关于数据结构的内存分配问题
- 使用JavaScript的数组实现数据结构中的队列与堆栈
- 共同学习Java源代码--数据结构--ArrayList类(四)
- SDUT3333数据结构实验之栈六:下一较大值(二)
- 数据结构实验之链表四:有序链表的归并
- 数据结构---链表操作(线性结构)
- 数据结构--链表的操作(顺序结构)
