几种数字仿真的物理意义与代码实现(二)
2016-05-16 22:29
549 查看
(四)增广矩阵:解决带有输入U(t)的数字仿真的问题。
以上数字积分法,梯形法与龙格库塔解决的问题中都是由y(0) ,y’来解决y(t) = e^(At)*y(0),也即是说根本没有出现输入U(t),但是实际的系统中都是有输入的,即使没有输入,也会有干扰,我们知道干扰可以当成一种变相的输入,所以我们要把输入考虑到系统内部。
这样一来,系统就变成了:X’ = AX + BU。我们只对简单的输入做处理。U(t)典型的也就是三种,即阶跃输入,斜坡输入,与指数输入。
只要把输入U考虑到原先的A矩阵中去,就可以将带有输入的系统变成龙格库塔能够处理的形式:X’ = AX。于是引入增广矩阵,就是把带有的U增广到状态变量中去,也就是把A矩阵进行增广。下面就是集中典型输入形式的增广A矩阵:
(1),阶跃输入:[X’(t); X’(t+1)] = [A B; 0 0]*[X(t) ;X(t+1)] 这时矩阵[A B; 0 0]就是增光后的矩阵,这里要注意下面补0要保证矩阵的合理性。
(2),斜坡输入: [X’(t); X’(t+1); X’(t+2)] = [A B 0; 0 0 1; 0 0 0]*[X(t) ;X(t+1) ;X(t+2)];增广矩阵为:[A B 0; 0 0 1; 0 0 0]
(3),指数输入:[X’(t); X’(t+1)] = [A B; 0 -1]*[X(t) ;X(t+1)] ,这时矩阵[A B; 0 -1]就是增光后的矩阵。
下面为实现与龙格库塔比较的代码:
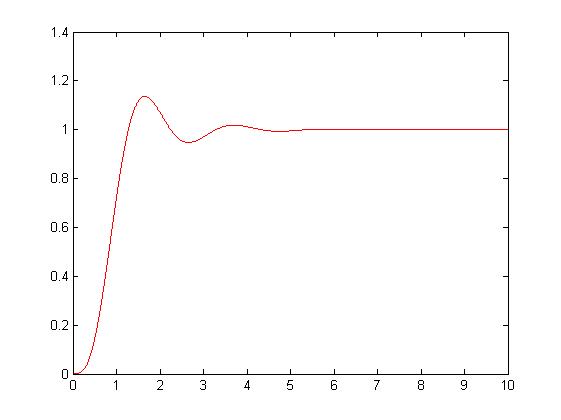
(五)亚当姆斯法:利用过去时刻的斜率进行推算下一时刻的值。
我们在利用前几种数字积分法的时候,都是需要计算几个时刻的斜率加以计算,但是我们已经得到的前面时刻的值,现在考虑将这些值都应用到下一时刻求解斜率上。我们利用这样的计算格式:
y(t+1) = y(t) + h*[(1-λ)y’(t) + λy’(t-1)].这样一来,我们就可以利用得已知的点的斜率来计算下一时刻的值。主要的问题就是怎么确定权重λ的值。同样,我们将y’(t-1)在y(t)时刻进行泰勒展开,然后代入到上式中在于y(t+1)在t时刻泰勒展开的公式进行一一对比,就可以推导得到二阶,三阶,或多阶的亚当姆斯法。
二阶: y(t+1) = y(t) + (h/2)(3y’ - y’(t-1))
三阶: y(t+1) = y(t) + (h/12)(23y’ - 16y’(t-1) + 5y’(t-2))
四阶: y(t+1) = y(t) + (h/24)(55y’ - 59y’(t-1) + 37y’(t-2) - 9y’(t-3))
(六)离散相似法:前面介绍的方法原理基本都相似,但是有一个最基本的bug:万一遇到了一个非线性的环节,例如:饱和环节,是不是就意味着后面的数据已经没有必要仿真了,饱和了!又或者遇到y = |t|,是不是就已经没有办法仿真了。由此引入处理非线性的数字仿真模型:先将信号进行离散化,再进行仿真。【这里说明:离散化的过程要采用保持器,保持器过程中已经进行了类似插值拟合,这样一来,非线性的数据已经进行了线性化的处理。】
(1),Z域的离散相似:如何连续系统是以传递函数表现出来的,这里无论传递韩素中是否含有非线性环节,都可以进行仿真。主要步骤很简单:将传递函数Z变换——>将变换后的传递函数X(z)与Y(z)分别写到左右——>再左右进行Z反变换就可以得到差分方程,下面就可以利用龙哥库塔方式进行计算了。
(2),时域的离散相似:使时域离散相似是是运用最多的数字仿真方法,它有着最大的优点:可以同时观测到几个环节的输入与输出变化趋势,即使最终的输出Y(t)为零,也可以有前面环节观测到系统的内部发生了什么。
已知,系统的状态方程X’ = AX + BU Y = CX +DU.
现在就看状态方程X’ = AX + BU将其进行拉普拉斯变换:sX(s) -X(0) = AX(s) + BU(s)
整理后再进行拉氏反变换的:X(t) = [exp(At)]X(0) + ∫exp(A(t-τ))BU(τ)dτ.然后分别带入KT与K(T+1)后再进行合并的最后的表达式:X[(k+1)T] = [exp(At)]X(kT) + ∫exp(A((k+1)T-τ))BU(τ)dτ
所以,表达式变成:X[(k+1)T] =phi*X(kT) + phi_m*U.只要能够求解出phi与phi_m,再结合链接矩阵[表示所有环节的输出与输入关系]就可以推导出来不同时刻各个环节的输入与输出。
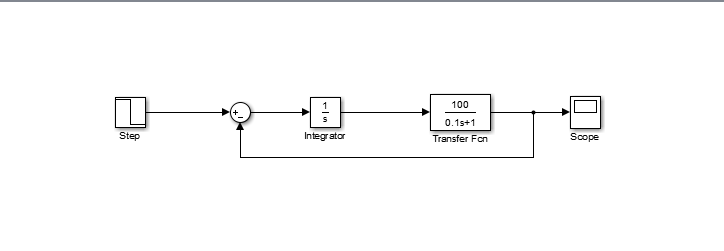
以下为离散相似的代码:
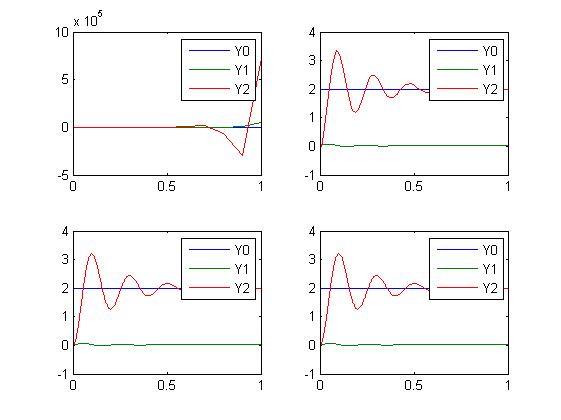
处理的结果(取不同的步长,显示的结果):
以上数字积分法,梯形法与龙格库塔解决的问题中都是由y(0) ,y’来解决y(t) = e^(At)*y(0),也即是说根本没有出现输入U(t),但是实际的系统中都是有输入的,即使没有输入,也会有干扰,我们知道干扰可以当成一种变相的输入,所以我们要把输入考虑到系统内部。
这样一来,系统就变成了:X’ = AX + BU。我们只对简单的输入做处理。U(t)典型的也就是三种,即阶跃输入,斜坡输入,与指数输入。
只要把输入U考虑到原先的A矩阵中去,就可以将带有输入的系统变成龙格库塔能够处理的形式:X’ = AX。于是引入增广矩阵,就是把带有的U增广到状态变量中去,也就是把A矩阵进行增广。下面就是集中典型输入形式的增广A矩阵:
(1),阶跃输入:[X’(t); X’(t+1)] = [A B; 0 0]*[X(t) ;X(t+1)] 这时矩阵[A B; 0 0]就是增光后的矩阵,这里要注意下面补0要保证矩阵的合理性。
(2),斜坡输入: [X’(t); X’(t+1); X’(t+2)] = [A B 0; 0 0 1; 0 0 0]*[X(t) ;X(t+1) ;X(t+2)];增广矩阵为:[A B 0; 0 0 1; 0 0 0]
(3),指数输入:[X’(t); X’(t+1)] = [A B; 0 -1]*[X(t) ;X(t+1)] ,这时矩阵[A B; 0 -1]就是增光后的矩阵。
下面为实现与龙格库塔比较的代码:
a=[1 0]; b=[1 4.6]; c=[1 3.4 16.35]; num=[5 100]; den=conv(a,conv(b,c)); den(4)=den(4)+num(1); den(5)=den(5)+num(2); sys_tf=tf(num,den) sys_ss=ss(sys_tf); [A,B,C,D]=ssdata(sys_ss) h=0.001; t=0:h:10; n=length(t); x=zeros(4,n); x(1,1)=0; x(2,1)=0; x(3,1)=0; x(4,1)=0; x0=[0;0;0;0]; A_2=[A B;0 0 0 0 0]; x_2=zeros(5,n); x_2(5,1)=1; for i=2:n; x_2(:,i)=(eye(5)+A_2*h+A_2^2*h^2/2+A_2^3*h^3/6+A_2^4*h^4/24)*x_2(:,i-1); end C_2=[C 0]; y_2=C_2*x_2; plot(t,y_2,'r')

(五)亚当姆斯法:利用过去时刻的斜率进行推算下一时刻的值。
我们在利用前几种数字积分法的时候,都是需要计算几个时刻的斜率加以计算,但是我们已经得到的前面时刻的值,现在考虑将这些值都应用到下一时刻求解斜率上。我们利用这样的计算格式:
y(t+1) = y(t) + h*[(1-λ)y’(t) + λy’(t-1)].这样一来,我们就可以利用得已知的点的斜率来计算下一时刻的值。主要的问题就是怎么确定权重λ的值。同样,我们将y’(t-1)在y(t)时刻进行泰勒展开,然后代入到上式中在于y(t+1)在t时刻泰勒展开的公式进行一一对比,就可以推导得到二阶,三阶,或多阶的亚当姆斯法。
二阶: y(t+1) = y(t) + (h/2)(3y’ - y’(t-1))
三阶: y(t+1) = y(t) + (h/12)(23y’ - 16y’(t-1) + 5y’(t-2))
四阶: y(t+1) = y(t) + (h/24)(55y’ - 59y’(t-1) + 37y’(t-2) - 9y’(t-3))
(六)离散相似法:前面介绍的方法原理基本都相似,但是有一个最基本的bug:万一遇到了一个非线性的环节,例如:饱和环节,是不是就意味着后面的数据已经没有必要仿真了,饱和了!又或者遇到y = |t|,是不是就已经没有办法仿真了。由此引入处理非线性的数字仿真模型:先将信号进行离散化,再进行仿真。【这里说明:离散化的过程要采用保持器,保持器过程中已经进行了类似插值拟合,这样一来,非线性的数据已经进行了线性化的处理。】
(1),Z域的离散相似:如何连续系统是以传递函数表现出来的,这里无论传递韩素中是否含有非线性环节,都可以进行仿真。主要步骤很简单:将传递函数Z变换——>将变换后的传递函数X(z)与Y(z)分别写到左右——>再左右进行Z反变换就可以得到差分方程,下面就可以利用龙哥库塔方式进行计算了。
(2),时域的离散相似:使时域离散相似是是运用最多的数字仿真方法,它有着最大的优点:可以同时观测到几个环节的输入与输出变化趋势,即使最终的输出Y(t)为零,也可以有前面环节观测到系统的内部发生了什么。
已知,系统的状态方程X’ = AX + BU Y = CX +DU.
现在就看状态方程X’ = AX + BU将其进行拉普拉斯变换:sX(s) -X(0) = AX(s) + BU(s)
整理后再进行拉氏反变换的:X(t) = [exp(At)]X(0) + ∫exp(A(t-τ))BU(τ)dτ.然后分别带入KT与K(T+1)后再进行合并的最后的表达式:X[(k+1)T] = [exp(At)]X(kT) + ∫exp(A((k+1)T-τ))BU(τ)dτ
所以,表达式变成:X[(k+1)T] =phi*X(kT) + phi_m*U.只要能够求解出phi与phi_m,再结合链接矩阵[表示所有环节的输出与输入关系]就可以推导出来不同时刻各个环节的输入与输出。

以下为离散相似的代码:
for j=1:4
h=10^-j;
T=1;
t=0:h:T;
N=length(t);
num1=[1];
den1=[1,0];
num2=[100];
den2=[0.1,1];
[A1,B1,C1,D1]=tf2ss(num1,den1);
[A2,B2,C2,D2]=tf2ss(num2,den2);
[phi_1,phi_m_1,phi_mm_1]=para(A1,B1,h);
[phi_2,phi_m_2,phi_mm_2]=para(A2,B2,h);
W=[1,0,-1;0,1,0];
Y=[2*ones(1,N);zeros(1,N);zeros(1,N)];
X=zeros(2,N);
U=zeros(2,N);
U(:,1)=[2,0];
Ub=[0,0]';
for i=1:N-1
U(:,i)=W*Y(:,i);
U(:,i+1)=2*U(:,i)-Ub;
Ub=U(:,i);
X(1,i+1)=phi_1*X(1,i)+phi_m_1*U(1,i)+phi_mm_1*(U(1,i+1)-U(1,i))/h;
X(2,i+1)=phi_2*X(2,i)+phi_m_2*U(2,i)+phi_mm_2*(U(2,i+1)-U(2,i))/h;
Y(2,i+1)=C1*X(1,i+1)+D1*U(1,i+1);
Y(3,i+1)=C2*X(2,i+1)+D2*U(2,i+1);
end
subplot(2,2,j)
plot(t,Y)
legend('Y0','Y1','Y2')
end处理的结果(取不同的步长,显示的结果):

相关文章推荐
- 解析在main函数之前调用函数以及对设计的作用详解
- 详解Matlab中 sort 函数用法
- java和matlab画多边形闭合折线图示例讲解
- C#调用Matlab生成的dll方法的详细说明
- 简述Matlab中size()函数的用法
- 从java中调用matlab详细介绍
- 稀疏自动编码器 (Sparse Autoencoder)
- 详解Matlab中 sort 函数用法
- 简述Matlab中size()函数的用法
- VC++与Matlab混合编程的快速实现
- Matlab 矩阵运算
- matlab与opencv部分函数的对照
- matlab神经网络工具箱创建神经网络
- Matlab
- MATLAB 入门教程
- matlab函数_连通区域
- MATLAB中函数模式和命令模式的区别
- MATLAB 添加自定义的模块到simulink库浏览器
- Export Figures for LaTeX Writing
