网络流建模学习笔记

题目来源：《网络流建模汇总》 by Edelweiss 很好的学习资料，尽管题型并不全面（个人以为），但是有很多新的idea，推荐一下。

1.分析题目的限制

POJ 1149 PIGS

有 M 个猪圈，每个猪圈里初始时有若干头猪。一开始所有猪圈都是关闭的。依 次来了 N个顾客，每个顾客分别会打开指定的几个猪圈，从中买若干头猪。每 个顾客分别都有他能够买的数量的上限。每个顾客走后，他打开的那些猪圈中的猪，都可以被任意地调换到其它开着的猪圈里，然后所有猪圈重新关上。问总共 最多能卖出多少头猪。（1 <= N <= 100, 1 <= M <= 1000）

这道题里面猪很显然是流，人和猪圈设成点。但是题目的限制很奇妙：打开过的猪圈里的猪能跑，没有打开的不能跑。

所以简单的把人和猪圈弄成二分图显然不行 所以需要拆点 把选择的顺序考虑进去。

思路见原文 不过优化方法很值得借鉴。

2.网络流love二分

一些限制条件可以通过二分判断是否满流解决。

POJ 2391 Ombrophobic Bovines

给定一个无向图，点 i 处有 Ai 头牛，点 i 处的牛棚能容纳 Bi 头牛，每条边都有通过的时间，求一个最短时 间 T 使得在 T 时间内所有的牛都能进到某一牛棚里去。（1 <= N <= 200, 1 <= M <= 1500, 0 <= Ai <= 1000, 0 <= Bi <= 1000, 1 <= Dij <= 1,000,000,000）

时间不是流量，也不是费用，却是可达性的限制 所以只需要二分答案加边，判断能否满流即可。

SGU 438 The Glorious Karlutka River =)

有一条东西向流淌的河，宽为 W，河中有 N 块石头，每块石头的坐标(Xi, Yi)和最 大承受人数 Ci 已知。现在有 M 个游客在河的南岸，他们想穿越这条河流，但是 每个人每次最远只能跳 D 米，每跳一次耗时 1 秒。问他们能否全部穿越这条河 流，如果能，最少需要多长时间。 （0 <= N <= 50, 0 < M <= 50, 0 <= D <= 1000, 0 < W <= 1000, 0 < Xi < 1000, 0 < Yi < W, 0 <= Ci <= 1000）

答案不是简单的最大流或最小费用问题，而是询问距离的上界。

距离也不是最大流问题本身的优化目标，所以要通过二分或枚举确定界限，动态加边，然后转化为了判定问题：能否让所有人通过。

3.网络流love竞赛图

POJ 2699 The Maximum Number of Strong Kings

一场联赛可以表示成一个完全图，点表示参赛选手，任意两点 u, v 之间有且仅有 一条有向边(u, v)或(v, u)，表示 u 打败 v 或 v 打败 u。一个选手的得分等于被他打 败的选手总数。一个选手被称为“strong king”当且仅当他打败了所有比他分高 的选手。分数最高的选手也是 strong king。现在给出某场联赛所有选手的得分序 列，由低到高，问合理安排每场比赛的结果后最多能有几个 strong king。已知选 手总数不超过 10 个。

看上去好复杂的样子，最优化目标不容易求

由于选手数字少，转而考虑枚举，判断是否可行。枚举集合还是个数呢？前者比后者容易（当然也不如后者优），不妨先尝试后者。

让谁承担充当strong king任务呢？随便选择吗？当然是获胜场数尽量多的人承担。

Question：会不会有这样一个Strong King甲，有一个普通人乙得分比他高呢？

Answer：感觉看上去有可能，事实上确实存在反例，不妨找一找试一试——



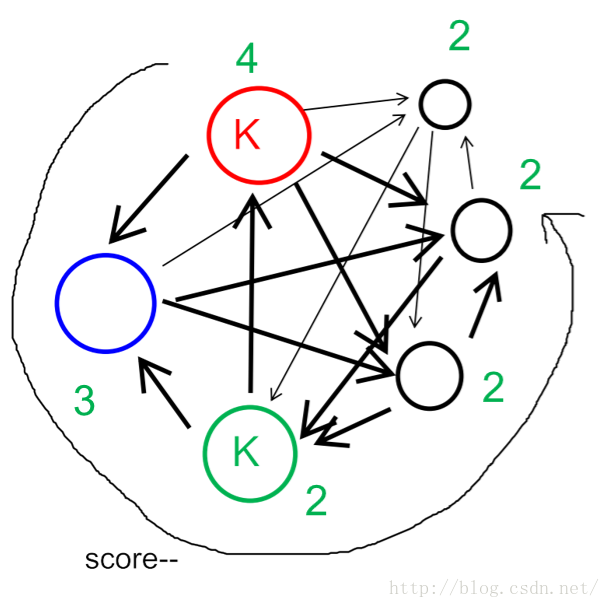
确实，对于一个分数不增的序列来说，他的SK(Strong King)真不一定连在一起

但是！题目只是要求合理安排！我们只要能把得分最高的都弄成SK就可以了！这只是说明上面的安排并不合理！

如果绿点能当SK，那么在一定有一种方案中蓝色是SK。绿色当SK要战胜的对手设为a，蓝色只需战胜a-1个对手；蓝色得分x，绿色得分为y，且y<x。只要a−1≤x就存在这样一个方案，要推翻蓝色不能成为SK的结论，必须假设a−1>x，这样a>a−1>y，绿色更不可能战胜所有对手。（如果把读者绕晕了，本菜很抱歉）

接下来，让SK之间的比赛定向（从分低到高），问题只需要找到方案能安排剩余的方向满足题意即可。

下面是竞赛图的常见建模方法：

1.对每一场比赛建点i， 连边(s, i) 容量1

2.比赛i到选手j（2个）各自连边(i, j) 容量1

3.选手到汇点连边，容量为要求获胜场数，这样判断是否满流即可

在其他题目中，如《WOJ 1124 Football Coach》，建模方法大同小异，只是连边的容量会发生变化（根据题目要求来）

4.建立s-t流与实际意义之间的关系

SPOJ 287 Smart Network Administrator

一座村庄有 N 户人家。只有第一家可以连上互联网，其他人家要想上网必须拉 一根缆线通过若干条街道连到第一家。每一根完整的缆线只能有一种颜色。网管 有一个要求，各条街道内不同人家的缆线必须不同色，且总的不同颜色种数最小。 求在指定的 K 户人家都能上网的前提下，最小的不同颜色种数。（1 <= N <= 500）

如果把同色的电缆都看成同一条s-t流，那岂不是s-t流要在网络里转好几个圈才能出来？这并不是距离最短的路线，一定还可以增广。

开阔一下思路：颜色种数肯定不小于同一条边上最大的颜色数，而且最佳情况下不超过该颜色数（？）这次仍然是只需要存在这样一个方案即可。

所以答案成了流量限制。跑一遍最大流，如果最大流量正好等于家庭数，那么流量限制可行，就可以对流量限制二分。非常幸运，这样做结果都是对的。

容易看出颜色数≤最大边权，但是我还没有证明等号一定成立。下面我试着证明一下。不想看证明的话可以自行跳过。

采用反证法，先假设最大边权为c-1是可行的（即能够满流），但是颜色数不能小于c。

假如这个图存在桥，割断后把图分成两个连通分量，那么这座桥一定满流，也就是说容量是c-1。在桥上只用到了c-1种颜色，再拉一条电缆，就会使流量超过上界，不符合可行流的性质。

那么，既然图中不会有桥，就一定存在两条不相交路径。两条路径上一定各自有一条边满流。只要让两条路径上各自拉一条同色的电缆，然后每条路径上就只剩下c-2条电缆可以拉，假如各使用不同颜色，那么可以获得一个总色数不超过c-1的方案。又与假设矛盾了。

假如这样的路径很多，会不会相互影响？不会的，我们对每种颜色编号，根据上面的证明，只会用到c-1种编号。这就完成了证明。

5.有下界的一般建模办法

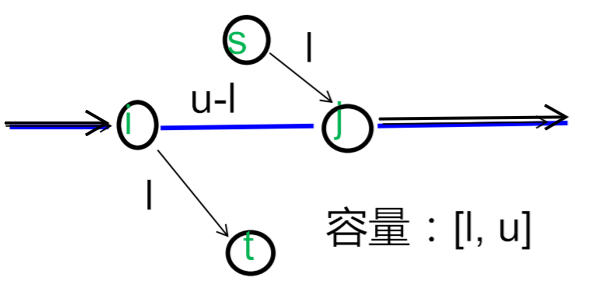
这一个非常具有一般性：对于每条下界大于0的边(i, j), 连边

1.(i, t)，容量为下界l

2.(s, j)，容量为下界l

3.(i, j)本身，容量为上界u-下界l（没有上界？那么容量是∞）

如果规定顶点容量下界，就拆点之后照上面处理



下界流量好像“搭着便车”一样流走了，这条边变成了我们熟悉的下界为0的模型。注意判断新增的两条边是否满流，如果不满流，就不存在可行方案。

这样转化之后许多题目不好直接转化为最大流，但可以找到流量下界都可以迎刃而解，比如最小权路径覆盖问题（ZJOI营救皮卡丘），还有NOI2008志愿者招募。

6.灵活应用流量守恒

算法导论上用线性规划形式化地表达了最大流问题的数学模型：

最大化：∑v∈Vfsv−∑v∈Vfvs

约束条件：fuv≤c(u,v)∀u,v∈V

∑u∈Vfuv=∑v∈Vfvu∀u∈V−{s,t}

fuv≥0

看起来玄之又玄……

这里的f是一个流量的函数，可以单纯地把fuv理解为(u, v)上的实际流量。c(u, v)就是容量。V是图中顶点的集合。最大化的函数是指流出源点的净流量（因为会有反向弧），在具体问题中会代表一系列最优化的自变量值。约束条件里最有价值的是第二条：只有它是一个等式。举个例子，NOI2008志愿者的神构图就来自于流量守恒。再有经典的问题：混合图中确定一条欧拉回路，也可以用流量守恒模型容易地解释。

对于欧拉回路，入度=出度，或者更形式一点：∑u∈V[(u,x)∈E]=∑v∈x[(x,v)∈E]

观察到和上面第二个式子很相像了。如何去寻找这一种方案呢？无向边还没定向，不妨先随意定向。如果出度大于入度，就需要从源点向这个点连边补充流量；否则反之。这样，一旦所有的边都满流，新图由于流量守恒的限制，一定符合题意。

这里只给出概念性描述（真相是我也有点忘了-_-|||），自行百度吧哈哈哈

后记

这些是我个人的学习体会、疑惑、总结，有点像写日记，有些地方不那么严谨。如果大神觉得不合适，想喷的话，我只能说：轻点儿~

finished in 2016.4.28