随机数https://en.wikipedia.org/wiki/Linear_congruential_generator

Linear congruential generator

From Wikipedia, the free encyclopedia








Visualisation of generation of pseudo-random numbers in [0, 8] using a linear congruential generator. The top two rows show a generator with m = 9, a = 2 and c = 0 outputting numbers from left to right until the output equals the seed, when the sequence repeats.
A seed of 1 gives a cycle length of 6 but a seed of 3 gives a cycle length of only 2. Using a = 4 and c = 1 (bottom row) gives a full cycle length of 9 with any seed.

A linear congruential generator (LCG) is an algorithm that
yields a sequence of pseudo-randomized numbers calculated with a discontinuouspiecewise
linear equation. The method represents one of the oldest and best-known pseudorandom
number generator algorithms.[1] The
theory behind them is relatively easy to understand, and they are easily implemented and fast, especially on computer hardware which can provide modulo
arithmetic by storage-bit truncation.
The generator is defined by the recurrence
relation:



where

is
the sequence of pseudorandom values, and


– the "modulus"

–
the "multiplier"

–
the "increment"

–
the "seed" or "start value"
are integer constants that specify the
generator. If c = 0, the generator is often called a multiplicative congruential generator (MCG), or Lehmer
RNG. If c ≠ 0, the method is called a mixed congruential generator.[2]

Contents

[hide]

1Period
length
2Parameters
in common use
3Advantages
and disadvantages of LCGs
4Comparison
with other PRNGs
5See
also
6Notes
7References
8External
links

Period length[edit]

The period of a
general LCG is at most m, and for some choices of factor a much less than that. The LCG will have a full period for all seed valuesif
and only if:[2]:17-19


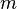
and the offset

are relatively
prime,


is divisible by
all prime factors of

,


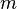
is divisible by
4 if

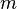
is divisible by 4.

These three requirements are referred to as the Hull-Dobell Theorem.[3] While
LCGs are capable of producing pseudorandom numbers which can
pass formaltests for randomness, this is extremely sensitive
to the choice of the parameters c, m, and a.
Historically, poor choices had led to ineffective implementations of LCGs. A particularly illustrative example of this is RANDU,
which was widely used in the early 1970s and led to many results which are currently being questioned because of the use of this poor LCG.[4]

Parameters in common use[edit]

The most efficient LCGs have an m equal to a power of 2, most often m = 232 or m = 264,
because this allows the modulus operation to be computed by merely truncating all but the rightmost 32 or 64 bits. The following table lists the parameters of LCGs in common use, including built-in rand()functions in runtime
libraries of various compilers.

Source	m	(multiplier) a	(increment) c	output bits of seed in rand() /Random(L)
Numerical Recipes	232	1664525	1013904223
Borland C/C++	232	22695477	1	bits 30..16 in rand(), 30..0 inlrand()
glibc (used by GCC)[5]	231	1103515245	12345	bits 30..0
ANSI C: Watcom, Digital Mars, CodeWarrior, IBM VisualAgeC/C++ [6]	231	1103515245	12345	bits 30..16
C99, C11: Suggestion in the ISO/IEC 9899 [7]	232	1103515245	12345	bits 30..16
Borland Delphi, Virtual Pascal	232	134775813	1	bits 63..32 of (seed * L)
Microsoft Visual/Quick C/C++	232	214013 (343FD16)	2531011 (269EC316)	bits 30..16
Microsoft Visual Basic (6 and earlier)[8]	224	1140671485 (43FD43FD16)	12820163 (C39EC316)
RtlUniform from Native API[9]	231 − 1	2147483629 (7FFFFFED16)	2147483587 (7FFFFFC316)
Apple CarbonLib, C++11's minstd_rand0 [10]	231 − 1	16807	0	see MINSTD
C++11's minstd_rand [10]	231 − 1	48271	0	see MINSTD
MMIX by Donald Knuth	264	6364136223846793005	1442695040888963407
Newlib, Musl	264	6364136223846793005	1	bits 63...32
VMS's MTH$RANDOM,[11] old versions of glibc	232	69069	1
Java's java.util.Random, POSIX [ln]rand48, glibc[ln]rand48[_r]	248	25214903917 (5DEECE66D16)	11	bits 47...16
POSIX[12] [jm]rand48, glibc [mj]rand48[_r]	248	25214903917 (5DEECE66D16)	11	bits 47...15
POSIX [de]rand48, glibc [de]rand48[_r]	248	25214903917 (5DEECE66D16)	11	bits 47...0
Formerly common: RANDU [4]	231	65539	0

As shown above, LCGs do not always use all of the bits in the values they produce. For example, the Java implementation
operates with 48-bit values at each iteration but returns only their 32 most significant bits. This is because the higher-order bits have longer periods than the lower-order bits (see below). LCGs that use this truncation technique produce statistically better
values than those that do not.
The Knuth representation for 3 variables is as below: Xn+1 = (8121 Xn +
28411) mod 134456
Because there are only 134456 distinct possible values, according to the parameter definition, it tends to make it a bit more predictable. If Xn is
even then Xn+1 will be odd, and vice versa, so the lowest order of bit oscillates at each step. This makes the generator to produce bits in each number that are usually not equally random.

Advantages and disadvantages of LCGs[edit]

LCGs are fast and require minimal memory (typically 32 or 64 bits) to retain state. This makes them valuable for simulating multiple independent streams.






Hyperplanes of a linear congruential generator in three dimensions

LCGs should not be used for applications where high-quality randomness is
critical. For example, it is not suitable for a Monte Carlo
simulation because of the serial correlation (among other things).
They also must not be used for cryptographic applications; see cryptographically
secure pseudo-random number generator for more suitable generators. If a linear congruential generator is seeded with a character and then iterated once, the result is a simple classical cipher called an affine
cipher; this cipher is easily broken by standard frequency analysis.
LCGs tend to exhibit some severe defects. For instance, if an LCG is used to choose points in an n-dimensional space, the points will lie on, at most, (n!m)1/n hyperplanes (Marsaglia's
Theorem, developed by George Marsaglia). This is due to serial correlation between
successive values of the sequence Xn. The spectral
test, which is a simple test of an LCG's quality, is based on this fact.
A further problem of LCGs is that the lower-order bits of the generated sequence have a far shorter period than the sequence as a whole if m is set to a power
of 2. In general, the nth least significant digit in the base brepresentation of the output sequence, where bk = m for some integer k, repeats with at
most period bn.
Yet another problem is that LCGs are not suitable for parallel programming. Multiple threads may access the currently stored state simultaneously causing a race condition. In implementations
which use same initialization for different threads, equal sequences of random numbers may occur on simultaneously executing threads. Random number generators, particularly for parallel computers, should not be trusted.[13] It
is strongly recommended to check the results of simulation with more than one RNG to check if bias is introduced. Among the recommended generators for use on a parallel computer include combined linear congruential generators using sequence splitting and lagged
Fibonacci generators using independent sequences.[13]
Nevertheless, for some applications LCGs may be a good option. For instance, in an embedded system, the amount of memory available is often severely limited. Similarly, in an environment
such as a video game console taking a small number of high-order bits of an LCG may
well suffice. The low-order bits of LCGs when m is a power of 2 should never be relied on for any degree of randomness whatsoever. Indeed, simply substituting 2n for the modulus term reveals that the
low order bits go through very short cycles. In particular, any full-cycle LCG when m is a power of 2 will produce alternately odd and even results.

Comparison with other PRNGs[edit]

If higher-quality random numbers are needed, and sufficient memory is available (~ 2 kilobytes),
then the Mersenne twister algorithm provides a vastly longer period
(219937 − 1) and variate uniformity.[14] A
common Mersenne twister implementation, interestingly enough, uses an LCG to generate seed data.
Linear congruential generators have the problem that all of the bits in each number are usually not equally random. A linear
feedback shift registerPRNG produces a stream of pseudo-random bits, each of which are truly pseudo-random,[15] and
can be implemented with essentially the same amount of memory as a linear congruential generator, albeit with a bit more computation.
The linear feedback shift register has a strong relationship to linear congruential generators.[16] Given
a few values in the sequence, some techniques can predict the following values in the sequence for not only linear congruent generators but any other polynomial congruent generator.[16]

See also[edit]

Full cycle
Inversive congruential generator
Multiply-with-carry
Lehmer RNG (sometimes called the Park-Miller RNG)
Combined Linear
Congruential Generator

Notes[edit]

Jump
up^ "Linear
Congruential Generators" by Joe Bolte, Wolfram Demonstrations
Project.
^ Jump
up to:a b Donald
E. Knuth (6 May 2014). Art of Computer Programming, Volume 2: Seminumerical
Algorithms. Addison-Wesley Professional. pp. 4–.ISBN 978-0-321-63576-1.
Jump
up^ Severance, Frank (2001). System Modeling and Simulation. John Wiley & Sons, Ltd. p. 86. ISBN 0-471-49694-4.
^ Jump
up to:a b Press,
William H.; et al. (1992). Numerical Recipes in Fortran 77: The Art of Scientific
Computing (2nd ed.). ISBN 0-521-43064-X.
Jump
up^ The GNU C library's rand() in stdlib.h uses
a simple (single state) linear congruential generator only in case that the state is declared as 8 bytes. If the state is larger (an array), the generator becomes an additive feedback generator and the period increases. See the simplified
code that reproduces the random sequence from this library.
Jump
up^ "A
collection of selected pseudorandom number generators with linear structures, K. Entacher, 1997". Retrieved 16 June 2012.
Jump
up^ "Last
public Committee Draft from April 12, 2011, page 346f" (PDF). Retrieved 21 Dec 2014.
Jump
up^ "How
Visual Basic Generates Pseudo-Random Numbers for the RND Function". Microsoft Support. Microsoft. Retrieved 17 June 2011.
Jump
up^ In spite of documentation on MSDN,
RtlUniform uses LCG, and not Lehmer's algorithm, implementations before Windows Vista are flawed,
because the result of multiplication is cut to 32 bits, before modulo is applied
^ Jump
up to:a b "ISO/IEC
14882:2011". ISO. 2 September 2011. Retrieved 3 September2011.
Jump
up^ GNU
Scientific Library: Other random number generators
Jump
up^ The Open Group
Base Specifications Issue 7 IEEE Std 1003.1, 2013 Edition
^ Jump
up to:a b Coddington,
Paul D. "Random number generators for parallel computers." (1997).
Jump
up^ Matsumoto, Makoto, and Takuji Nishimura (1998) ACM Transactions on Modeling and Computer Simulation 8
Jump
up^ * Neil Gershenfeld. The
Nature of Mathematical Modeling, First Edition. Cambridge University Press, 1999. ISBN
0-521-57095-6. Section 5.3.2: Linear Feedback, p. 59.
^ Jump
up to:a b RFC
4086 section 6.1.3 "Traditional Pseudo-random Sequences"

References[edit]

S.K. Park and K.W. Miller (1988). "Random
Number Generators: Good Ones Are Hard To Find". Communications of
the ACM 31 (10): 1192–1201.doi:10.1145/63039.63042.
D. E. Knuth. The Art of Computer Programming, Volume 2: Seminumerical
Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89684-2.
Section 3.2.1: The Linear Congruential Method, pp. 10–26.
P. L'Ecuyer (1999). "Tables
of Linear Congruential Generators of Different Sizes and Good Lattice Structure". Mathematics
of Computation 68(225): 249–260. doi:10.1090/S0025-5718-99-00996-5.
Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section
7.1.1. Some History", Numerical Recipes: The Art of Scientific Computing(3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
Gentle, James E., (2003). Random Number Generation and Monte Carlo Methods, 2nd edition, Springer, ISBN
0-387-00178-6.
Joan Boyar (1989). "Inferring
sequences produced by pseudo-random number generators". Journal of the ACM 36 (1):
129–141.doi:10.1145/58562.59305. (in
this paper, efficient algorithms are given for inferring sequences produced by certain pseudo-random number generators).

External links[edit]

The simulation Linear Congruential Generator visualizes
the correlations between the pseudo-random numbers when manipulating the parameters.
Security of Random Number Generation: An
Annotated Bibliography
Linear Congruential Generators post to sci.math
The "Death of Art" computer art project at Goldstein
Technologies LLC, uses an LCG to generate 33,554,432 images
P. L'Ecuyer and R. Simard, "TestU01:
A C Library for Empirical Testing of Random Number Generators", May 2006, revised November 2006, ACM Transactions on Mathematical Software, 33, 4, Article 22, August 2007.
Article about another way of cracking LCG

Categories:

Pseudorandom number generators

Modular arithmetic

Navigation menu

Create
account

Not logged in

Talk

Contributions

Log
in

Article

Talk

Read

Edit

View
history



Main page

Contents

Featured content

Current events

Random article

Donate
to Wikipedia

Wikipedia store

Interaction

Help

About Wikipedia

Community portal

Recent changes

Contact page

Tools

What
links here

Related
changes

Upload file

Special pages

Permanent link

Page information

Wikidata item

Cite this
page

Print/export

Create a book

Download
as PDF

Printable
version

Languages

Čeština

Deutsch

Français

한국어

Հայերեն

Italiano

Nederlands

日本語

Русский

Svenska

ไทย

中文

Edit
links

This page was last modified on 24 November 2015, at 16:09.

Text is available under the Creative Commons
Attribution-ShareAlike License; additional terms may apply. By using this site, you agree to the Terms of Use and Privacy
Policy. Wikipedia® is a registered trademark of the Wikimedia Foundation, Inc., a non-profit organiza