欧拉路的判定 http://hihocoder.com/problemset/problem/1176

http://hihocoder.com/problemset/problem/1176

小Ho：好麻烦啊，是我的话就随便走几步，到没路可走不就好了么！ 小Hi：那样的话，收集的道具会少很多，万一以后要用到，又得重新读档了。
小Ho：好吧，让我先想想。
<两分钟后>
小Ho：这个好像是一笔画问题哎，我们是在求一个方法能够一笔画出所有边吧?
小Hi：没错，这就是一笔画问题，不过它更正式的名字叫做欧拉路问题。其定义是
给定无孤立结点图G，若存在一条路，经过图中每边一次且仅一次，该条路称为欧拉路。
小Ho：既然有名字，那就证明这东西有解咯？
小Hi：没错，欧拉路是有判定条件的：一个无向图存在欧拉路当且仅当该图是连通的且有且只有2个点的度数是奇数，此时这两个点只能作为欧拉路径的起点和终点。
若图中没有奇数度的点，那么起点和终点一定是同一个点，这样的欧拉路叫做欧拉回路
对于任意一个点来说，从其他点到它的次数和从它到其他点的次数必然是相等的，否则就会出现出去次数和进入次数不同。若进入次数多，则该点位终点，若出去次数多则该点为起点。
对于一个无向图来说，进入和出去的次数恰好反映在度的数量上。所以奇数度的点至多只能有2个。
严格的证明的话：
若图G连通，有零个或两个奇数度结点，我们总有如下方法构造一条欧拉路：

若有两个奇数度结点，则从其中的一个结点开始构造一条迹，即从v[0]出发经关联边e[1]“进入”v[1]，若v[1]的度数为偶数，则必可由v[1]再经关联边e[2]进入v[2]，如此进行下去，每边仅取一次。由于G是连通的，故必可到达另一奇数度结点停下，得到一条迹L：v[0]-e[1]-v[1]-e[2]…v[i]-e[i+1]…v[k]。若G中没有奇数度结点则从任一结点v[0]出发，用上述方法必可回到结点v[0]，得到上述一条闭迹L1。
若L1通过了G的所有边，则L1就是欧拉路。
若G中去掉L1后得到子图G′，则G′中每个结点度数为偶数，因为原来的图是连通的，故L1与G′至少有一个结点v[i]重合，在G′中由v[i]出发重复第一步的方法，得到闭迹L2。
当L1与L2组合在一起，如果恰是G，则即得欧拉路，否则重复第三步可得到闭迹L3，以此类推直到得到一条经过图G中所有边的欧拉路。

不妨看看前面的例子：



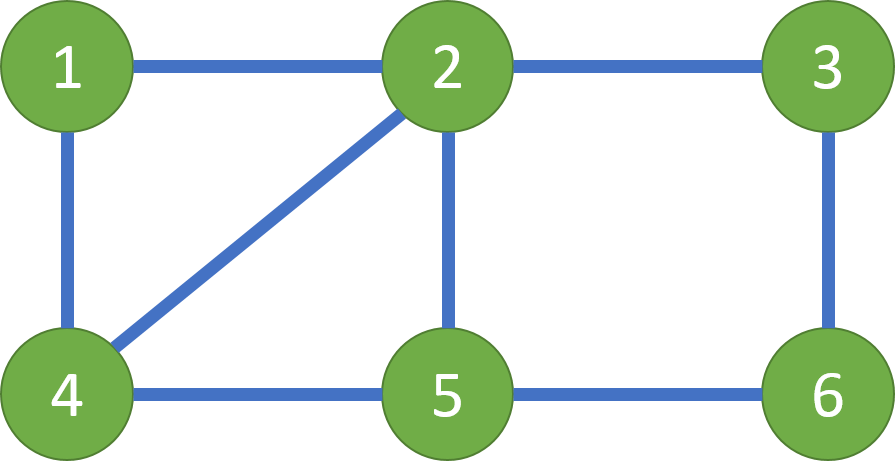
对于这个图来说，编号为4，5的点度数为奇数，其他为偶数。根据上面的性质，我们知道起点和终点一定是4、5节点。我们先从4开始随便画一条边直到无路可走：



在这一步中我们连接了4-5-6-3-2-5。根据欧拉路的构造，我们得到了L1。因为L1并没有走过所有的边，所以我们执行步骤3，可以发现对于4和2都是与子图G'重合的点，在子图上我们可以得到L2(2-4-1-2)：



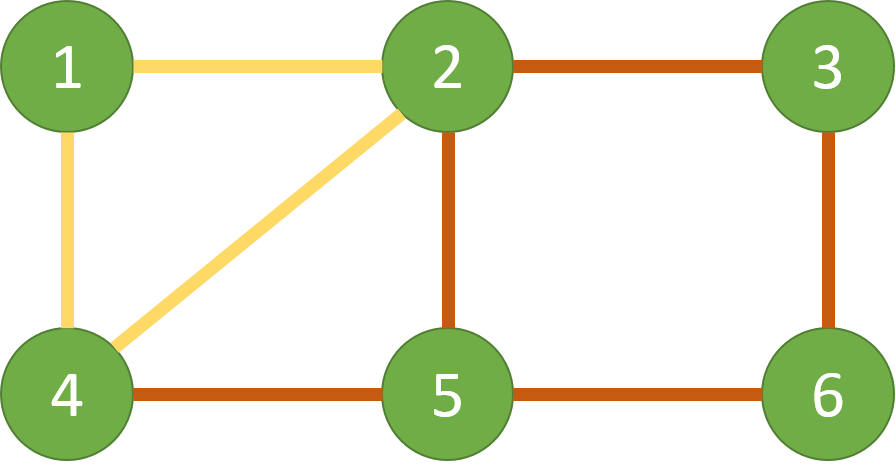
L1和L2合并就构成了欧拉路。
小Ho：既然有这个性质，那么我只需要计算每个点的度数就能知道能否走过所有的边了。
小Hi：没错，但是别忘了最重要的一点，需要整个图是连通的才行。