从多层感知器到卷积网络（一）

写在最前面

本系列文章试图以直观的思维讲解神经网络的两个种类——多层感知器(Muti-Layer Percetron)和卷积网络(Convolutional Neural Network)。这两种网络都属于前馈型网络(Feedforward network)，其中多层感知器(MLP)是最简单也是最常见的一种神经网络结构，它是所有其他神经网络结构的基础，所以不出意外，在介绍卷积网络前，不得不提一提它。卷积网络则是另外一种特殊结构的前馈网络，在图像识别方面有着惊人的效果，了解它也是百益无害。作为普通的程序员，直接看成熟的开源代码学习神经网络是一个很大挑战。Andrew Ng的Ufldl教程是一个不错的入门材料，但是课后作业用Matlab实现神经网络始终对于我们奋战在一线的程序员觉得浑身不自在，没有彻头彻尾掌握的快感。斯坦福的cs231n课程是目前我看到的最容易懂的神经网络教程，本文实现卷积网络大部分知识都是从该课程的notes上得来的，然而里面(暂时?)并没有详细介绍backprop(这是训练神经网络的一种有效的方法，后面我会提到)在卷积网络中的实现细节(这也是我卡得比较久的地方)。但是在我翻遍材料，读遍教程，看遍coursera所有神经网络相关的课程之后，最终我还是能够不借助任何现有的机器学习API(除了Numpy的矩阵向量的基本操作)，实现MLP和CNN，欣喜之余，决定总结一番，这也是本系列的来由。由于MLP是CNN的基础，文章第一篇先介绍MLP，第二篇进阶到CNN。文章尽量以浅显语言表达，对于一些生物知识也是如此，错误在所难免，希望读者指正，不胜感激。好了，有台阶可以下了，现在开始进入正题。

神经网络的由来

人是万物之灵，而大脑便是灵中灵，自从人类发现自己是通过大脑思考后，研究大脑的人便不计其数，而计算机研究者也不甘示弱，于是神经网络的计算模型便应运而生了。现在我们先回顾一下高中的生物知识，我们知道，生物神经系统的基本结构和功能单位是神经元（神经细胞），而神经元的活动和信息在神经系统中的传输则表现为一定的生物电变化及其传播。大量生物学家对大脑进行研究，并提出了神经系统工作原理的许多假设。计算机科学家估计在某天晚上读了相关的理论，然后给出了自己的理解：大体就是神经元通过树突接收到外部信号，然后对信号作出反应，要么通过轴突激发一个冲动，向回路中相邻的神经元发出信号，要么相反，不发出信号。于是计算机科学家利用这点理解，研发出了一种类似这种工作方式的模型——人工神经网络，读者可以相信，生物学家专注研究大脑那么多年的东西，岂是程序员可以简单模拟的，所以有些计算机学者为了造成不必要的误解，就刻意避开神经网络神经元这样的说法，取而代之就是简单的以“网络”（Network）“处理单位”（Unit）称呼，其实背后还隐藏着雄心壮志——人工神经网络目标并不只是简单地模仿大脑，是要变成一种超越大脑的智能。总之，我们大概是知道神经网络的由来了。

深入了解神经网络

基本结构

首先欢迎我们生物学家的神经网络登场：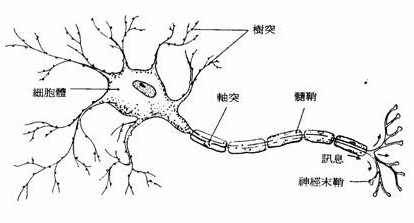



没错，这就是生物学家心目中的神经网络结构的一小部分，信号首先通过树突接收，然后经过细胞体中处理，再通过轴突传输信号给另外的神经元。 读者此时可能对计算机科学家发明的神经网络产生兴趣了，现在我们就来揭开它的庐山真面目。



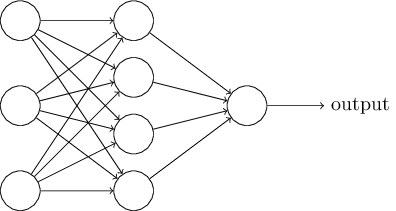
看到吧，就是这货（图是从Michael Nielsen 的书中借用的，详见http://neuralnetworksanddeeplearning.com/，该书确实很不错，图文并茂，并且有很多JS例子），图中圆圈就是大名鼎鼎的神经元，而那些带有箭头的实线可以理解为轴突和树突。这就是我们将要介绍的MLP，从左到右分别是：输入层，隐藏层，输出层。就是这样，计算机科学家认为，这样的结构可以作出图像识别，语音识别等等传统计算算法很难做出的东西。至于如何做到，读者可以先喝杯水，理清思路，听我道来。

我们不得不佩服，计算机学家实践模仿能力确实超强。首先，生物学家认为神经元会对信号进行处理，然后要么向下一个神经元传递冲动，要么抑制传递，计算机学家当然数字化一点，既然神经元会对信号处理，然后做出传递或抑制的动作，那么可以传递的时候就圆圈就输出1，抑制的时候就输出-1，太棒了，这样应该就可以模仿神经元的一部分动作了。但是这个传递过程要怎么弄呢？我们知道信号还要经过轴突的，直接将-1或1的信号作为下一个神经元的输入，就不能很好的体现这一点了。通过轴突这个通道，信号总该有所变化吧，于是模拟经过轴突的过程就是给传输信号的通道加上一些权重，就是说对于-1/1信号xx，进入下一个神经元前，必须乘上权重ww，因此下一个神经元收到的输入信号就是w∗xw*x，而不是简单的xx了。这样，很好地模拟了神经元与神经元沟通的过程，so far so good。

神经元

有了上述的总体设计之后，现在计算机科学家要进入详细设计阶段了。对于计算机而言，输入信号便是01所表达的任意数字，那么神经元接收到信号之后，如何将其输出为-1/1信号呢，一个方式就是将神经元作为一个阶跃函数，当信号w∗xw*x经过神经元时，简单对其做如下处理：

if w*x > 0:
output = 1
else:
output = -1

这种以阶跃函数模拟神经元的方式在早期被称为”感知器”(Percetron),然后多个感知器相连便是一个网络结构，然而计算机学家深入研究后，发现这种生硬地让神经元输出-1或1的方式对于以后的优化工作极其困难。那么是不是没办法了呢？我们知道凡事不要太绝对，既然直接输出-1或1对于以后的工作太困难，那么算了，我们不要那么生硬了，放宽一下限制，输出是一个-1到1的平滑范围好了，计算机学家冥思苦想，其中数学功底不错的人就联想到数学中双曲函数中的正切函数tanh不就满足这样的要求吗？！于是就有了大名鼎鼎的tanh君就登场了。tanh君对于我们理解神经网络有重大意义，现在我们稍微介绍一下他：

tanh(x)=e−x−exex+e−xtanh(x) = \frac{e^{-x}-e^{x}}{e^{x}+e^{-x}}

其导数形式为：

tanh′(x)=1−tanh2(x)tanh'(x) = 1 - tanh^2(x)

这就是tanh君的数学形象，乍看起来挺神秘的，不过不用担心，该君还是挺容易相处的，并且可以看出，其导数形式还很友好。接下来还有该君的相册，且看：



大家看到了吧，tanh君有明显的S曲线，受到广大程序员的喜爱。在x>>0x >> 0的时候输出1，在x<<0x << 0的时候，输出-1，而在其他时候便输出一个-1到1之间的数，刚好符合计算机学家的需求。所以在接下来的节目中，tanh君将会是我们的领衔主演之一。读者可能发现，既然我们用tanh模拟神经元而不是阶跃函数模拟，就不是Percetron了，那么为什么还是叫MLP呢？呵呵，回答是历史遗留问题，就像历史遗留代码，我们为了节约成本，只能忍受了。

问题提出环节

目前为止，我们已经知道计算机科学家精心发明的神经网络是如何模拟生物的神经网络系统了。然而The more we know, the more we know don’t know，仅仅知道模拟的对应过程是远远不能满足我们如黑洞般的好奇心，这里我仅代表广大群众提出几大疑惑：

具体如何获得输出呢？

怎么掌控我们的神经网络是一个识别猪的程序而不是一个识别狗的程序呢？

模拟神经元之间传递信号的权重WW是如何炼成的？

……..（此处省去问题1万个，欢迎读者踊跃提出）

问题解答环节

网络的输出

回答第一个问题之前，请读者假设我们已经解决第三个问题了，也就是我们已经获得了神经元间的权重了(不要慌张，我们一定会得到权重的！)。 好，我们正式一点介绍网络的具体形象：



咋眼一看，信息量好大，别慌，看我慢慢将其拆解：

最左边就是我们的输入层了，算是网络的第0层，通常是一个向量x:={x1,x2,x3...xn}x:=\{x_1,x_2,x_3...x_n\}（xx是一个行向量，本文对于输入都是以行向量处理）就可以搞定

对于权重WW的记法，我们是这样处理的：对于第0层的第1个神经元与第1层第1个神经元的权重，我们记为w11,1w^{1}_{1,1}，第0层第1个神经元与第1层第2个神经元的的权重，我们记为w11,2w^{1}_{1,2}。一般的，我们将权重记为wli,jw^{l}_{i,j}， 其中ll代表层数，当前第ll层，ii为第ll层的第ii个神经元，jj为第l+1l+1层的第jj个神经元，学习过线性代数的话，我们就可以用矩阵来容纳权重了，第0层和第1层之间的权重可记为：W1W^{1}，第1层与第2层之间则记为W2W^{2}，这样依此类推。

至于一个个圈圈，不是我们的神经元大哥还能是谁呢？由tanh君掌控着，靠得住

那几个格格不入的圈圈，里面只有一个＋1，是我们的bias神经元（别着急，后面会提到）

现在可以来说说神经网络如何计算输出了，我们先聚焦下图：



上图说明了网络中两个特定神经元的计算过程。如果你重新回顾一下线性代数的基础知识，你会发现有如下结论：

对于一个输入向量xx(这里xx是一个行向量)，第0层与第1层的权重矩阵为W1W^{1}，在输入第1层之前，我们知道信号将经过“轴突”这样的通道进行转换，变成一个加权分数：

s1=(W1)T∗x0+b0s^{1} = (W^{1})^{T}*x^{0} + b^0

上式中b0b^0就是所谓的bias项，为什么要添加此项呢？读者可以想象，对于普通的直线方程，如果没有bias项，直线就只能是通过原点的直线，那样的直线方程代表不了平面上所有直线，表达能力会大大下降，同样的，神经网络每一层向下一层输入也是一组线性组合:WT∗xW^T*x，这样一类比，这样的组合肯定没有WT∗x+bW^T*x+b强，所以，为了让我们的神经网络表达能力更强，每一层都会加上一个bias项。有些描述神经网络的书籍中，会使用一个小trick，就是将bias项一并融合到WW中，也就是W′={bias,w1,w2,w3,....wn}W' = \{bias,w_1,w_2,w_3,....w_n\} ，注意W′W' 中每一个元素都是一个行向量，原谅我的偷懒行为。而将1这个常数加到输入中，也就是x′={1,x1,x2,x3,...xn}x' = \{1,x_1,x_2,x_3,...x_n\}，注意x′x'中每个元素都是标量，不要混淆了哦。如果使用这样的trick，我们可以用更简洁的方式表达第0层到第1层的加权分数：

s1=(W1)′T∗x′0s^{1}= (W^{1})'^T*x'^0

算出加权分数后，接下来将交给tanh君处理了：

x1=tanh(s1)x^{1} = tanh(s^{1})

接下来第1层的输出将会变成第2层的输入x1x^{1} ，继续执行和上面一样的代码。经过层层处理，最后一层的输出就是我们想要的了(我们的输出依旧利用tanh做为非线性变换，一般实践上都是利用softmax产生一个输出概率分布来做多类分类)。利用python代码描述上面的执行过程：

def forward_prop(self,x,weights,biases):
a = x
for w,b in zip(weights,biases):
a = vec_tanh(a.dot(w) + b)
return a

好了算是解决第一问了，深呼一口气。

网络的惩罚者

在解决了第一问之后，我们马不停蹄地进入第二问。也就是如何控制网络的意图。回忆一下我们自己的学习经历，上课的时候，我们有课本可以学习，老师会提问题，如果我们答错了，老师就会叫我们回去抄十遍。那么在网络中，担任老师这个惩罚人的角色就是cost大哥（也有loss的说法）了。为了能够介绍好cost大哥，我们有必要提出一下神经网络解决的一种问题：

一般来说，神经网络解决的是监督式（supervised）问题，而监督式问题典型的情景就是，你是老师，你有大量的现成知识和例子（x，y）（x，y），对于判别猪的程序，xx可能就是（身高，体重，脚的数量）之类的特征，而yy就是简单的1或-1，1代表猪，-1代表非猪。好了，你期待当你把你所学全部传授给它的时候，对于一个以前你从未提起过的一组特征，你的学生神经网络做出正确的答案。也就是当你用一个新样本测试你的学生时，你希望你学生的回答f(x)f(x)（发挥我们的抽象思维，整个神经网络其实就是一个函数f(x)f(x)，给定一个输入xx,它会输出f(x)f(x)）和你的所拥有的答案yy是一致的。

然而，学生是调皮的，给课本(训练数据)也不会自主学习的(神经网络恰好属于这种学生)。如何培养好学生呢，且看cost大哥如何惩罚人的。

cost大哥其实形态有好多个，其中最为常见的就是square error(其他还有cross entropy等等)，在训练神经网络阶段，我们通常会在神经网络输出层接上一个cost函数，此处我们用的是square error,对于一个训练样本(x,y)而言:

cost(x,y)=(f(x)−y)2cost(x,y) = (f(x) - y) ^2

cost大哥的存在为的就是衡量神经网络的输出好坏，我们可以想象，衡量好坏最简单的做法就是比较输出f(x)f(x)与我们期待值yy输出相差多少，相差越大我们惩罚就大，大家稍微看一下，square error刚好能满足这种需求。然后呢，惩罚这种东西，对于神经网络而言，当然是越小越好了，所以网络会通过某种机制（不要急，下面就揭晓谜题）使得cost变小，也就是尽量使输出接近期待值。这样从本质上已经为我们的神经网络指明了前进的道路。有了指导思想，前进道路不再迷茫了。

回答第三个问题，同时也就回答了第二问时所说的某种机制。如何获得合适的传递信号间的权重W呢，建议读者上一下厕所，喝点水或者coffee放松一下，接下来我会另开一个小标题来说明。

网络的知识——权重

首先明确一个问题，我们为何要计算权重？

答：因为在神经网络最后一层cost大哥掌管生杀大权，我们必须尽量少地受到惩罚，而我们纵观我们的神经网络模型，未知参数也就只有边的权重，如果将神经网络表达成一个函数，那么应该长这样：

output=f(x;W)output = f(x;W)

其中WW为权重参数。而cost的square error形式就是：

cost=||f(x;W)−y||2cost = ||f(x;W) - y||^2

我们目的就是最小化cost，也就是我们的最优化问题形式为：

argminW||f(x;W)−y||2argmin_W ||f(x;W)-y||^2

其中(x,y)(x,y)就是我们已知的训练样本，只有未知参数WW。这是一个无条件的最优化问题，只要我们求出使cost最小的WW，我们就达到控制神经网络执行某种特定任务的目的。同时我们也得到了我们一直百思不得其解的WW。

如何求解该最佳化问题

答：在最优化研究中，有一个很有名的算法，就是gradient descent，亦称“梯度下降法”，想象我们的最优化的问题空间是一个连绵凹凸起伏的山脉，我们扔一个球在任意位置，然后让球沿着最陡峭的方向慢慢滚到谷底，这就是该算法的物理意义。而由该算法延伸而来有一种算法称为：stochastic gradient descent,实践中该算法（mini-batch版）可以很好解决神经网络的最优化问题。这里我们就不详细讨论该算法了，只是把大概的轮廓展现给大家：

一，计算WW的梯度ΔW\Delta W

二，选取一个学习率η\eta

三，更新W=W−η∗ΔWW = W - \eta * \Delta W

请大家对最优化研究者抱有信心，人家研究了好久，才想出的这个最优化方法。有兴趣的同学可以自己再找找这方面优化知识。太好了，我们已经有办法解决这样的最优化问题，离成功不远了。然而还有一个很重要的问题，那就是如何求取梯度ΔW\Delta W。

如何求取梯度ΔW\Delta W?

方法一

如果大家对微积分的定义还没忘记，我们可以知道对于一个可导函数g(x)g(x)，在x点上的导数定义为：

g′(x)=limh−>0g(x+h)−g(x−h)2hg'(x) = lim_{h->0} \frac{g(x+h)-g(x-h)}{2h}

那么，如果我们令hh很小很小，比如1e−51e-5,那么我们可以近似求出在xx上的导数，在我们的神经网络中，当我们选取好一个样本(xx,yy)之后，我们的最优化问题变成是：

argminW||f(x;W)−y||2argmin_W ||f(x;W)-y||^2

此时只有未知变量WW，那么我们可以将cost=||f(x;W)−y||2cost=||f(x;W)-y||^2看成是一个关于WW的函数cost(W;x,y)cost(W;x,y)其中x,yx,y为已知样本。所以，求取WW中某一个权重wli,jw_{i,j}^l的导数，我们可以如下操作：

Δwli,j=cost(wli,j+h)−cost(wli,j−h)2h\Delta w_{i,j}^l = \frac{cost(w_{i,j}^l+h)-cost(w_{i,j}^l-h)}{2h}

通过逐个改变wli,jw_{i,j}^l求取每一个wli,jw_{i,j}^l的导数，我们最终可以得到ΔW\Delta W。具体可以用python代码如下实现：

/**
* nn是我们的神经网络
* weights是我们整个网络的权重，我们将其变成一个长向量
* shapes是网络中每层权重的形状
* x,y是我们的样本
**/
def compute_num_grads(nn,x,y,shapes,weights):
e = 1e-4
perturb = np.zeros(weights.shape)
num_grad = np.zeros(weights.shape)
for i in range(len(weights)):
perturb[i] = e
w1,b1 = reconstruct(weights + perturb, shapes)
w2,b2 = reconstruct(weights - perturb, shapes)
perturb[i] = 0
loss1 = nn.cal_loss(x,y,w1,b1)
loss2= nn.cal_loss(x,y,w2,b2)
num_grad[i] = (loss1 - loss2) / (2 * e)
return num_grad

这样的方法实现起来简单，也不容易出错，但是很不幸，它具有一个致命缺点，运行太 慢！对于每一个ww，我们都必须计算两次cost，对于大型网络，拥有几百万个权重，这样的算法基本不能运行。然而因为它的实现简单不容易出错，我们通常用这种方法来检验我们接下来提到的算法的正确性，这样的检验方法称为gradient check。

方法二

接下来就轮到我们大名鼎鼎的BackPropagation算法登场了。算法基本想法是通过求解输出层cost计算得出error惩罚数，向后用公式解求出各个ww的梯度。接下来将要涉及一些微积分的运算，读者可以喝喝茶，放松放松，我们好戏开始上演了。

我们知道，微积分中有一个定律，叫做链式定律（chain rule），微积分的发明人之一是牛顿，我们知道此人背景是物理学家，那么我们当然从物理意义上理解chain rule 就不会有太大障碍：

假设在时刻tt，小球速度是vv，由速度公式可以知道 v=atv = at，而此时走过瞬时位移为ss ，我们知道，s=vts = vt。那么，我们可以验证：

∂s/∂t=∂s/∂v∗∂v/∂t\partial s/\partial t = \partial s / \partial v * \partial v / \partial t

也就是 v=∂s/∂t=∂s/∂v∗∂v/∂t=t∗a=vv = \partial s/\partial t = \partial s / \partial v * \partial v / \partial t = t*a = v

虽然这个例子很蠢，但是我们至少可以验证chain rule了。也就是说，当我们求解一个函数的导数时，可以将其分解为先求其与中间函数的导数再乘以中间函数与求解点的导数。好了，脑补一下微积分的至少后，我们可以正式推导BP算法了，大家站稳扶好了。

首先，我们观察到，对于最后一层的权重，可以公式求解出其梯度(假设最后的输出会经过一次tanh变化，使得输出处于-1到1之间)：

∂cost(sLj,yLj)∂wLij=∂||tanh(sLj)−yj||2∂wLij=0.5∗(tanh(sLj)−yLj)∗tanh′(sLj)∗xL−1i
\frac{\partial cost(s_j^L,y_j^L)} { \partial w_{ij}^L }\\= \frac{\partial ||tanh(s_j^L)-y_j||^2} {\partial w_{ij}^L} \\=0.5 * (tanh(s_j^L)-y_j^L) * tanh'(s_j^L)*x_i^{L-1}

(这里我们记最后一层为：LL )

最后一层的梯度可以利用直接求导分析得出，那么倒数第二层的权重呢，倒数第三层呢，他们的权重导数又该怎么求解呢？能不能也可以以这种公式解的方式推导呢？答案是肯定的。我们知道，神经网络的内部运行过程是：对于输入xx首先进行加权求和得到权重分数s=WT∗x+bs=W^T*x+b，然后进入神经元处理得到x=tanh(s)x = tanh(s),再将其作为输出，作为下一层神经元的输入。由以上分析，我们可以知道，对于任意wli,jw_{i,j}^l的梯度，利用chain rule可以得出：

∂cost∂wli,j=∂cost∂slj∗∂slj∂wli,j=∂cost∂slj∗x(l−1)i\frac{\partial cost}{\partial w_{i,j}^l}\\=\frac{\partial cost} { \partial s_j^l } *\frac{\partial s_j^l}{\partial w_{i,j}^l} \\=\frac{\partial cost} { \partial s_j^l } * x_i^{(l-1)}

那么现在问题就是如何求得∂cost∂slj\frac{\partial cost} { \partial s_j^l } 了，我们暂且没什么直接办法，所以不妨将其记为：

δlj=∂cost∂slj\delta_j^l = \frac{\partial cost} { \partial s_j^l }

接下来我们深入分析网络内部，请看下图(图中en正是cost)：



再次利用chain rule，我们可以得到：

∂cost∂slj=∑k∂cost∂sl+1k∗∂sl+1k∂xlj∗∂xlj∂sll=∑k∂cost∂sl+1k∗wl+1jk∗tanh′(slj)\frac{\partial cost} { \partial s_j^l }\\=\sum_k\frac{\partial cost} { \partial s_k^{l+1} } *\frac{\partial s_k^{l+1}}{\partial x_j^l} *\frac{\partial x_j^l}{\partial s_l^l}\\=\sum_k\frac{\partial cost} { \partial s_k^{l+1}} * w_{jk}^{l+1} * tanh'(s_j^l)

对比我们之前的定义：δlj=∂cost∂slj\delta_j^l = \frac{\partial cost} { \partial s_j^l }

可以得出：

δlj=∑kδl+1k∗wl+1jk∗tanh′(slj)\delta_j^l =\sum_k\delta_k^{l+1} * w_{jk}^{l+1} * tanh'(s_j^l)

我们从图上来看看这种后向传播过程：



我在forward的阶段，是认准射向神经元的链接，并向前传播，在backward阶段，我们是认准神经元发出的链接，然后向后传播。

由于最后一层δLj=(tanh(sLj)−yLj)∗tanh′(sLj)\delta_j^L = (tanh(s_j^L)-y_j^L) * tanh'(s_j^L)可以直接求出，因此我们可以通过上述方程求得任意δlj\delta_j^l，从而求得任意Δwli,j\Delta w_{i,j}^l，可以愉快地进行梯度下降优化了。具体算法框架如下：

for t = 0,1,2,3,4…….

随机取得样本(x,y)

前向计算网络每个节点的分数s

求取最后一层的δL\delta^L

利用δlj=∑kδl+1k∗wl+1jk∗tanh′(slj)\delta_j^l =\sum_k\delta_k^{l+1} * w_{jk}^{l+1} * tanh'(s_j^l)求得任意δlj\delta_j^l,并求得任意Δwli,j\Delta w_{i,j}^l

更新wli,j=wli,j−η∗Δwli,jw_{i,j}^l = w_{i,j}^l - \eta * \Delta w_{i,j}^l

对于训练集比较小的，比如1千个左右的训练集，通常t来个10万8万就可以达到很好的效果。

利用Python实现上述：

def SGD_train(self,training_data,T,eta,lamb):
for t in range(T):
x, y = rand_pick(training_data)  # that is why it called stochastic
## all the dirty work get done here
weight_grads,bias_grads = self.calculate_analytic_grads(x,y)
## finally update all the weights
self.update_weights(weight_grads,bias_grads,eta,lamb,1,n)

def calculate_analytic_grads(self, x, y):
x.shape = (1,x.shape[0])
activations, scores = self.compute_activations_scores(x)
## backward pass, compute the delta of each neuron
## after the deltas are computed,use them to compute
## the gradient of each weight
deltas = self.back_propagation(scores, y)
## grad = delta * a , remember?
w_grads,b_grads = self.compute_gradient(activations, deltas)
return w_grads,b_grads

完整代码猛戳：

http://code.taobao.org/p/NTU-HW/src/bpnn/BPNetwork.py

http://code.taobao.org/p/easy-cnn/src/FeedforwardNetwork.py

我以两种方式实现了前馈神经网络，其中第一种是完成林轩田老师的课程机器学习技法中的一个作业，只是纯粹实现前馈网络，并且里面有我学习python的多线程还有尝试其他cost函数还有其他优化方法的一些轨迹，代码长得比较难看一点。第二种是利用面向对象机制，将网络每一层抽象为一个类，代码会稍微好看一点，但是第一种更适合初学者。至此，我介绍完MLP，对于MLP，其中最难理解的部分是backprop算法，初学者大概都需要被坑几次才能彻底理解吧，好了，拥有MLP的基础，我们向CNN出发吧！

引用

Standford cs231n：http://vision.stanford.edu/teaching/cs231n/

NTU 机器学习技法：https://www.coursera.org/course/ntumltwo

neural network and deep learning：http://neuralnetworksanddeeplearning.com

百度生物神经系统图片