Splay树 学习笔记一

转载自 http://www.cnblogs.com/kuangbin/archive/2012/10/07/2714068.html
作者:Dong | 可以转载, 但必须以超链接形式标明文章原始出处和作者信息及版权声明

网址:http://dongxicheng.org/structure/splay-tree/

1、 概述

二叉查找树（Binary Search Tree，也叫二叉排序树，即Binary Sort Tree）能够支持多种动态集合操作，它可以用来表示有序集合、建立索引等，因而在实际应用中，二叉排序树是一种非常重要的数据结构。

从算法复杂度角度考虑，我们知道，作用于二叉查找树上的基本操作（如查找，插入等）的时间复杂度与树的高度成正比。对一个含n个节点的完全二叉树，这些操作的最坏情况运行时间为O(log n)。但如果因为频繁的删除和插入操作，导致树退化成一个n个节点的线性链（此时即为一个单链表），则这些操作的最坏情况运行时间为O(n)。为了克服以上缺点，很多二叉查找树的变形出现了，如红黑树、AVL树，Treap树等。

本文介绍了二叉查找树的一种改进数据结构–伸展树（Splay Tree）。它的主要特点是不会保证树一直是平衡的，但各种操作的平摊时间复杂度是O(log n)，因而，从平摊复杂度上看，二叉查找树也是一种平衡二叉树。另外，相比于其他树状数据结构（如红黑树，AVL树等），伸展树的空间要求与编程复杂度要小得多。

2、 基本操作

伸展树的出发点是这样的：考虑到局部性原理（刚被访问的内容下次可能仍会被访问，查找次数多的内容可能下一次会被访问），为了使整个查找时间更小，被查频率高的那些节点应当经常处于靠近树根的位置。这样，很容易得想到以下这个方案：每次查找节点之后对树进行重构，把被查找的节点搬移到树根，这种自调整形式的二叉查找树就是伸展树。每次对伸展树进行操作后，它均会通过旋转的方法把被访问节点旋转到树根的位置。

为了将当前被访问节点旋转到树根，我们通常将节点自底向上旋转，直至该节点成为树根为止。“旋转”的巧妙之处就是在不打乱数列中数据大小关系（指中序遍历结果是全序的）情况下，所有基本操作的平摊复杂度仍为O（log n）。

伸展树主要有三种旋转操作，分别为单旋转，一字形旋转和之字形旋转。为了便于解释，我们假设当前被访问节点为X，X的父亲节点为Y（如果X的父亲节点存在），X的祖父节点为Z（如果X的祖父节点存在）。

（1） 单旋转

节点X的父节点Y是根节点。这时，如果X是Y的左孩子，我们进行一次右旋操作；如果X 是Y 的右孩子，则我们进行一次左旋操作。经过旋转，X成为二叉查找树T的根节点，调整结束。



（2） 一字型旋转

节点X 的父节点Y不是根节点，Y 的父节点为Z，且X与Y同时是各自父节点的左孩子或者同时是各自父节点的右孩子。这时，我们进行一次左左旋转操作或者右右旋转操作。



（3） 之字形旋转

节点X的父节点Y不是根节点，Y的父节点为Z，X与Y中一个是其父节点的左孩子而另一个是其父节点的右孩子。这时，我们进行一次左右旋转操作或者右左旋转操作。



3、伸展树区间操作

在实际应用中，伸展树的中序遍历即为我们维护的数列，这就引出一个问题，怎么在伸展树中表示某个区间？比如我们要提取区间[a,b]，那么我们将a前面一个数对应的结点转到树根，将b 后面一个结点对应的结点转到树根的右边，那么根右边的左子树就对应了区间[a,b]。原因很简单，将a 前面一个数对应的结点转到树根后， a 及a 后面的数就在根的右子树上，然后又将b后面一个结点对应的结点转到树根的右边，那么[a,b]这个区间就是下图中B所示的子树。



利用区间操作我们可以实现线段树的一些功能，比如回答对区间的询问（最大值，最小值等）。具体可以这样实现，在每个结点记录关于以这个结点为根的子树的信息，然后询问时先提取区间，再直接读取子树的相关信息。还可以对区间进行整体修改，这也要用到与线段树类似的延迟标记技术，即对于每个结点，额外记录一个或多个标记，表示以这个结点为根的子树是否被进行了某种操作，并且这种操作影响其子结点的信息值，当进行旋转和其他一些操作时相应地将标记向下传递。

与线段树相比，伸展树功能更强大，它能解决以下两个线段树不能解决的问题：

（1） 在a后面插入一些数。方法是：首先利用要插入的数构造一棵伸展树，接着，将a 转到根，并将a 后面一个数对应的结点转到根结点的右边，最后将这棵新的子树挂到根右子结点的左子结点上。

（2） 删除区间[a,b]内的数。首先提取[a,b]区间，直接删除即可。

4、实现

代码全部来自【参考资料2】。

（1）旋转操作

（2）splay操作

（3）将第k个数转到要求的位置

5、 应用

（1） 数列维护问题

题目：维护一个数列，支持以下几种操作：

1. 插入：在当前数列第posi 个数字后面插入tot 个数字；若在数列首位插入，则posi 为0。

2. 删除：从当前数列第posi 个数字开始连续删除tot 个数字。

3. 修改：从当前数列第posi 个数字开始连续tot 个数字统一修改为c 。

4. 翻转：取出从当前数列第posi 个数字开始的tot 个数字，翻转后放入原来的位置。

5. 求和：计算从当前数列第posi 个数字开始连续tot 个数字的和并输出。

6. 求和最大子序列：求出当前数列中和最大的一段子序列，并输出最大和。

（2） 轻量级web服务器lighttpd中用到数据结构splay tree.

6、 参考资料

（1） 杨思雨《伸展树的基本操作与应用》

（2） Crash《运用伸展树解决数列维护问题》

MiYu原创, 转帖请注明 : 转载自 ______________白白の屋


伸展树(Splay Tree)是AVL树不错的替代，它有以下几个特点：

(1)它是二叉查找树的改进，所以具有二叉查找树的有序性。

(2)对伸展树的操作的平摊复杂度是O(log2n)。

(3)伸展树的空间要求、编程难度非常低。

提到伸展树，就不得不提到AVL树和Read-Black树，虽然这两种树能够保证各种操作在最坏情况下都为logN，但是两都实现都比较复杂。而在实际情况中，90%的访问发生在10%的数据上。因此，我们可以重构树的结构，使得被经常访问的节点朝树根的方向移动。尽管这会引入额外的操作，但是经常被访问的节点被移动到了靠近根的位置，因此，对于这部分节点，我们可以很快的访问。这样，就能使得平摊复杂度为logN。

1、自底向上的伸展树

伸展操作Splay(x,S)是在保持伸展树有序性的前提下，通过一系列旋转操作将伸展树S中的元素x调整至树的根部的操作。

在旋转的过程中，要分三种情况分别处理：

(1)Zig 或 Zag

(2)Zig-Zig 或 Zag-Zag

(3)Zig-Zag 或 Zag-Zig

1.1、Zig或Zag操作

节点x的父节点y是根节点。



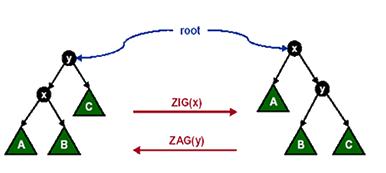
1.2、Zig-Zig或Zag-Zag操作

节点x的父节点y不是根节点，且x与y同时是各自父节点的左孩子或者同时是各自父节点的右孩子。



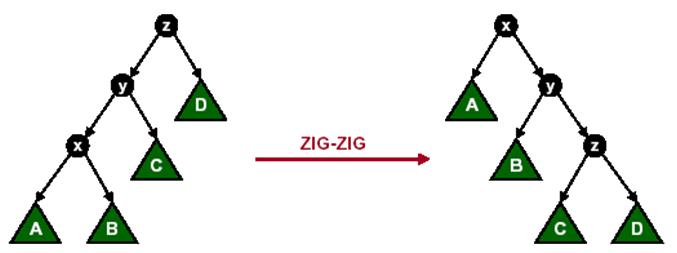
1.3、Zig-Zag或Zag-Zig操作

节点x的父节点y不是根节点，x与y中一个是其父节点的左孩子而另一个是其父节点的右孩子。



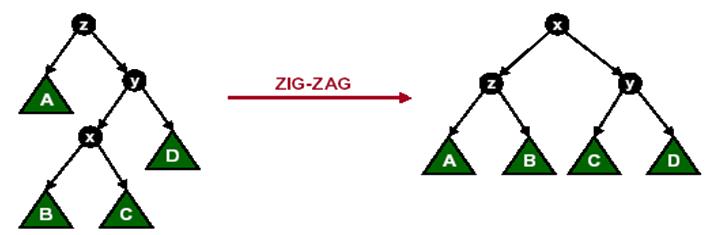
2、自顶向下的伸展树

在自底向上的伸展树中，我们需要求一个节点的父节点和祖父节点，因此这种伸展树难以实现。因此，我们可以构建自顶向下的伸展树。

当我们沿着树向下搜索某个节点X的时候，我们将搜索路径上的节点及其子树移走。我们构建两棵临时的树──左树和右树。没有被移走的节点构成的树称作中树。在伸展操作的过程中：

(1)当前节点X是中树的根。

(2)左树L保存小于X的节点。

(3)右树R保存大于X的节点。

开始时候，X是树T的根，左右树L和R都是空的。和前面的自下而上相同，自上而下也分三种情况：

2.1、Zig操作



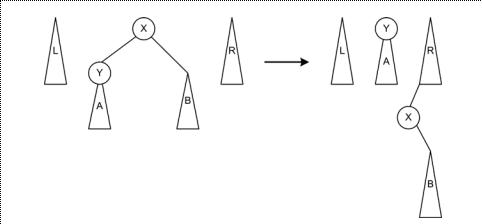
如上图，在搜索到X的时候，所查找的节点比X小，将Y旋转到中树的树根。旋转之后，X及其右子树被移动到右树上。很显然，右树上的节点都大于所要查找的节点。注意X被放置在右树的最小的位置，也就是X及其子树比原先的右树中所有的节点都要小。这是由于越是在路径前面被移动到右树的节点，其值越大。

2.2、Zig-Zig操作



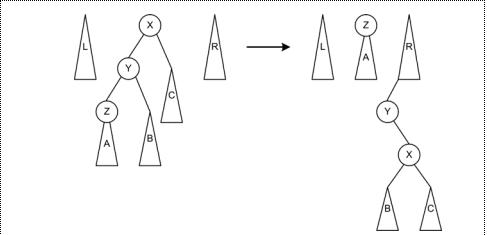
这种情况下，所查找的节点在Z的子树中，也就是，所查找的节点比X和Y都小。所以要将X，Y及其右子树都移动到右树中。首先是Y绕X右旋，然后Z绕Y右旋，最后将Z的右子树（此时Z的右子节点为Y）移动到右树中。

2.3、Zig-Zag操作



这种情况中，首先将Y右旋到根。这和Zig的情况是一样的，然后变成上图右边所示的形状。此时，就与Zag(与Zig相反)的情况一样了。

最后，在查找到节点后，将三棵树合并。如图：



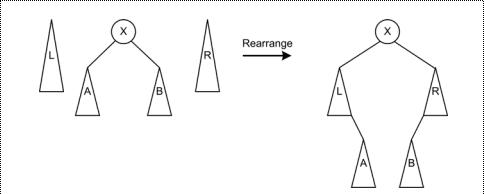
2.4、示例：

下面是一个查找节点19的例子。在例子中，树中并没有节点19,最后，距离节点最近的节点18被旋转到了根作为新的根。节点20也是距离节点19最近的节点，但是节点20没有成为新根，这和节点20在原来树中的位置有关系。



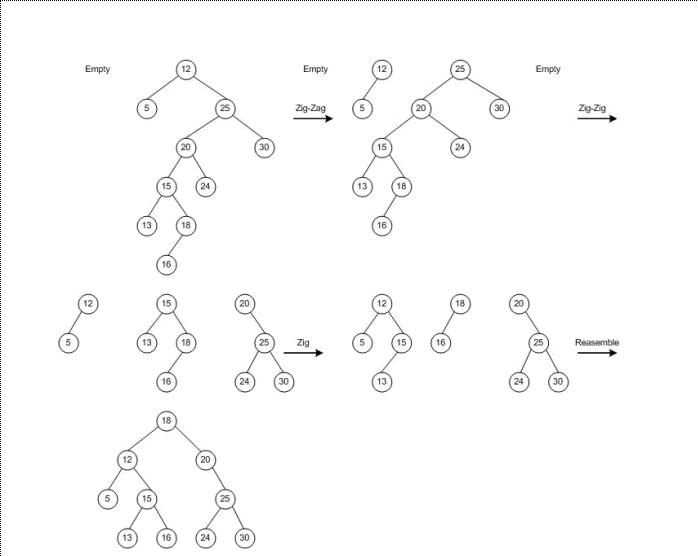
3、实现

3.1、splay操作


代码
tree_node * splay (int i, tree_node * t) {

tree_node N, *l, *r, *y;

if (t == NULL)

return t;

N.left = N.right = NULL;

l = r = &N;

for (;;)

{

if (i < t->item)

{

if (t->left == NULL)

break;

if (i < t->left->item)

{

y = t->left; /* rotate right */

t->left = y->right;

y->right = t;

t = y;

if (t->left == NULL)

break;

}

r->left = t; /* link right */

r = t;

t = t->left;

} else if (i > t->item)

{

if (t->right == NULL)

break;

if (i > t->right->item)

{

y = t->right; /* rotate left */

t->right = y->left;

y->left = t;

t = y;

if (t->right == NULL)

break;

}

l->right = t; /* link left */

l = t;

t = t->right;

} else {

break;

}

}

l->right = t->left; /* assemble */

r->left = t->right;

t->left = N.right;

t->right = N.left;

return t;

}

Rotate right(查找10)：



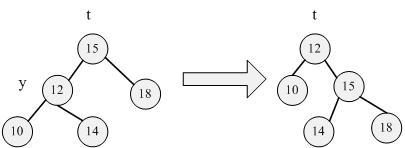
Link right：



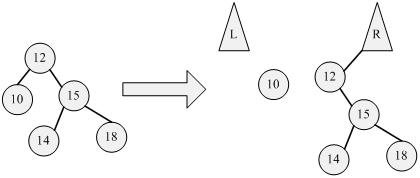
Assemble：



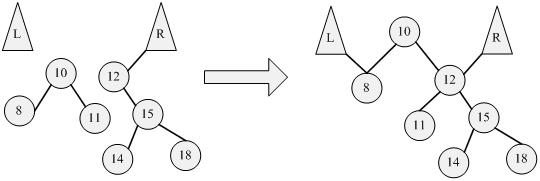
Rotate left(查找20)：



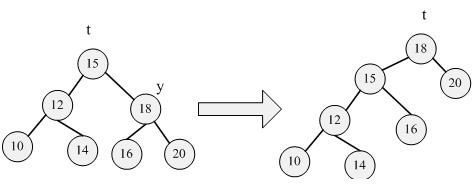
Link left：



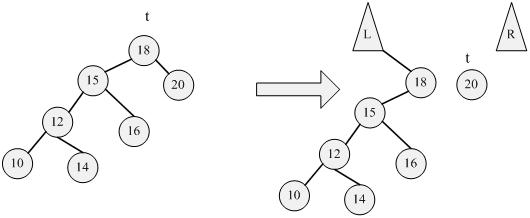
3.2、插入操作


代码
/*

**将i插入树t中,返回树的根结点(item值==i)

*/

tree_node* ST_insert(int i, tree_node *t) {

/* Insert i into the tree t, unless it's already there. */

/* Return a pointer to the resulting tree. */

tree_node* node;

node = (tree_node *) malloc (sizeof (tree_node));

if (node == NULL){

printf("Ran out of space\n");

exit(1);

}

node->item = i;

if (t == NULL) {

node->left = node->right = NULL;

size = 1;

return node;

}

t = splay(i,t);

if (i < t->item) { //令t为i的右子树

node->left = t->left;

node->right = t;

t->left = NULL;

size ++;

return node;

} else if (i > t->item) { //令t为i的左子树

node->right = t->right;

node->left = t;

t->right = NULL;

size++;

return node;

} else {

free(node); //i值已经存在于树t中

return t;

}

}

3.3、删除操作

代码
/*

**从树中删除i,返回树的根结点

*/

tree_node* ST_delete(int i, tree_node* t) {

/* Deletes i from the tree if it's there. */

/* Return a pointer to the resulting tree. */

tree_node* x;

if (t==NULL)

return NULL;

t = splay(i,t);

if (i == t->item) { /* found it */

if (t->left == NULL) { //左子树为空,则x指向右子树即可

x = t->right;

} else {

x = splay(i, t->left); //查找左子树中最大结点max,令右子树为max的右子树

x->right = t->right;

}

size--;

free(t);

return x;

}

return t; /* It wasn't there */

}

完整代码：


代码
#include <stdio.h>

#include <stdlib.h>

int size; //结点数量

#define NUM 20

typedef struct tree_node{

struct tree_node* left;

struct tree_node* right;

int item;

}tree_node;

tree_node* splay (int i, tree_node* t) {

tree_node N, *l, *r, *y;

if (t == NULL)

return t;

N.left = N.right = NULL;

l = r = &N;

for (;;)

{

if (i < t->item)

{

if (t->left == NULL)

break;

if (i < t->left->item)

{

y = t->left; /* rotate right */

t->left = y->right;

y->right = t;

t = y;

if (t->left == NULL)

break;

}

r->left = t; /* link right */

r = t;

t = t->left;

} else if (i > t->item)

{

if (t->right == NULL)

break;

if (i > t->right->item)

{

y = t->right; /* rotate left */

t->right = y->left;

y->left = t;

t = y;

if (t->right == NULL)

break;

}

l->right = t; /* link left */

l = t;

t = t->right;

} else {

break;

}

}

l->right = t->left; /* assemble */

r->left = t->right;

t->left = N.right;

t->right = N.left;

return t;

}

/*

**将i插入树t中,返回树的根结点(item值==i)

*/

tree_node* ST_insert(int i, tree_node *t) {

/* Insert i into the tree t, unless it's already there. */

/* Return a pointer to the resulting tree. */

tree_node* node;

node = (tree_node *) malloc (sizeof (tree_node));

if (node == NULL){

printf("Ran out of space\n");

exit(1);

}

node->item = i;

if (t == NULL) {

node->left = node->right = NULL;

size = 1;

return node;

}

t = splay(i,t);

if (i < t->item) { //令t为i的右子树

node->left = t->left;

node->right = t;

t->left = NULL;

size ++;

return node;

} else if (i > t->item) { //令t为i的左子树

node->right = t->right;

node->left = t;

t->right = NULL;

size++;

return node;

} else {

free(node); //i值已经存在于树t中

return t;

}

}

/*

**从树中删除i,返回树的根结点

*/

tree_node* ST_delete(int i, tree_node* t) {

/* Deletes i from the tree if it's there. */

/* Return a pointer to the resulting tree. */

tree_node* x;

if (t==NULL)

return NULL;

t = splay(i,t);

if (i == t->item) { /* found it */

if (t->left == NULL) { //左子树为空,则x指向右子树即可

x = t->right;

} else {

x = splay(i, t->left); //查找左子树中最大结点max,令右子树为max的右子树

x->right = t->right;

}

size--;

free(t);

return x;

}

return t; /* It wasn't there */

}

void ST_inoder_traverse(tree_node* node)

{

if(node != NULL)

{

ST_inoder_traverse(node->left);

printf("%d ", node->item);

ST_inoder_traverse(node->right);

}

}

void ST_pre_traverse(tree_node* node)

{

if(node != NULL)

{

printf("%d ", node->item);

ST_pre_traverse(node->left);

ST_pre_traverse(node->right);

}

}

void main() {

/* A sample use of these functions. Start with the empty tree, */

/* insert some stuff into it, and then delete it */

tree_node* root;

int i;

root = NULL; /* the empty tree */

size = 0;

for(i = 0; i < NUM; i++)

root = ST_insert(rand()%NUM, root);

ST_pre_traverse(root);

printf("\n");

ST_inoder_traverse(root);

for(i = 0; i < NUM; i++)

root = ST_delete(i, root);

printf("\nsize = %d\n", size);

}