傅里叶与离散余弦（计算机图像处理实现）研究

前言

自我感悟，学习的最高境界不在于将知识融会贯通，而在于能将知识浅显易懂的讲述和传授于爱好学习的人。自己能将知识学习的扎实，那还只是自己一人的成就，而当将知识通过清晰的语言,形象的图形,规整的表格来讲述给他人时，那是你我他之间大家的成就。

理论基础

什么是图像变换？

为了不仅仅从时间和空间的角度来分析一张图片和实现数字图像压缩，为了达到对图像处理后HVS（这个好高级的英文概念，其实指的是你自己的双眼）几乎发现不了任何差别，从人类视觉最敏感的图像区域处理的方案是不行的，伟大的数学家们，研究出可以从别的区域（比如频域）来实现压缩图像信息而达到人眼不能觉察图像已经受过处理，所以对图像进行处理，即图像变换。

什么是正交空间？

一说到正交空间，就不说的它的概念了，说了也不记得。它的作用其实就如同初中时，学函数基本概念的坐标轴x轴和y轴，正如同时空域分析离散余弦变换的时域和空域。sin(nx)和cos(nx)就正如x轴和y轴。

什么是离散余弦变换和傅里叶变换？

通过一张图可以看出为什么在FT和DCT中，f(x)为什么需要乘一个三角函数来得到频域函数（FT中的复指数其实就是两个正弦函数，而DCT中由于它的第二个正弦函数表示为0值，所以形式如同an*cos(nx))。

任何连续周期信号都可以由一组适当的正余弦曲线组合而成，意思就是指f(x)可以由一些正余弦函数四则运算表示。

二维DCT算法的实现

1.通过二维DCT转换成一维DCT来实现二维DCT算法。

一维DCT公式：







算法代码实现（c语言）：

void DCT_1D(double src[8],double dst[8]){//长度N=8的一维余弦变化
double cu,tmp;
for(int u=0;u<8;u++){
tmp=0;
if(u==0){
cu=1.0/sqrt(8.0);
}
else{
cu=1.0/sqrt(4.0);
}
for(int x=0;x<8;x++){
tmp+=src[x]*cos((2*(double)x+1)*u*pi/16.0);
}
dst[u]=cu*tmp;
}
}

二维DCT公式：





算法代码实现（c语言）：

void DCT_2D(double src_block[8][8], double coefficient_block[8][8])//src为原图像矩阵，dst为DCT后的系数矩阵 8*8像素小块
{
for(int u = 0; u < 8; u++)
for(int v = 0; v < 8; v++)
{
double tmp = 0;
double cu = 1, cv = 1;
if(u == 0)
cu = 1.0 / sqrt(2.0);
if(v == 0)
cv = 1.0 / sqrt(2.0);
for(int i = 0; i < 8; i++)
for(int j = 0; j < 8; j++)
tmp += (double)src_block[i][j] * cos((2 * (double)i + 1) * (double)u * pi / 16.0) * cos((2 * (double)j + 1) * (double)v * pi / 16.0);
tmp *= 0.25 * cu * cv;
coefficient_block[u][v] = tmp >= 0 ? tmp + 0.5 : tmp - 0.5;	//四舍五入取整
}
}

2.通过一维DCT算法来进一步优化二维DCT算法

对二维分析，可以发现可以转换为一维来处理，下面这个式子z(v,i)是中间变量，x(i,j)为输入的原数据



算法代码实现（c语言）：

void DCT_2D(double src_block[8][8], double coefficient_block[8][8]){
double z[8][8];
double tmp;
double cu = 1.0, cv = 1.0;
for(int v=0;v<8;v++){
if(v == 0)
cv = 1.0 / sqrt(2.0);
else
cv=1.0;
for(int i=0;i<8;i++){
tmp=0;
for(int j=0;j<8;j++){
tmp+=(cv*src_block[i][j]*cos((2*(double)j+1.0)*(double)v*pi/16.0));
}
z[v][i]=1.0/sqrt(4.0)*tmp;
}
for(int u=0;u<8;u++){
if(u == 0)
cu = 1.0 / sqrt(2.0);
else
cu=1.0;
tmp=0;
for(int i=0;i<8;i++){
tmp=tmp+(cu*z[v][i]*cos((2*(double)i+1.0)*(double)u*pi/16.0));
}
tmp=1.0/sqrt(4.0)*tmp;
coefficient_block[u][v]= tmp >= 0 ? tmp + 0.5 : tmp - 0.5;
}
}
}

优化算法还有ChenDCT，LeeDCT，AAN 算法和 LLM 算法这些，有关这些优化的网上代码都不知道作者有木有验证算法代码的正确性，运行出来的答案与本人自己标准的一维DCT变换一点也不相同。

3.通过傅里叶变换来实现，可以在一维优化算法中再进一步利用一维傅里叶优化或者实现二维傅里叶实现二维离散余弦变换。

傅里叶的学习道路是坎坷的，最不了解是傅里叶变换的形象描述，应用自july博客的原文和上面那个GIF图来描述傅里叶变换

频谱密度就象物理中物质密度，原始信号中的每一个点就像是一个混合物，这个混合物是由不同密度的物质组成的，混合物中含有的每种物质的质量是一样的，除了最大和最小两个密度的物质外，这样我们只要把每种物质的密度加起来就可以得到该混合物的密度了，又该混合物的质量是单位质量，所以得到的密度值跟该混合物的质量值是一样的。

下面这张图清晰的表述出变换前后时间和频域的函数曲线的相关性



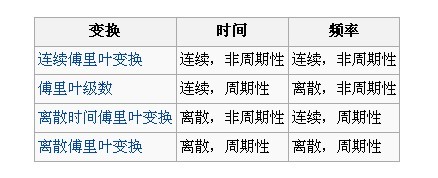
傅里叶数学公式来：





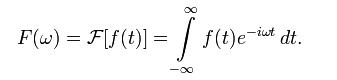
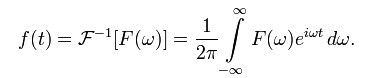
f(x)乘以的e的复指数，通过欧拉公式是可以展开为一个正弦函数和一个余弦函数，余弦的部分是实数，而正弦的部分是复数，可以通过离散余弦和离散傅里叶之间的计算相似性，来利用傅里叶优化离散余弦变换。又发一张草稿图来特别说明：

(1)一维傅里叶变换优化一维离散余弦变换

算法代码实现（c语言）：

typedef struct complex{
double x;
double y;
}complex;

void FFT_th(complex *TD,complex *FD,int r){
int count;
int i,j,k;
int bfsize,p;
double angle;
complex *W,*X1,*X2,*X;
count=1<<r;
W =new complex[count/2];
X1=new complex[count];
X2=new complex[count];
for(i=0;i<count/2;i++)
{
angle=-i*pi*2/count;
W[i].x=cos(angle);
W[i].y=sin(angle);
}
memcpy(X1,TD,sizeof(complex)*count);
for(k = 0; k < r; k++)
{
for(j = 0; j < 1 << k; j++)
{
bfsize = 1 << (r-k);
for(i = 0; i < bfsize / 2; i++)
{
p = j * bfsize;
X2[i + p].x = X1[i + p].x + X1[i + p + bfsize / 2].x;
X2[i + p].y = X1[i + p].y + X1[i + p + bfsize / 2].y;
double m_x,m_y;
m_x=(X1[i + p].x - X1[i + p + bfsize / 2].x);
m_y=(X1[i + p].y - X1[i + p + bfsize / 2].y);
X2[i + p + bfsize / 2].x =m_x*W[i*(1<<k)].x-m_y*W[i*(1<<k)].y;
X2[i + p + bfsize / 2].y =m_y*W[i*(1<<k)].x+m_x*W[i*(1<<k)].y;

}
}
X  = X1;
X1 = X2;
X2 = X;
}
for(j = 0; j < count; j++)
{
p = 0;
for(i = 0; i < r; i++)
{
if (j&(1<<i))
{
p+=1<<(r-i-1);
}
}
FD[j]=X1[p];
}
delete W;
delete X1;
delete X2;
return ;
}
void DCT_FFT(double *f, double *F, int r)
{
int count;
int  i;
double dTemp;
complex *X;
count = 1<<r;
X = new complex[count*2];
memset(X, 0, sizeof(complex)*count*2);
for(i=0;i<count;i++)
{
X[i].x =f[i];
X[i].y=0;
}
FFT_th(X,X,r+1);
dTemp = 1.0/sqrt((double)count);
F[0] = X[0].x* dTemp;
dTemp *= sqrt(2.0);
for(i = 1; i < count; i++)
{
F[i]=(X[i].x*cos(i*pi/(count*2.0))+X[i].y*sin(i*pi/(count*2.0)))*dTemp;
}
delete X;
}

void DCT64(unsigned char src_block[8][8],int res_block[8][8]){
double z[8][8];
double tmp;
double cu = 1.0, cv = 1.0;
for(int v=0;v<8;v++){
if(v == 0)
cv = 1.0 / sqrt(2.0);
else
cv=1.0;
for(int i=0;i<8;i++){
tmp=0;
//以下也可以通过一维傅里叶来优化
for(int j=0;j<8;j++){
tmp+=(cv*(double)src_block[i][j]*cos((2*(double)j+1.0)*(double)v*pi/16.0));
}
z[v][i]=1.0/sqrt(4.0)*tmp;

}
double in[8],ans[8];
for(int i=0;i<8;i++){
in[i]=z[v][i];
}</span><div><span style="font-size:14px;"></span><div><span style="font-size:14px;">
</span></div></div><span style="font-size:14px;">     DCT_FFT(in,ans,3);//一维傅里叶实现优化
for(int u=0;u<8;u++){
if(u == 0)
cu = 1.0 / sqrt(2.0);
else
cu=1.0;
tmp=ans[u];
res_block[u][v]= tmp >= 0 ? tmp + 0.5 : tmp - 0.5;
}
}
}

(2)二维离散傅里叶变换实现二维离散余弦变换

理论上是可以实现的，有时限问题，将来需要研究开发时，再将原理和代码附上。