[POJ][1003]Hangover
2013-10-04 20:41
288 查看
Description
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the
bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1)
card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.
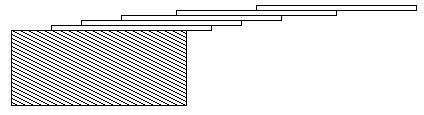
Input
The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will
contain exactly three digits.
Output
For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.
Sample Input
Sample Output
这是传说中的水题,题目说的物理原理正确与否我不知道,得出结果还是很简单的,只是简单的模拟,而且仅仅是float类型就能搞定,直接给出AC代码
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the
bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1)
card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.

Input
The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will
contain exactly three digits.
Output
For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.
Sample Input
1.00 3.71 0.04 5.19 0.00
Sample Output
3 card(s) 61 card(s) 1 card(s) 273 card(s)
这是传说中的水题,题目说的物理原理正确与否我不知道,得出结果还是很简单的,只是简单的模拟,而且仅仅是float类型就能搞定,直接给出AC代码
#include<iostream>
using namespace std;
int main()
{
float c;
cin>>c;
while(c!=0)
{
int n=1;
float num=1/float(n+1);
while(num<c) num+=1/float(++n+1);
cout<<n<<" card(s)"<<endl;
cin>>c;
}
return 0;
}
相关文章推荐
- [转][源代码]Comex公布JailbreakMe 3.0源代码
- LCL.VBS 病毒源代码
- jQuery-digest | 咀嚼jQuery源码
- [源码]Norton Ghost C# 源代码
- [源代码]symantec远程控制软件PcAnywhere源代码分享
- [源代码]Torque3D引擎SDK
- [游戏源码]Doom3公布源代码下载
- 《Doom 3》源代码将在《Rage》上市后免费发布
- 【资料分享】网游[天龙八部]源代码分享
- Android系统默认Home应用程序(Launcher)的启动过程源代码分析
- 65个源代码网站
- 一个游戏程序员的学习资料
- 剖析top命令显示的VIRT RES SHR值
- CentOS 6.3下Apache+SVN部署Web版本同步
- Python入门书籍(中文版)
- Linux下Samba源代码安装以及环境配置
- 开源硬件监控软件:Open Hardware Monitor
- Linux之父盟友分道扬镳 直言开源模式软肋
- Linux vs BSD我们到底选择谁!
- 嵌入式系统开发,不用Linux的理由 ! (转,这个有点牛!)
