Little's Law
2012-08-29 12:07
471 查看
这是排队论中最简单的一个定理,描述了平均队长、等待时间和到达率之间的关系。
L:平均队长, W:等待时间, Lambda:到达率
L = W * Lambda
理解该公式有几点需要注意:
1. 必须是稳定系统,即:“人”离开的速率必须大于或等于到达的速率,否则系统中的等待数将会越来越大,队长最终趋向于无穷大。
2. 等待时间可以理解成队列中最后一个“人”加入到队列中,直到他被服务为止的时间。
我们不妨观察队列中最后一个人,包括他在内前面一共有L个人,他最终要等待W秒才被服务,那么可以想象,这W秒后,系统中又进来了L个人。因此,系统的到达率为:Lambda = L / W
例1:
在一个网络系统中,假设我们的缓冲区可以缓冲1000个请求,每个请求的平均服务时间为0.001秒(1ms),那么这个系统中的数据包的平均等待时间为1000 * 0.001 = 1秒
Lambda = 1000 / 1 = 1000
也就是说,该系统每秒最多能够处理1000个请求。
例2:
假设我们观察到向一个系统发送请求,平均20ms就能得到响应,并且该系统每秒能处理大约1000个请求,那么是否能推测出该系统的缓冲区长度?
Lambda = 1000, W = 0.02, 所以: L = 20
实际上,为了应付瞬时尖峰请求,队长应该比20大一些(一般的经验值是多少呢?)。另外,实际系统中还会通过丢包、拒绝请求的方式控制队长。
参考:http://en.wikipedia.org/wiki/Little%27s_law#Example
Imagine a small store with a single counter and an area for browsing, where only one person can be at the counter at a time, and no one leaves without buying something. So the system is roughly:
Entrance → Browsing → Counter → Exit
This is a stable system, so the rate at which people enter the store is the rate at which they arrive at the store, and the rate at which they exit as well. We call this the arrival rate. By contrast, an arrival rate exceeding an exit rate would represent an
unstable system, where the number of waiting customers in the store will gradually increase towards infinity.
Little's Law tells us that the average number of customers in the store, L, is the effective arrival rate, λ, times the average time that a customer spends in the store, W, or simply:

Assume customers arrive at the rate of 10 per hour and stay an average of 0.5 hour. This means we should find the average number of customers in the store at any time to be 5.
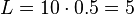
Now suppose the store is considering doing more advertising to raise the arrival rate to 20 per hour. The store must either be prepared to host an average of 10 occupants or must reduce the time each customer spends in the store to 0.25 hour. The store might
achieve the latter by ringing up the bill faster or by adding more counters.
We can apply Little's Law to systems within the store. For example, the counter and its queue. Assume we notice that there are on average 2 customers in the queue and at the counter. We know the arrival rate is 10 per hour, so customers must be spending 0.2
hours on average checking out.
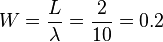
We can even apply Little's Law to the counter itself. The average number of people at the counter would be in the range (0, 1) since no more than one person can be at the counter at a time. In that case, the average number of people at the counter is also known
as the utilisation of the counter.
However, because a store in reality generally has a limited amount of space, it cannot become unstable. Even if the arrival rate is much greater than the exit rate, the store will eventually start to overflow, and thus any new arriving customers will simply
be rejected (and forced to go somewhere else or try again later) until there is once again free space available in the store. This is also the difference between the arrival rate and the effective arrival rate, where the arrival rate roughly
corresponds to the rate of which customers arrive at the store, whereas the effective arrival rate corresponds to the rate of which customers enter the store. In a system with an infinite size and no loss, the two are however equal.
L:平均队长, W:等待时间, Lambda:到达率
L = W * Lambda
理解该公式有几点需要注意:
1. 必须是稳定系统,即:“人”离开的速率必须大于或等于到达的速率,否则系统中的等待数将会越来越大,队长最终趋向于无穷大。
2. 等待时间可以理解成队列中最后一个“人”加入到队列中,直到他被服务为止的时间。
我们不妨观察队列中最后一个人,包括他在内前面一共有L个人,他最终要等待W秒才被服务,那么可以想象,这W秒后,系统中又进来了L个人。因此,系统的到达率为:Lambda = L / W
例1:
在一个网络系统中,假设我们的缓冲区可以缓冲1000个请求,每个请求的平均服务时间为0.001秒(1ms),那么这个系统中的数据包的平均等待时间为1000 * 0.001 = 1秒
Lambda = 1000 / 1 = 1000
也就是说,该系统每秒最多能够处理1000个请求。
例2:
假设我们观察到向一个系统发送请求,平均20ms就能得到响应,并且该系统每秒能处理大约1000个请求,那么是否能推测出该系统的缓冲区长度?
Lambda = 1000, W = 0.02, 所以: L = 20
实际上,为了应付瞬时尖峰请求,队长应该比20大一些(一般的经验值是多少呢?)。另外,实际系统中还会通过丢包、拒绝请求的方式控制队长。
参考:http://en.wikipedia.org/wiki/Little%27s_law#Example
Imagine a small store with a single counter and an area for browsing, where only one person can be at the counter at a time, and no one leaves without buying something. So the system is roughly:
Entrance → Browsing → Counter → Exit
This is a stable system, so the rate at which people enter the store is the rate at which they arrive at the store, and the rate at which they exit as well. We call this the arrival rate. By contrast, an arrival rate exceeding an exit rate would represent an
unstable system, where the number of waiting customers in the store will gradually increase towards infinity.
Little's Law tells us that the average number of customers in the store, L, is the effective arrival rate, λ, times the average time that a customer spends in the store, W, or simply:

Assume customers arrive at the rate of 10 per hour and stay an average of 0.5 hour. This means we should find the average number of customers in the store at any time to be 5.
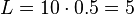
Now suppose the store is considering doing more advertising to raise the arrival rate to 20 per hour. The store must either be prepared to host an average of 10 occupants or must reduce the time each customer spends in the store to 0.25 hour. The store might
achieve the latter by ringing up the bill faster or by adding more counters.
We can apply Little's Law to systems within the store. For example, the counter and its queue. Assume we notice that there are on average 2 customers in the queue and at the counter. We know the arrival rate is 10 per hour, so customers must be spending 0.2
hours on average checking out.
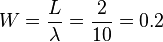
We can even apply Little's Law to the counter itself. The average number of people at the counter would be in the range (0, 1) since no more than one person can be at the counter at a time. In that case, the average number of people at the counter is also known
as the utilisation of the counter.
However, because a store in reality generally has a limited amount of space, it cannot become unstable. Even if the arrival rate is much greater than the exit rate, the store will eventually start to overflow, and thus any new arriving customers will simply
be rejected (and forced to go somewhere else or try again later) until there is once again free space available in the store. This is also the difference between the arrival rate and the effective arrival rate, where the arrival rate roughly
corresponds to the rate of which customers arrive at the store, whereas the effective arrival rate corresponds to the rate of which customers enter the store. In a system with an infinite size and no loss, the two are however equal.
相关文章推荐
- 计算机系统性能的重要估计法则:little's law
- hdu 5135 Little Zu Chongzhi's Triangles(计算几何:三角形面积)
- Little Boy's Problem
- Technical Artist的不归路 —— 费茨定律(Fitts's Law)在UI设计中的使用
- Murphy's Law 译为"摩非定律"--可能是软件里面总有BUG的原因
- HDU 5024 Wang Xifeng's Little Plot (搜索)
- Little Zu Chongzhi's Triangles(计算几何加贪心)
- 软件开发与项目管理易理——布鲁克斯法则 ( Brook's Law )
- HDU 5135 Little Zu Chongzhi's Triangles
- HDU 5024 Wang Xifeng's Little Plot (bfs)
- hdu 5024 Wang Xifeng's Little Plot
- HDU 5135 Little Zu Chongzhi's Triangles(状态压缩dp)
- HDU 5135 Little Zu Chongzhi's Triangles(状态压缩dp+Vector)
- Codeforces 630 B. Moore's Law
- Amdahl's Law
- URAL 1800 Murphy's Law(物理判断题)
- hdoj 5125 Little Zu Chongzhi's Triangles【状态压缩dp】
- Zipf's Law(map容器)
- 【并发】Amdahl's Law 阿姆达尔定律
- hdu 5024 Wang Xifeng's Little Plot (dfs+暴力)
